第一章 算法初步复习 教案2

第一章
算法初步复习
教案
教学目的：
总结算法解题的一般思路，即算法分析(提炼问题的数学本质)——画出程序框图——按框图编写伪代码；通过本章学习增强解题的规范性．
教学重点：
在准确理解算法的基础上，掌握流程图的画法及判断；掌握伪代码的编写．
教学过程：
例1．阅读下列伪代码，并指出当时的计算结果：
(1)read
a，
b
(2)
read
a，
b
(3)
read
a，
b
X←a+b
a←a+b
a←a+b
y←a-b
b←a-b
b←a-b
a←(x+y)/2
a←(a+b)/2
a←(a-b)/2
b←(x-y)/2
b←(a-b)/2
b←(a+b)/2
Print
a，
b
Print
a，
b
Print
a，
b
a=____，b___
a=____，b___
a=____，b___
例2．写出用二分法求方程在区间内的一个近似解(误差不超过)的一个算法．
说明：此题主要再次强调算法的问题根本上是一个思维的问题以及算法语言的基本规则；如何通过语句的结构形式规范处理及简化问题，
从而增强解题的规范性．
流程图与伪代码
10
Rend
a，b，c
20
x0
←(a+b)/2
30
f(a)
←a3-a-1
40
f(x0)
←x03-x0-1
50
If
f(x0)=0
then
Goto
120
60
If
f(a)f(x0)<0
then
70
b
←x0
80
Else
90
a
←x0
100
End
if
110
If
|a-b|≧c
then
Goto
20
120
Print
x0
N
以上两例重点理解赋值语句，尤其是在循环结构中如何根据对变量的理解灵活赋值，从而用简炼的语句表示算法.
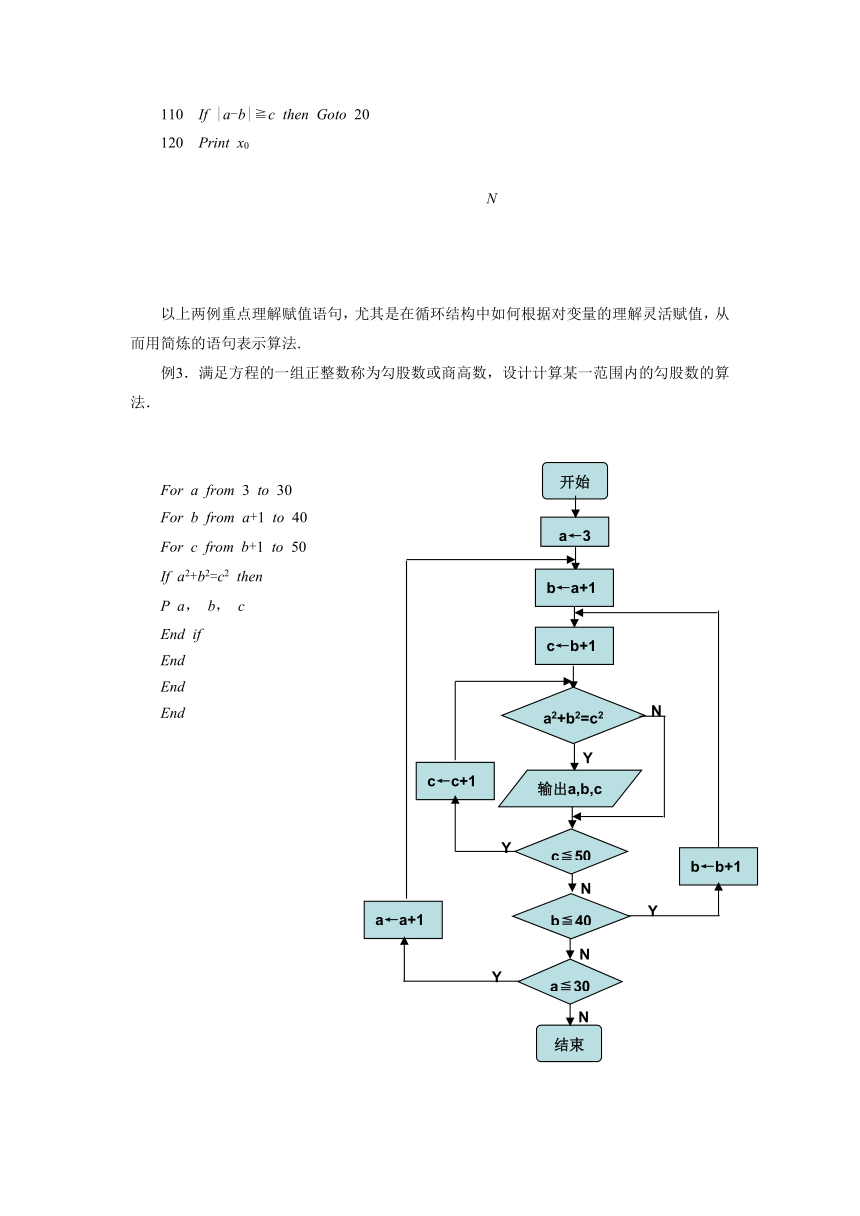
例3．满足方程的一组正整数称为勾股数或商高数，设计计算某一范围内的勾股数的算法．
For
a
from
3
to
30
For
b
from
a+1
to
40
For
c
from
b+1
to
50
If
a2+b2=c2
then
P
a，
b，
c
End
if
End
End
End
例四．已知钱数(不足10元)，要把它用于1元、5角、1角、1分的硬币表示，若要用尽量少的硬币个数表示，设计一个算法，求各硬币的个数．
分析：要用尽量少的硬币表示钱数，也就是要尽可能地用大面值的硬币．以1元钱的个数就是的整数部分，记为，则5角钱的个数就是(－)/0.5的整数部分，记为；1角钱的个数就是(－＊1－＊0.5)的整数部分，记为；1分钱的个数就是(－＊1－＊0.5－＊0.1)的整数部分．
解：Read
=int()
=int((－)/0.5)
=
int((－＊1－＊0.5)/0.1)
=int((－＊1－＊0.5－＊0.1)/0.01)
Print
，，，
例五.
在日常生活中，人们经常要把一些记录中的数据排序，如招生录取中按照成绩对考生进行排序，汉字拼音检索中按照字母顺序对汉字进行排序等等.排序就是按照一定的规则，对数据加以排列整理，从而提高查找效率．
(1)直接插入排序法：
(2)冒泡排序法：
现用直接插入排序法对任意输入的n个数进行从小到大的排序，其伪代码程序如下：
Begin
Read
n
For
i=1
to
n
Read
a(i)
End
For
For
i=2
to
n
For
j=1
to
i-1
If
a(j)>a(i)
Then
m=a(i)
a(i)=a(j)
a(j)=m
End
if
End
For
End
For
For
k=1
to
n
Print
a(k)
End
For
End
再用直接冒泡排序法对任意输入的n个数进行从小到大的排序，其伪代码程序如下：
10
Begin
20
Read
n
30
For
i=1
to
n
40
Read
a(i)
50
End
For
60
For
j=1
to
n-1
70
w=0
80
For
i=1
to
n-1
90
If
a(i)>a(i+1)
Then
100
m=a(i)
110
a(i)=a(i+1)
120
a(i+1)=m
130
w=w+1
140
end
if
150
End
For
160
If
w=0
Then
Goto
180
170
End
For
180
For
k=1
to
n
190
Print
a(k)
200
End
For
210
End
用DO循环语句表示如下：
Begin
Read
n
For
i=1
to
n
Read
a(i)
End
For
Do
w=0
For
i=1
to
n-1
If
a(i)>a(i+1)
Then
m=a(i)
a(i)=a(i+1)
a(i+1)=m
w=w+1
end
if
Next
i
Loop
Until
w=0
For
k=1
to
n
Print
a(k)
End
For
End
例三与例五及算经中的“百钱百鸡”问题均对循环语句的应用提出更高要求，在算法理解及流程图的设计上思路一定要清晰.
例六．(李白买酒)“无事街上走，提壶去买酒，遇店加一倍，见花喝一斗，三遇店和花，喝光壶中酒”．设计求酒壶中原有多少酒的一个算法并写出伪代码．
S=0
For
I
from
1
to
3
S←(S+1)/2
End
For
Pint
S
例七．一个三位数，如果每一位数字的立方和等于它本身，则称之为“水仙花数”．设计一个算法，找出所有的水仙花数，用伪代码表示．
For
n
from
100
to
999
←int(n/100)
←int((n-100x)/10)
z←n－100－10
If
n=3+3+z3
then
Pint
n
End
If
Next
n
End
for
例八．一辆邮车依次前往城市Ａ1，Ａ2，Ａ3，…Am()，每到一个城市先卸下前面各城市发往该城市的邮袋1个，然后再装上该城市发往后面各城市的邮袋各1个，
设ｎ是邮车从第ｎ个(1≤n＜m，n∈N
)城市出发时邮车上邮袋的个数，设计一个算法，对任给两个正数ｍ＞ｎ，求ｎ
分析:到达第n个城市时，邮袋个数为前一个城市的邮袋个数减去前面城市发往该市的n-1个邮袋，再加上发往后面各城市的(m-n)个邮袋，可用循环计算I从1至ｎ时，ｎ的变化.
解：　伪代码为：
Read
m，n
If
m≤n
then
Print“错误！ｍ必须大于ｎ”
Else
S←0
For
I
from
1
to
n
S←S+(m-
I)-(I-1)
Next
I
End
For
End
If
Print
S
例九．进位制与秦九韶算法
1．用程序把进制数(共有位)转换为十进制数
2．把一个十进制数化为k进制数
Begin
Read
a
，
k
i=1
Do
r=mod(a，k)
a(i)=r
a=(a-r)/k
i=i+1
Loop
Until
a=0
m=i-1
For
j=m
to
1
Step
-1
Print
a(j)；
Next
j
Prin
“(”；k；”)”
End
3．求次多项式当(是任意实数)的值
解析：把次多项式改写如下形式：
发现规律结合所掌握算法，通过模仿，操作，探索，寻找解决问题的通法.]
例十．(焚塔传说)
解析：关键是理解问题发现规律
输入a,b,c
输出x0
b←x0
a←x0
f(a)←a3-a-1
f(x0)←x03-x0-1
X0←(a+b)/2
|a-b|f(a)f(x0)<0
f(x0)=0
Y
N
Y
N
Y
N
N
N
a←3
输出a,b,c
b←a+1
Y
开始
结束
b←b+1
c←c+1
a←a+1
c←b+1
a≦30
b≦40
c≦50
a2+b2=c2
Y
Y
Y
N
Read
a,
k,
n
I=1
b=0
while
i<=n
t=get
a(i)
b=b+t
k︿(i-1)
i=i+1
end
while
print
b
输入f(x)的系数：
a0
a1
a2
…an
输入x0
I=1
I≦n
输出v
V=v0
V=v×x0+an-i
I=I+1
N
Y
开始
结束