1.1.2 条件结构 学案(含答案)
文档属性
| 名称 | 1.1.2 条件结构 学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-04 00:00:00 | ||
图片预览


文档简介
1.1.2
条件结构
学案
【学习目标】
1.了解条件结构的概念,并明确其执行过程.
2.会用条件结构设计程序框图解决有关问题.
【学习重点】
条件结构的执行过程.
课前预习案
【知识链接】
2015年元旦期间,某商品进行团购优惠活动:购买5件或5件以下,每件88元;超过5件,超过的部分按每件8折优惠.
1.若某人购买x件,试写出购物总费用y与购买件数x的关系式.
2.设计上述问题的算法时,应注意什么?
3.上述问题若画程序框图,只用顺序结构能完成吗?
【知识梳理】
条件结构
(1)概念:算法的流程根据条件是否成立有不同的____,这种处理________的结构称为条件结构.
(2)程序框图:如图①②所示.
小结:
(1)条件结构是程序框图的重要组成部分.其特点是先判断后执行.
2 在利用条件结构画程序框图时要注意两点:一是需要判断的条件是什么,二是条件判断后分别对应着什么样的结果.
3 判断框虽然有两个出口,但根据条件是否成立,选择的出口是确定的,故执行结果也是唯一的.如上面图①中,若条件成立,则执行步骤A,若条件不成立,则执行步骤B;图②中,若条件成立,则执行步骤A,若条件不成立,则不执行任何步骤.
4 凡是必须先根据条件作出判断然后再进行哪一个步骤的问题,在画程序框图时,必须引入一个判断框并应用条件结构.
对条件结构的理解
说明:可以从以下几方面来理解:
(1)条件结构有一个入口和两个出口;
(2)每执行一次条件结构,只能执行两个出口中的一个,不能同时执行两个出口;
(3)根据是否满足条件来确定执行哪个出口,满足条件执行一个出口,不满足条件执行另一个出口.
(4)对于算法中含有分类讨论的步骤,在设计程序框图时,通常用条件结构来解决.
例如,给出如图所示的程序框图,
若输入m=-2,则m>0不成立,此时执行ω=-2-1=-3,则输出-3.
若输入m=3,则m>0成立,此时执行ω=3+1=4,则输出4.
自主小测
1、
判断整数n是否是偶数,设计程序框图时所含有的基本逻辑结构是( )
A.顺序结构
B.条件结构
C.顺序结构、条件结构
D.以上都不正确
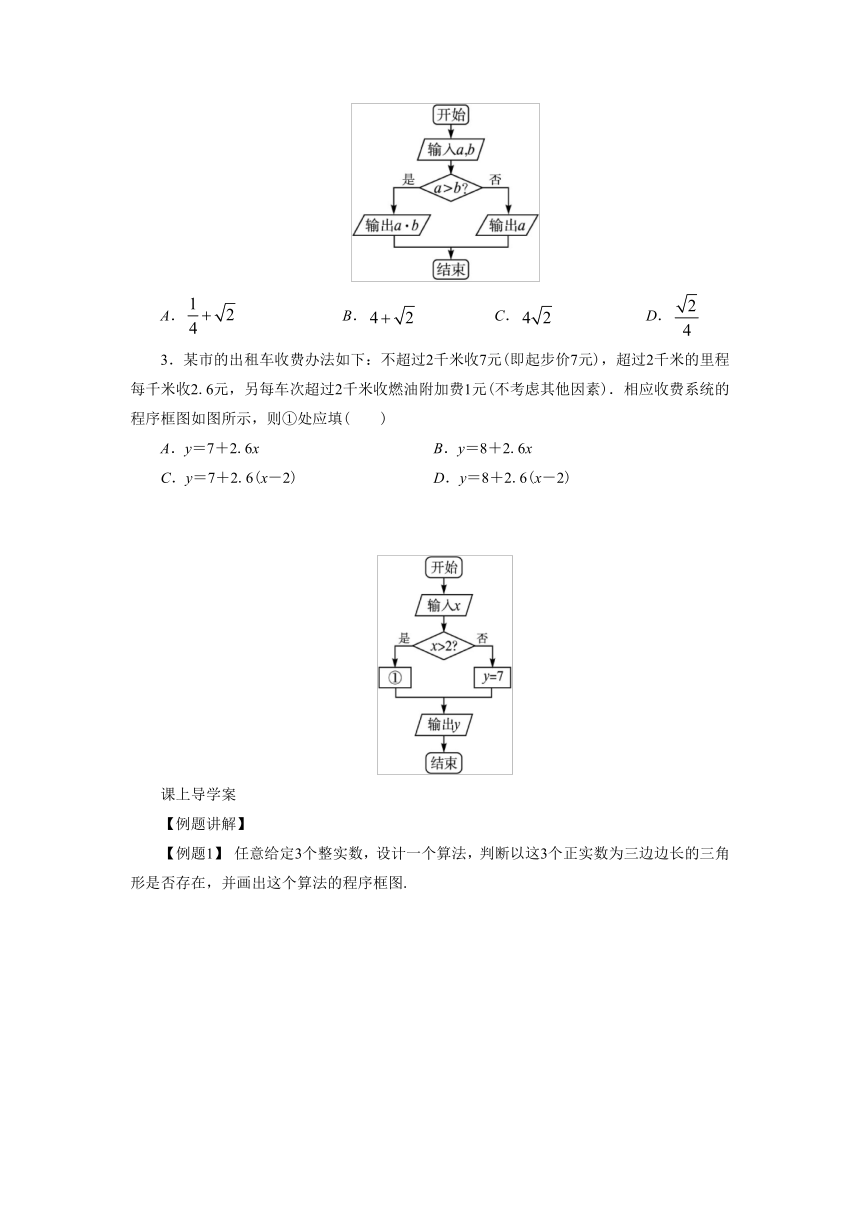
2、知a=,b=,运算原理如图所示,则输出的值为( )
A.
B.
C.
D.
3.某市的出租车收费办法如下:不超过2千米收7元(即起步价7元),超过2千米的里程每千米收2.6元,另每车次超过2千米收燃油附加费1元(不考虑其他因素).相应收费系统的程序框图如图所示,则①处应填( )
A.y=7+2.6x
B.y=8+2.6x
C.y=7+2.6(x-2)
D.y=8+2.6(x-2)
课上导学案
【例题讲解】
【例题1】
任意给定3个整实数,设计一个算法,判断以这3个正实数为三边边长的三角形是否存在,并画出这个算法的程序框图.
【例题2】设计一个求解一元二次方程的算法,并画出程序框图表示.
【当堂检测】
1.如图是计算函数y=的值的程序框图,在①②③处应分别填入的是( )
A.y=ln(-x),y=0,y=2x
B.y=ln(-x),y=2x,y=0
C.y=0,y=2x,y=ln(-x)
D.y=0,y=ln(-x),y=2x
2.如图是求某个函数的函数值的程序框图,则满足该程序框图的函数的解析式为__________.
【问题与收获】
【知识链接】答案:
1、【提示】 y=
2、【提示】 注意判断购买的件数对购物费用的影响.
3、【提示】 不能.
知识梳理答案:
(1)流向 判断条件
【做一做】
C 任何程序框图中都有顺序结构.当n能被2整除时,n是偶数;否则,n不是偶数,所以必须用条件结构来解决.
自主小测答案:1.D 因为a=>b==,所以a>b成立,所以输出a·b==.
2.D 当x>2时,y=7+2.6(x-2)+1=8+2.6(x-2),所以①处应填y=8+2.
6(x-2).
3.B 当x>-2不成立时,有x≤-2,则y=ln(-x),则①处填入y=ln(-x);当x>-2成立时,若x>3成立,则y=2x,则②处填入y=2x;若x>3不成立,即-2<x≤3,则y=0,则③处填入y=0.
例题答案:见教材(略)
当堂检测答案:
1.f(x)= 当满足x<0时,f(x)=2x-3;当不满足x<0,即x≥0时,f(x)=5-4x,所以满足该程序的函数解析式为f(x)=
2.分析:题中当n是奇数和n是偶数时的计算方式不同,所以需对n的奇偶性加以判断,然后计算结果.
解:算法步骤如下:
第一步,输入n的值.
第二步,若n为奇数,计算w=3n+1的值;否则,计算w=的值.
第三步,输出w.
程序框图如图所示.
条件结构
学案
【学习目标】
1.了解条件结构的概念,并明确其执行过程.
2.会用条件结构设计程序框图解决有关问题.
【学习重点】
条件结构的执行过程.
课前预习案
【知识链接】
2015年元旦期间,某商品进行团购优惠活动:购买5件或5件以下,每件88元;超过5件,超过的部分按每件8折优惠.
1.若某人购买x件,试写出购物总费用y与购买件数x的关系式.
2.设计上述问题的算法时,应注意什么?
3.上述问题若画程序框图,只用顺序结构能完成吗?
【知识梳理】
条件结构
(1)概念:算法的流程根据条件是否成立有不同的____,这种处理________的结构称为条件结构.
(2)程序框图:如图①②所示.
小结:
(1)条件结构是程序框图的重要组成部分.其特点是先判断后执行.
2 在利用条件结构画程序框图时要注意两点:一是需要判断的条件是什么,二是条件判断后分别对应着什么样的结果.
3 判断框虽然有两个出口,但根据条件是否成立,选择的出口是确定的,故执行结果也是唯一的.如上面图①中,若条件成立,则执行步骤A,若条件不成立,则执行步骤B;图②中,若条件成立,则执行步骤A,若条件不成立,则不执行任何步骤.
4 凡是必须先根据条件作出判断然后再进行哪一个步骤的问题,在画程序框图时,必须引入一个判断框并应用条件结构.
对条件结构的理解
说明:可以从以下几方面来理解:
(1)条件结构有一个入口和两个出口;
(2)每执行一次条件结构,只能执行两个出口中的一个,不能同时执行两个出口;
(3)根据是否满足条件来确定执行哪个出口,满足条件执行一个出口,不满足条件执行另一个出口.
(4)对于算法中含有分类讨论的步骤,在设计程序框图时,通常用条件结构来解决.
例如,给出如图所示的程序框图,
若输入m=-2,则m>0不成立,此时执行ω=-2-1=-3,则输出-3.
若输入m=3,则m>0成立,此时执行ω=3+1=4,则输出4.
自主小测
1、
判断整数n是否是偶数,设计程序框图时所含有的基本逻辑结构是( )
A.顺序结构
B.条件结构
C.顺序结构、条件结构
D.以上都不正确
2、知a=,b=,运算原理如图所示,则输出的值为( )
A.
B.
C.
D.
3.某市的出租车收费办法如下:不超过2千米收7元(即起步价7元),超过2千米的里程每千米收2.6元,另每车次超过2千米收燃油附加费1元(不考虑其他因素).相应收费系统的程序框图如图所示,则①处应填( )
A.y=7+2.6x
B.y=8+2.6x
C.y=7+2.6(x-2)
D.y=8+2.6(x-2)
课上导学案
【例题讲解】
【例题1】
任意给定3个整实数,设计一个算法,判断以这3个正实数为三边边长的三角形是否存在,并画出这个算法的程序框图.
【例题2】设计一个求解一元二次方程的算法,并画出程序框图表示.
【当堂检测】
1.如图是计算函数y=的值的程序框图,在①②③处应分别填入的是( )
A.y=ln(-x),y=0,y=2x
B.y=ln(-x),y=2x,y=0
C.y=0,y=2x,y=ln(-x)
D.y=0,y=ln(-x),y=2x
2.如图是求某个函数的函数值的程序框图,则满足该程序框图的函数的解析式为__________.
【问题与收获】
【知识链接】答案:
1、【提示】 y=
2、【提示】 注意判断购买的件数对购物费用的影响.
3、【提示】 不能.
知识梳理答案:
(1)流向 判断条件
【做一做】
C 任何程序框图中都有顺序结构.当n能被2整除时,n是偶数;否则,n不是偶数,所以必须用条件结构来解决.
自主小测答案:1.D 因为a=>b==,所以a>b成立,所以输出a·b==.
2.D 当x>2时,y=7+2.6(x-2)+1=8+2.6(x-2),所以①处应填y=8+2.
6(x-2).
3.B 当x>-2不成立时,有x≤-2,则y=ln(-x),则①处填入y=ln(-x);当x>-2成立时,若x>3成立,则y=2x,则②处填入y=2x;若x>3不成立,即-2<x≤3,则y=0,则③处填入y=0.
例题答案:见教材(略)
当堂检测答案:
1.f(x)= 当满足x<0时,f(x)=2x-3;当不满足x<0,即x≥0时,f(x)=5-4x,所以满足该程序的函数解析式为f(x)=
2.分析:题中当n是奇数和n是偶数时的计算方式不同,所以需对n的奇偶性加以判断,然后计算结果.
解:算法步骤如下:
第一步,输入n的值.
第二步,若n为奇数,计算w=3n+1的值;否则,计算w=的值.
第三步,输出w.
程序框图如图所示.
