1.2.2 条件语句 教案2
图片预览



文档简介
1.2.2
条件语句
教案
一、教材分析
通过上一节的学习,学生学会了输入语句、输出语句和赋值语句的基本用法,本节介绍条件语句的用法.
程序中的条件语句与程序框图中的条件结构存在一一对应关系,这种对应关系对于学生理解条件语句的结构,进一步理解算法中的条件结构都是很有帮助的.我们可以给出条件语句的一般格式,让学生自己画出相应的程序框图,也可以给出程序框图,让学生写出算法语句.
二、教学目标
1、知识与技能
(1)正确理解条件语句的概念,并掌握其结构的区别与联系.
(2)会应用条件语句编写程序.
2、过程与方法
经历对现实生活情境的探究,认识到应用计算机解决数学问题方便简捷,促进发展学生逻辑思维能力
3、情感态度与价值观
了解条件语句在程序中起判断转折作用,在解决实际问题中起决定作用.通过本小节内容的学习,有益于我们养成严谨的数学思维以及正确处理问题的能力.
三、重点难点
教学重点:条件语句的基本用法.
教学难点:算法语句的写法.
四、课时安排
1课时
五、教学设计
(一)导入新课
思路1(情境导入)
一位老农平整了一块良田,种瓜好呢,还是种豆好呢,他面临着一个选择.如果他选择种瓜,他会得瓜,如果他选择种豆,他会得豆.人的一生面临许多选择,我们要做出正确的选择.前面我们学习了条件结构,今天我们学习条件语句.
思路2(直接导入)
前面我们学习了程序框图的画法,为了让计算机能够理解算法步骤、程序框图,上一节我们学习了输入语句、输出语句、赋值语句,今天我们开始学习条件语句.
(二)推进新课、新知探究、提出问题
(1)回忆程序框图中的两种条件结构.
(2)指出条件语句的格式及功能.
(3)指出两种条件语句的相同点与不同点.
(4)揭示程序中的条件语句与程序框图中的条件结构存在一一对应关系.
讨论结果:
(1)一个算法中,经常会遇到一些条件的判断,算法的流程根据条件是否成立有不同的流向.条件结构就是处理这种过程的结构.
用程序框图表示条件结构如下图:
(2)条件语句
1°“IF—THEN—ELSE”语句
格式:
IF
条件
THEN
语句体1
ELSE
语句体2
END
IF
功能:在“IF—THEN—ELSE”语句中,“条件”表示判断的条件,“语句体1”表示满足条件时执行的操作内容;“语句体2”表示不满足条件时执行的操作内容;END
IF表示条件语句的结束.计算机在执行“IF—THEN—ELSE”语句时,首先对IF后的条件进行判断,如果符合条件,则执行THEN后面的“语句1”;若不符合条件,则执行ELSE后面的“语句2”.
2°“IF—THEN”语句
格式:
IF
条件
THEN
语句体
END
IF
功能:“条件”表示判断的条件;“语句”表示满足条件时执行的操作内容,条件不满足时,直接结束判断过程;END
IF表示条件语句的结束.计算机在执行“IF—THEN”语句时,首先对IF后的条件进行判断,如果符合条件就执行THEN后边的语句,若不符合条件则直接结束该条件语句,转而执行其他后面的语句.
(3)相同点:首先对IF后的条件进行判断,如果符合条件就执行THEN后边的语句.
不同点:对于“IF—THEN—ELSE”语句,若不符合条件,则执行ELSE后面的“语句体2”.
对于“IF—THEN”语句,若不符合条件则直接结束该条件语句,转而执行其他后面的语句.
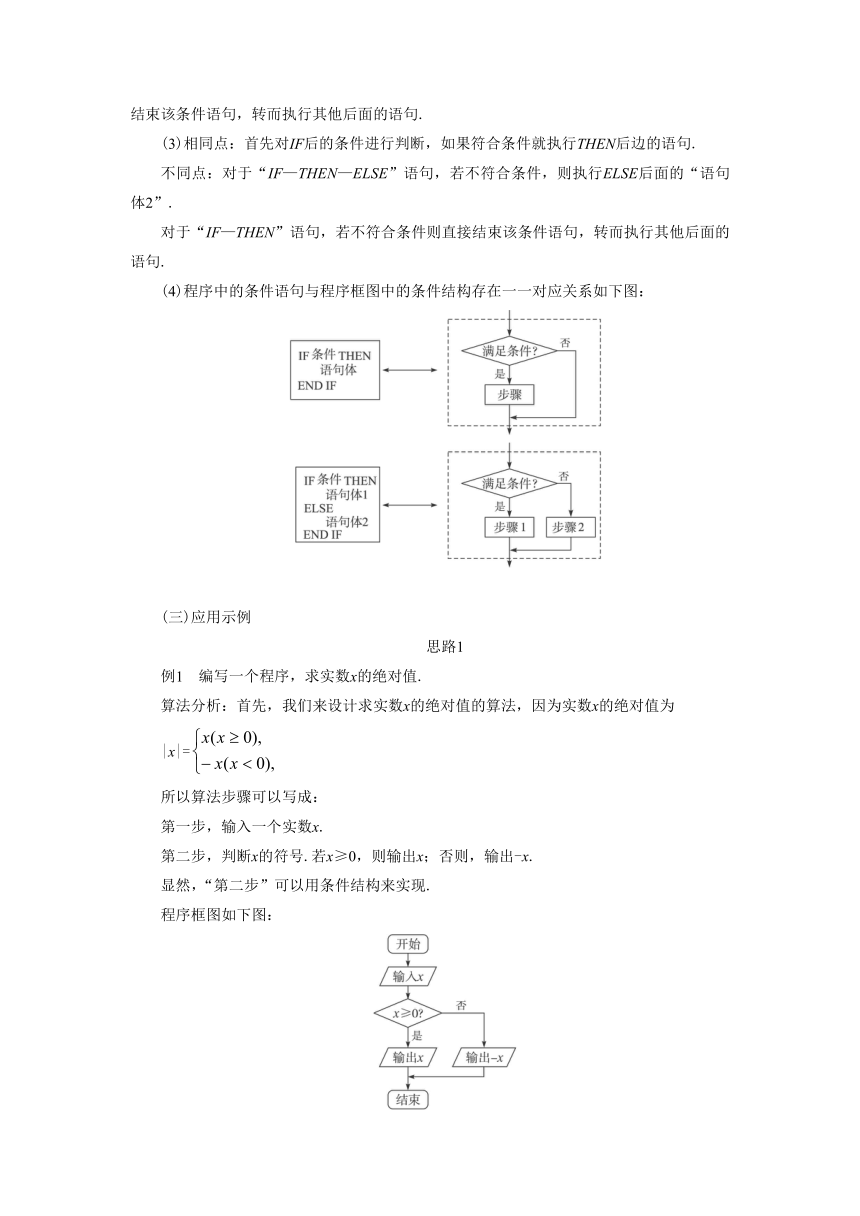
(4)程序中的条件语句与程序框图中的条件结构存在一一对应关系如下图:
(三)应用示例
思路1
例1
编写一个程序,求实数x的绝对值.
算法分析:首先,我们来设计求实数x的绝对值的算法,因为实数x的绝对值为
|x|=
所以算法步骤可以写成:
第一步,输入一个实数x.
第二步,判断x的符号.若x≥0,则输出x;否则,输出-x.
显然,“第二步”可以用条件结构来实现.
程序框图如下图:
程序:
INPUT
x
IF
x>=0
THEN
PRINT
x
ELSE
PRINT
-x
END
IF
END
点评:通过本题我们看到算法步骤可以转化为程序框图,程序框图可以转化为算法语句.本题揭示了它们之间的内在联系,只要理解了程序框图与算法语句的对应关系,把程序框图转化为算法语句就很容易了.
变式训练
阅读下面的程序,你能得出什么结论?
INPUT
x
IF
x<0
THEN
x=-x
END
IF
PRINT
x
END
解:由程序得出,该程序是输出x的绝对值.
例2
把前面求解一元二次方程ax2+bx+c=0的程序框图转化为程序.
解:由程序框图可以发现,其中包含着两个条件结构,而且内层的条件结构是外层的条件结构的一个分支,所以,可以用“IF—THEN—ELSE—END
IF”来完成转化.
程序:
INPUT
“a,b,c=”;a,b,c
d=b^2-4
a
c
IF
d>=0
THEN
p=-b/(2
a)
q=SQR(d)/(2
a)
IF
d=0
THEN
PRINT
“x1=x2=”;p
ELSE
PRINT
“x1,x2=”;p+q,p-q
END
IF
ELSE
PRINT“No
real
root”
END
IF
END
例3
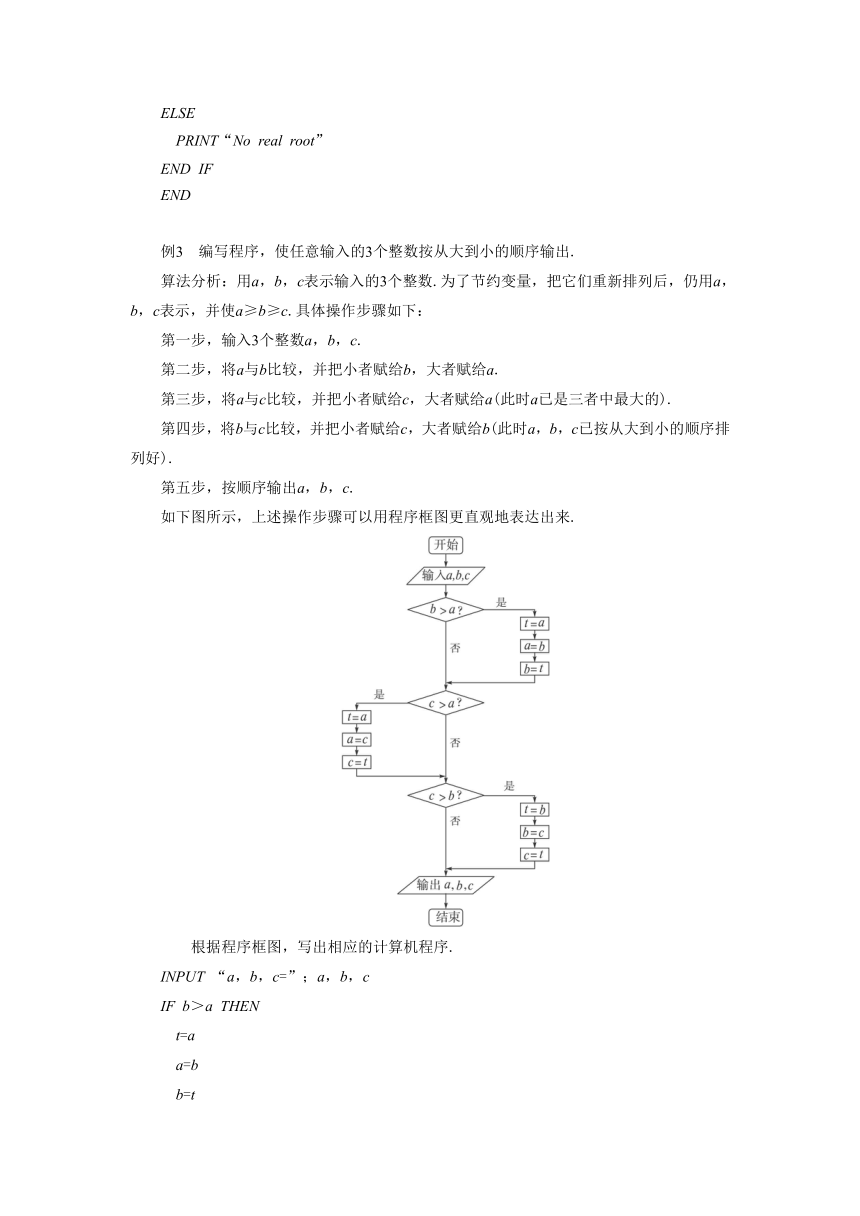
编写程序,使任意输入的3个整数按从大到小的顺序输出.
算法分析:用a,b,c表示输入的3个整数.为了节约变量,把它们重新排列后,仍用a,b,c表示,并使a≥b≥c.具体操作步骤如下:
第一步,输入3个整数a,b,c.
第二步,将a与b比较,并把小者赋给b,大者赋给a.
第三步,将a与c比较,并把小者赋给c,大者赋给a(此时a已是三者中最大的).
第四步,将b与c比较,并把小者赋给c,大者赋给b(此时a,b,c已按从大到小的顺序排列好).
第五步,按顺序输出a,b,c.
如下图所示,上述操作步骤可以用程序框图更直观地表达出来.
根据程序框图,写出相应的计算机程序.
INPUT
“a,b,c=”;a,b,c
IF
b>a
THEN
t=a
a=b
b=t
END
IF
IF
c>a
THEN
t=a
a=c
c=t
END
IF
IF
c>b
THEN
t=b
b=c
c=t
END
IF
PRINT
a,b,c
END
思路2
例1
编写程序,输出两个不相等的实数a、b的最大值.
分析:要输出两个不相等的实数a、b的最大值,从而想到对a,b的大小关系进行判断,a,b的大小关系有两种情况:(1)a>b;(2)b>a.这也就用到了我们经常提及的分类讨论的方式,找出两个数的最大值.
解:算法一:
第一步,输入a,
b的数值.
第二步,判断a,b的大小关系,若a>b,则输出a的值,否则,输出b的值.
(程序框图如下图)
程序如下:(“IF—THEN—ELSE”语句)
INPUT
“a,b”;a,b
IF
a>b
THEN
PRINT
a
ELSE
PRINT
b
END
IF
END
算法二:
第一步,输入a,b的数值.
第二步,判断a,b的大小关系,若b>a,则将b的值赋予a;否则,直接执行第三步.
第三步,输出a的值,结束.
(程序框图如下图)
程序如下:(“IF—THEN”语句)
INPUT
“a,b”;a,b
IF
b>a
THEN
a=b
END
IF
PRINT
a
END
点评:设计一个“好”的算法需要在大量的算法设计中积累经验.我们也可以先根据自己的思路设计算法,再与
“成形”的、高效的、优秀的算法比较,改进思路,改进算法,以避免重复计算等问题,提高算法设计的水平.
(2)我们在平常的训练中尽可能地少引用变量,过多的变量不仅会使得算法和程序变得复杂,而且不利于计算机的执行.为此,我们在练习中要尽可能少引入变量并且要积极思考才能少引入变量.
例2
高等数学中经常用到符号函数,符号函数的定义为y=试编写程序输入x的值,输出y的值.
解:程序一:(嵌套结构)
程序框图:(下图)
程序如下:
INPUT
x
IF
x>0
THEN
y=1
ELSE
IF
x=0
THEN
y=0
ELSE
y=-1
END
IF
END
IF
PRINT
y
END
程序二:(叠加结构)
程序框图(右图):
程序如下:
INPUT
x
IF
x>0
THEN
y=1
END
IF
IF
x=0
THEN
y=0
END
IF
IF
x<0
THEN
y=-1
END
IF
PRINT
y
END
点评:(1)条件结构的差异,造成程序执行的不同.当代入x的数值时,“程序一”先判断外层的条件,依次执行不同的分支,随后再判断内层的条件;而“程序二”中执行了对“条件1”的判断,同时也对“条件2”进行判断,是按程序中条件语句的先后依次判断所有的条件,满足哪个条件就执行哪个语句.
(2)条件语句的嵌套可多于两层,可以表达算法步骤中的多重限制条件.
(四)知能训练
中国网通规定:拨打市内电话时,如果不超过3分钟,则收取话费0.22元;如果通话时间超过3分钟,则超出部分按每分钟0.1元收取通话费,不足一分钟按以一分钟计算.设通话时间为t(分钟),通话费用y(元),如何设计一个程序,计算通话的费用.
解:算法程序如下:
INPUT
“请输入通话时间:”;t
IF
t<=3
THEN
y=0.22
ELSE
IF
INT(t)=t
THEN
y=0.22+0.1
(t-3)
ELSE
y=0.22+0.1
(INT(t-3)+1)
END
IF
END
IF
PRINT
“通话费用为:”;y
END
(五)拓展提升
函数y=写出求函数的函数值的程序.
解:INPUT
x=”;x
IF
x>=0
and
x<=4
THEN
y=2
x
ELSE
IF
x<=8
THEN
y=8
ELSE
y=2
(12-x)
END
IF
END
IF
PRINT
y
END
(六)课堂小结
(1)条件语句的用法.
(2)利用条件语句编写算法语句.
(七)作业
习题1.2
B组1.
条件语句
教案
一、教材分析
通过上一节的学习,学生学会了输入语句、输出语句和赋值语句的基本用法,本节介绍条件语句的用法.
程序中的条件语句与程序框图中的条件结构存在一一对应关系,这种对应关系对于学生理解条件语句的结构,进一步理解算法中的条件结构都是很有帮助的.我们可以给出条件语句的一般格式,让学生自己画出相应的程序框图,也可以给出程序框图,让学生写出算法语句.
二、教学目标
1、知识与技能
(1)正确理解条件语句的概念,并掌握其结构的区别与联系.
(2)会应用条件语句编写程序.
2、过程与方法
经历对现实生活情境的探究,认识到应用计算机解决数学问题方便简捷,促进发展学生逻辑思维能力
3、情感态度与价值观
了解条件语句在程序中起判断转折作用,在解决实际问题中起决定作用.通过本小节内容的学习,有益于我们养成严谨的数学思维以及正确处理问题的能力.
三、重点难点
教学重点:条件语句的基本用法.
教学难点:算法语句的写法.
四、课时安排
1课时
五、教学设计
(一)导入新课
思路1(情境导入)
一位老农平整了一块良田,种瓜好呢,还是种豆好呢,他面临着一个选择.如果他选择种瓜,他会得瓜,如果他选择种豆,他会得豆.人的一生面临许多选择,我们要做出正确的选择.前面我们学习了条件结构,今天我们学习条件语句.
思路2(直接导入)
前面我们学习了程序框图的画法,为了让计算机能够理解算法步骤、程序框图,上一节我们学习了输入语句、输出语句、赋值语句,今天我们开始学习条件语句.
(二)推进新课、新知探究、提出问题
(1)回忆程序框图中的两种条件结构.
(2)指出条件语句的格式及功能.
(3)指出两种条件语句的相同点与不同点.
(4)揭示程序中的条件语句与程序框图中的条件结构存在一一对应关系.
讨论结果:
(1)一个算法中,经常会遇到一些条件的判断,算法的流程根据条件是否成立有不同的流向.条件结构就是处理这种过程的结构.
用程序框图表示条件结构如下图:
(2)条件语句
1°“IF—THEN—ELSE”语句
格式:
IF
条件
THEN
语句体1
ELSE
语句体2
END
IF
功能:在“IF—THEN—ELSE”语句中,“条件”表示判断的条件,“语句体1”表示满足条件时执行的操作内容;“语句体2”表示不满足条件时执行的操作内容;END
IF表示条件语句的结束.计算机在执行“IF—THEN—ELSE”语句时,首先对IF后的条件进行判断,如果符合条件,则执行THEN后面的“语句1”;若不符合条件,则执行ELSE后面的“语句2”.
2°“IF—THEN”语句
格式:
IF
条件
THEN
语句体
END
IF
功能:“条件”表示判断的条件;“语句”表示满足条件时执行的操作内容,条件不满足时,直接结束判断过程;END
IF表示条件语句的结束.计算机在执行“IF—THEN”语句时,首先对IF后的条件进行判断,如果符合条件就执行THEN后边的语句,若不符合条件则直接结束该条件语句,转而执行其他后面的语句.
(3)相同点:首先对IF后的条件进行判断,如果符合条件就执行THEN后边的语句.
不同点:对于“IF—THEN—ELSE”语句,若不符合条件,则执行ELSE后面的“语句体2”.
对于“IF—THEN”语句,若不符合条件则直接结束该条件语句,转而执行其他后面的语句.
(4)程序中的条件语句与程序框图中的条件结构存在一一对应关系如下图:
(三)应用示例
思路1
例1
编写一个程序,求实数x的绝对值.
算法分析:首先,我们来设计求实数x的绝对值的算法,因为实数x的绝对值为
|x|=
所以算法步骤可以写成:
第一步,输入一个实数x.
第二步,判断x的符号.若x≥0,则输出x;否则,输出-x.
显然,“第二步”可以用条件结构来实现.
程序框图如下图:
程序:
INPUT
x
IF
x>=0
THEN
x
ELSE
-x
END
IF
END
点评:通过本题我们看到算法步骤可以转化为程序框图,程序框图可以转化为算法语句.本题揭示了它们之间的内在联系,只要理解了程序框图与算法语句的对应关系,把程序框图转化为算法语句就很容易了.
变式训练
阅读下面的程序,你能得出什么结论?
INPUT
x
IF
x<0
THEN
x=-x
END
IF
x
END
解:由程序得出,该程序是输出x的绝对值.
例2
把前面求解一元二次方程ax2+bx+c=0的程序框图转化为程序.
解:由程序框图可以发现,其中包含着两个条件结构,而且内层的条件结构是外层的条件结构的一个分支,所以,可以用“IF—THEN—ELSE—END
IF”来完成转化.
程序:
INPUT
“a,b,c=”;a,b,c
d=b^2-4
a
c
IF
d>=0
THEN
p=-b/(2
a)
q=SQR(d)/(2
a)
IF
d=0
THEN
“x1=x2=”;p
ELSE
“x1,x2=”;p+q,p-q
END
IF
ELSE
PRINT“No
real
root”
END
IF
END
例3
编写程序,使任意输入的3个整数按从大到小的顺序输出.
算法分析:用a,b,c表示输入的3个整数.为了节约变量,把它们重新排列后,仍用a,b,c表示,并使a≥b≥c.具体操作步骤如下:
第一步,输入3个整数a,b,c.
第二步,将a与b比较,并把小者赋给b,大者赋给a.
第三步,将a与c比较,并把小者赋给c,大者赋给a(此时a已是三者中最大的).
第四步,将b与c比较,并把小者赋给c,大者赋给b(此时a,b,c已按从大到小的顺序排列好).
第五步,按顺序输出a,b,c.
如下图所示,上述操作步骤可以用程序框图更直观地表达出来.
根据程序框图,写出相应的计算机程序.
INPUT
“a,b,c=”;a,b,c
IF
b>a
THEN
t=a
a=b
b=t
END
IF
IF
c>a
THEN
t=a
a=c
c=t
END
IF
IF
c>b
THEN
t=b
b=c
c=t
END
IF
a,b,c
END
思路2
例1
编写程序,输出两个不相等的实数a、b的最大值.
分析:要输出两个不相等的实数a、b的最大值,从而想到对a,b的大小关系进行判断,a,b的大小关系有两种情况:(1)a>b;(2)b>a.这也就用到了我们经常提及的分类讨论的方式,找出两个数的最大值.
解:算法一:
第一步,输入a,
b的数值.
第二步,判断a,b的大小关系,若a>b,则输出a的值,否则,输出b的值.
(程序框图如下图)
程序如下:(“IF—THEN—ELSE”语句)
INPUT
“a,b”;a,b
IF
a>b
THEN
a
ELSE
b
END
IF
END
算法二:
第一步,输入a,b的数值.
第二步,判断a,b的大小关系,若b>a,则将b的值赋予a;否则,直接执行第三步.
第三步,输出a的值,结束.
(程序框图如下图)
程序如下:(“IF—THEN”语句)
INPUT
“a,b”;a,b
IF
b>a
THEN
a=b
END
IF
a
END
点评:设计一个“好”的算法需要在大量的算法设计中积累经验.我们也可以先根据自己的思路设计算法,再与
“成形”的、高效的、优秀的算法比较,改进思路,改进算法,以避免重复计算等问题,提高算法设计的水平.
(2)我们在平常的训练中尽可能地少引用变量,过多的变量不仅会使得算法和程序变得复杂,而且不利于计算机的执行.为此,我们在练习中要尽可能少引入变量并且要积极思考才能少引入变量.
例2
高等数学中经常用到符号函数,符号函数的定义为y=试编写程序输入x的值,输出y的值.
解:程序一:(嵌套结构)
程序框图:(下图)
程序如下:
INPUT
x
IF
x>0
THEN
y=1
ELSE
IF
x=0
THEN
y=0
ELSE
y=-1
END
IF
END
IF
y
END
程序二:(叠加结构)
程序框图(右图):
程序如下:
INPUT
x
IF
x>0
THEN
y=1
END
IF
IF
x=0
THEN
y=0
END
IF
IF
x<0
THEN
y=-1
END
IF
y
END
点评:(1)条件结构的差异,造成程序执行的不同.当代入x的数值时,“程序一”先判断外层的条件,依次执行不同的分支,随后再判断内层的条件;而“程序二”中执行了对“条件1”的判断,同时也对“条件2”进行判断,是按程序中条件语句的先后依次判断所有的条件,满足哪个条件就执行哪个语句.
(2)条件语句的嵌套可多于两层,可以表达算法步骤中的多重限制条件.
(四)知能训练
中国网通规定:拨打市内电话时,如果不超过3分钟,则收取话费0.22元;如果通话时间超过3分钟,则超出部分按每分钟0.1元收取通话费,不足一分钟按以一分钟计算.设通话时间为t(分钟),通话费用y(元),如何设计一个程序,计算通话的费用.
解:算法程序如下:
INPUT
“请输入通话时间:”;t
IF
t<=3
THEN
y=0.22
ELSE
IF
INT(t)=t
THEN
y=0.22+0.1
(t-3)
ELSE
y=0.22+0.1
(INT(t-3)+1)
END
IF
END
IF
“通话费用为:”;y
END
(五)拓展提升
函数y=写出求函数的函数值的程序.
解:INPUT
x=”;x
IF
x>=0
and
x<=4
THEN
y=2
x
ELSE
IF
x<=8
THEN
y=8
ELSE
y=2
(12-x)
END
IF
END
IF
y
END
(六)课堂小结
(1)条件语句的用法.
(2)利用条件语句编写算法语句.
(七)作业
习题1.2
B组1.
