5.2 平行四边形的性质和判定 练习题(含答案)
文档属性
| 名称 | 5.2 平行四边形的性质和判定 练习题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 135.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-03 00:00:00 | ||
图片预览


文档简介
鲁教版初三数学上册第五单元平行四边形的性质和判定练习题(含答案)
一.选择题(共12小题)
1.如图,在平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的大小为( )
A.150°
B.130°
C.120°
D.100°
(1题图)
(2题图)
(3题图)
2.如图,平行四边形ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为( )
A.3cm
B.4cm
C.5cm
D.8cm
3.如图, ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )
A.13
B.17
C.20
D.26
4.如图,将 ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为( )
A.66°
B.104°
C.114°
D.124°
(4题图)
(5题图)
(6题图)
5.如图,在 ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )
A.8
B.10
C.12
D.14
6.如图,在 ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于( )
A.2
B.3
C.4
D.6
7.下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
8.下列条件中,不能判断四边形ABCD是平行四边形的为( )
A.AB∥CD,AD∥BC
B.AB=CD,AD=BC
C.AB∥CD,AD=BC
D.AB∥CD,AB=CD
9.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,给出下列四个条件:①AE=CF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )
A.0个
B.1个
C.2个
D.3个
(9题图)
(12题图)
(13题图)
10.能判定四边形ABCD是平行四边形的条件是:∠A:∠B:∠C:∠D的值为( )
A.1:2:3:4
B.1:4:2:3
C.1:2:2:1
D.1:2:1:2
11.图①、图②、图③分别表示甲、乙、丙三人由A地到B地的路线图(箭头表示行进的方向).图②中E为AB的中点,图③中AJ>JB.判断三人行进路线长度的大小关系为( )
A.甲=乙=丙
B.甲<乙<丙
C.乙<丙<甲
D.丙<乙<甲
12.如图,在 ABCD中,EF∥AD,HN∥AB,则图中的平行四边形(不包括四边形ABCD)的个数共有( )
A.9个
B.8个
C.6个
D.4个
二.填空题(共7小题)
13.如图,在 ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为 .
14.如图所示,在 ABCD中,∠C=40°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为 .
(14题图)
(15题图)
(16题图)
15.如图,若 ABCD的面积为20,BC=5,则边AD与BC间的距离为 .
16.如图,把平行四边形ABCD折叠,使点C与点A重合,这时点D落在D1,折痕为EF,若∠BAE=55°,则∠D1AD= .
17.已知直角坐标系内有四个点O(0,0),A(3,0),B(1,1),C(x,1),若以O,A,B,C为顶点的四边形是平行四边形,则x= .
18.如图,四边形ABCD的对角线交于点O,从下列条件:①AD∥BC,②AB=CD,③AO=CO,④∠ABC=∠ADC中选出两个可使四边形ABCD是平行四边形,则你选的两个条件是 .(填写一组序号即可)
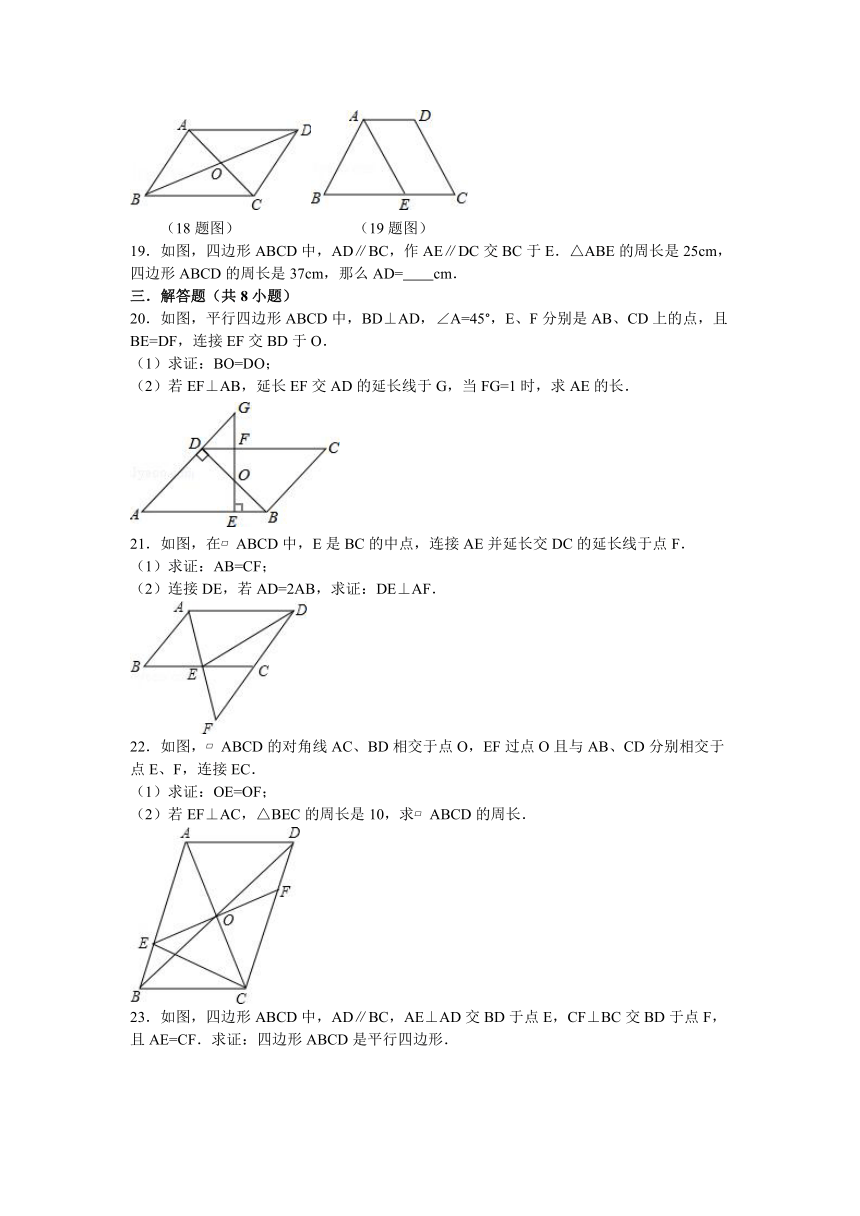
(18题图)
(19题图)
19.如图,四边形ABCD中,AD∥BC,作AE∥DC交BC于E.△ABE的周长是25cm,四边形ABCD的周长是37cm,那么AD= cm.
三.解答题(共8小题)
20.如图,平行四边形ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AE的长.
21.如图,在 ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
22.如图, ABCD的对角线AC、BD相交于点O,EF过点O且与AB、CD分别相交于点E、F,连接EC.
(1)求证:OE=OF;
(2)若EF⊥AC,△BEC的周长是10,求 ABCD的周长.
23.如图,四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF.求证:四边形ABCD是平行四边形.
24.如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
25.如图,在 ABCD中,点E,F在对角线AC上,且AE=CF.求证:
(1)DE=BF;
(2)四边形DEBF是平行四边形.
26.如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,EF∥AC.求证:BE=CF.
27.如图,已知点A、C在EF上,AD∥BC,DE∥BF,AE=CF.
(1)求证:四边形ABCD是平行四边形;
(2)直接写出图中所有相等的线段(AE=CF除外).
鲁教版初三数学上册第五单元平行四边形的性质和判定练习题参考答案
一.选择题(共12小题)
1.C.
2.B.解:∵ ABCD的周长为26cm,∴AB+AD=13cm,OB=OD,
∵△AOD的周长比△AOB的周长多3cm,
∴(OA+OB+AD)﹣(OA+OD+AB)=AD﹣AB=3cm,
∴AB=5cm,AD=8cm.∴BC=AD=8cm.
∵AC⊥AB,E是BC中点,∴AE=BC=4cm;故选:B.
3.B.
4.C.解:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠ACD=∠BAC,
由折叠的性质得:∠BAC=∠B′AC,∴∠BAC=∠ACD=∠B′AC=∠1=22°,
∴∠B=180°﹣∠2﹣∠BAC=180°﹣44°﹣22°=114°;故选:C.
5.B. 6.C.7.D.8.C.9.B.10.D.
11.A.解:图1中:甲走的路线长是:AC+BC;
图②中:延长AD和BF交于C.
∵∠DAE=∠FEB=40°,∴AD∥EF,则DC∥EF.同理EF∥CD,
∴四边形CDEF是平行四边形,∴EF=CD,DE=CF,
即乙走的路线长是:AD+DE+EF+FB=AD+CD+CF+BC=AC+BC;
图③中,延长AI和BK交于C.
与以上证明过程类似IC=JK,CK=IJ,
即丙走的路线长是AI+IJ+JK+KB=AI+CK+IC+BK=AC+BC;即甲=乙=丙,故选:A.
12.A.解:设EF与NH交于点O,
∵在 ABCD中,EF∥AD,HN∥AB,∴AD∥EF∥BC,AB∥NH∥CD,
则图中的四边BEOH、DEFC、DHGA、BGOF、BGHC、BAEF、AGOE、CHOF和ABCD都是平行四边形,共9个.
故选A.
二.填空题(共7小题)
13. 110° .14. 50° .15. 4 . 16. 55° .
17. 4或﹣2 .解:根据题意画图如下:
以O,A,B,C为顶点的四边形是平行四边形,则C(4,1)或(﹣2,1),
则x=4或﹣2;
故答案为:4或﹣2.
18. ①③ .
19. 12 .
三.解答题(共8小题)
20.(1)证明:∵四边形ABCD是平行四边形,∴DC∥AB,∴∠OBE=∠ODF.
在△OBE与△ODF中,∴△OBE≌△ODF(AAS).∴BO=DO.
(2)解:∵EF⊥AB,AB∥DC,∴∠GEA=∠GFD=90°.
∵∠A=45°,∴∠G=∠A=45°.
∴AE=GE
∵BD⊥AD,∴∠ADB=∠GDO=90°.∴∠GOD=∠G=45°.∴DG=DO,∴OF=FG=1,
由(1)可知,OE=OF=1,∴GE=OE+OF+FG=3,∴AE=3.
21.证明:(1)∵四边形ABCD是平行四边形,∴AB∥DF,∴∠ABE=∠FCE,
∵E为BC中点,∴BE=CE,
在△ABE与△FCE中,,∴△ABE≌△FCE(ASA),∴AB=FC;
(2)∵AD=2AB,AB=FC=CD,∴AD=DF,
∵△ABE≌△FCE,∴AE=EF,∴DE⊥AF.
22.(1)证明:∵四边形ABCD是平行四边形,∴OD=OB,DC∥AB,∴∠FDO=∠EBO,
在△DFO和△BEO中,,∴△DFO≌△BEO(ASA),∴OE=OF.
(2)解:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,OA=OC,
∵EF⊥AC,∴AE=CE,
∵△BEC的周长是10,∴BC+BE+CE=BC+BE+AE=BC+AB=10,
∴ ABCD的周长=2(BC+AB)=20.
23.证明:∵AE⊥AD,CF⊥BC,∴∠EAD=∠FCB=90°,
∵AD∥BC,∴∠ADE=∠CBF,
在Rt△AED和Rt△CFB中,∵,∴Rt△AED≌Rt△CFB(AAS),
∴AD=BC,
∵AD∥BC,∴四边形ABCD是平行四边形.
24.证明:(1)∵Rt△ABC中,∠BAC=30°,∴AB=2BC,
又∵△ABE是等边三角形,EF⊥AB,∴AB=2AF∴AF=BC,
在Rt△AFE和Rt△BCA中,
,∴Rt△AFE≌Rt△BCA(HL),∴AC=EF;
(2)∵△ACD是等边三角形,∴∠DAC=60°,AC=AD,∴∠DAB=∠DAC+∠BAC=90°
又∵EF⊥AB,∴EF∥AD,
∵AC=EF,AC=AD,∴EF=AD,
∴四边形ADFE是平行四边形.
25.证明:(1)∵四边形ABCD是平行四边形,∴AD∥CB,AD=CB,∴∠DAE=∠BCF,
在△ADE和△CBF中,∴△ADE≌△CBF,∴DE=BF.
(2)由(1),可得△ADE≌△CBF,∴∠ADE=∠CBF,
∵∠DEF=∠DAE+∠ADE,∠BFE=∠BCF+∠CBF,∴∠DEF=∠BFE,∴DE∥BF,
又∵DE=BF,
∴四边形DEBF是平行四边形.
26.证明:∵ED∥BC,EF∥AC,∴四边形EFCD是平行四边形,∴DE=CF,
∵BD平分∠ABC,∴∠EBD=∠DBC,
∵DE∥BC,∴∠EDB=∠DBC,∴∠EBD=∠EDB,∴EB=ED,
∴EB=CF.
27.(1)证明:∵AD∥BC,DE∥BF,∴∠E=∠F,∠DAC=∠BCA,∴∠DAE=∠BCF,
在△ADE和△CBF中,,∴△ADE≌△CBF(ASA),∴AD=CB,
∴四边形ABCD是平行四边形;
(2)解:AD=BC、EC=AF、ED=BF、AB=DC;理由如下:
∵△ADE≌△CBF,∴AD=BC,ED=BF,
∵AE=CF,∴EC=AF,∵四边形ABCD是平行四边形,∴AB=DC.
一.选择题(共12小题)
1.如图,在平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的大小为( )
A.150°
B.130°
C.120°
D.100°
(1题图)
(2题图)
(3题图)
2.如图,平行四边形ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为( )
A.3cm
B.4cm
C.5cm
D.8cm
3.如图, ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )
A.13
B.17
C.20
D.26
4.如图,将 ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为( )
A.66°
B.104°
C.114°
D.124°
(4题图)
(5题图)
(6题图)
5.如图,在 ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )
A.8
B.10
C.12
D.14
6.如图,在 ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于( )
A.2
B.3
C.4
D.6
7.下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
8.下列条件中,不能判断四边形ABCD是平行四边形的为( )
A.AB∥CD,AD∥BC
B.AB=CD,AD=BC
C.AB∥CD,AD=BC
D.AB∥CD,AB=CD
9.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,给出下列四个条件:①AE=CF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )
A.0个
B.1个
C.2个
D.3个
(9题图)
(12题图)
(13题图)
10.能判定四边形ABCD是平行四边形的条件是:∠A:∠B:∠C:∠D的值为( )
A.1:2:3:4
B.1:4:2:3
C.1:2:2:1
D.1:2:1:2
11.图①、图②、图③分别表示甲、乙、丙三人由A地到B地的路线图(箭头表示行进的方向).图②中E为AB的中点,图③中AJ>JB.判断三人行进路线长度的大小关系为( )
A.甲=乙=丙
B.甲<乙<丙
C.乙<丙<甲
D.丙<乙<甲
12.如图,在 ABCD中,EF∥AD,HN∥AB,则图中的平行四边形(不包括四边形ABCD)的个数共有( )
A.9个
B.8个
C.6个
D.4个
二.填空题(共7小题)
13.如图,在 ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为 .
14.如图所示,在 ABCD中,∠C=40°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为 .
(14题图)
(15题图)
(16题图)
15.如图,若 ABCD的面积为20,BC=5,则边AD与BC间的距离为 .
16.如图,把平行四边形ABCD折叠,使点C与点A重合,这时点D落在D1,折痕为EF,若∠BAE=55°,则∠D1AD= .
17.已知直角坐标系内有四个点O(0,0),A(3,0),B(1,1),C(x,1),若以O,A,B,C为顶点的四边形是平行四边形,则x= .
18.如图,四边形ABCD的对角线交于点O,从下列条件:①AD∥BC,②AB=CD,③AO=CO,④∠ABC=∠ADC中选出两个可使四边形ABCD是平行四边形,则你选的两个条件是 .(填写一组序号即可)
(18题图)
(19题图)
19.如图,四边形ABCD中,AD∥BC,作AE∥DC交BC于E.△ABE的周长是25cm,四边形ABCD的周长是37cm,那么AD= cm.
三.解答题(共8小题)
20.如图,平行四边形ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AE的长.
21.如图,在 ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
22.如图, ABCD的对角线AC、BD相交于点O,EF过点O且与AB、CD分别相交于点E、F,连接EC.
(1)求证:OE=OF;
(2)若EF⊥AC,△BEC的周长是10,求 ABCD的周长.
23.如图,四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF.求证:四边形ABCD是平行四边形.
24.如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
25.如图,在 ABCD中,点E,F在对角线AC上,且AE=CF.求证:
(1)DE=BF;
(2)四边形DEBF是平行四边形.
26.如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,EF∥AC.求证:BE=CF.
27.如图,已知点A、C在EF上,AD∥BC,DE∥BF,AE=CF.
(1)求证:四边形ABCD是平行四边形;
(2)直接写出图中所有相等的线段(AE=CF除外).
鲁教版初三数学上册第五单元平行四边形的性质和判定练习题参考答案
一.选择题(共12小题)
1.C.
2.B.解:∵ ABCD的周长为26cm,∴AB+AD=13cm,OB=OD,
∵△AOD的周长比△AOB的周长多3cm,
∴(OA+OB+AD)﹣(OA+OD+AB)=AD﹣AB=3cm,
∴AB=5cm,AD=8cm.∴BC=AD=8cm.
∵AC⊥AB,E是BC中点,∴AE=BC=4cm;故选:B.
3.B.
4.C.解:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠ACD=∠BAC,
由折叠的性质得:∠BAC=∠B′AC,∴∠BAC=∠ACD=∠B′AC=∠1=22°,
∴∠B=180°﹣∠2﹣∠BAC=180°﹣44°﹣22°=114°;故选:C.
5.B. 6.C.7.D.8.C.9.B.10.D.
11.A.解:图1中:甲走的路线长是:AC+BC;
图②中:延长AD和BF交于C.
∵∠DAE=∠FEB=40°,∴AD∥EF,则DC∥EF.同理EF∥CD,
∴四边形CDEF是平行四边形,∴EF=CD,DE=CF,
即乙走的路线长是:AD+DE+EF+FB=AD+CD+CF+BC=AC+BC;
图③中,延长AI和BK交于C.
与以上证明过程类似IC=JK,CK=IJ,
即丙走的路线长是AI+IJ+JK+KB=AI+CK+IC+BK=AC+BC;即甲=乙=丙,故选:A.
12.A.解:设EF与NH交于点O,
∵在 ABCD中,EF∥AD,HN∥AB,∴AD∥EF∥BC,AB∥NH∥CD,
则图中的四边BEOH、DEFC、DHGA、BGOF、BGHC、BAEF、AGOE、CHOF和ABCD都是平行四边形,共9个.
故选A.
二.填空题(共7小题)
13. 110° .14. 50° .15. 4 . 16. 55° .
17. 4或﹣2 .解:根据题意画图如下:
以O,A,B,C为顶点的四边形是平行四边形,则C(4,1)或(﹣2,1),
则x=4或﹣2;
故答案为:4或﹣2.
18. ①③ .
19. 12 .
三.解答题(共8小题)
20.(1)证明:∵四边形ABCD是平行四边形,∴DC∥AB,∴∠OBE=∠ODF.
在△OBE与△ODF中,∴△OBE≌△ODF(AAS).∴BO=DO.
(2)解:∵EF⊥AB,AB∥DC,∴∠GEA=∠GFD=90°.
∵∠A=45°,∴∠G=∠A=45°.
∴AE=GE
∵BD⊥AD,∴∠ADB=∠GDO=90°.∴∠GOD=∠G=45°.∴DG=DO,∴OF=FG=1,
由(1)可知,OE=OF=1,∴GE=OE+OF+FG=3,∴AE=3.
21.证明:(1)∵四边形ABCD是平行四边形,∴AB∥DF,∴∠ABE=∠FCE,
∵E为BC中点,∴BE=CE,
在△ABE与△FCE中,,∴△ABE≌△FCE(ASA),∴AB=FC;
(2)∵AD=2AB,AB=FC=CD,∴AD=DF,
∵△ABE≌△FCE,∴AE=EF,∴DE⊥AF.
22.(1)证明:∵四边形ABCD是平行四边形,∴OD=OB,DC∥AB,∴∠FDO=∠EBO,
在△DFO和△BEO中,,∴△DFO≌△BEO(ASA),∴OE=OF.
(2)解:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,OA=OC,
∵EF⊥AC,∴AE=CE,
∵△BEC的周长是10,∴BC+BE+CE=BC+BE+AE=BC+AB=10,
∴ ABCD的周长=2(BC+AB)=20.
23.证明:∵AE⊥AD,CF⊥BC,∴∠EAD=∠FCB=90°,
∵AD∥BC,∴∠ADE=∠CBF,
在Rt△AED和Rt△CFB中,∵,∴Rt△AED≌Rt△CFB(AAS),
∴AD=BC,
∵AD∥BC,∴四边形ABCD是平行四边形.
24.证明:(1)∵Rt△ABC中,∠BAC=30°,∴AB=2BC,
又∵△ABE是等边三角形,EF⊥AB,∴AB=2AF∴AF=BC,
在Rt△AFE和Rt△BCA中,
,∴Rt△AFE≌Rt△BCA(HL),∴AC=EF;
(2)∵△ACD是等边三角形,∴∠DAC=60°,AC=AD,∴∠DAB=∠DAC+∠BAC=90°
又∵EF⊥AB,∴EF∥AD,
∵AC=EF,AC=AD,∴EF=AD,
∴四边形ADFE是平行四边形.
25.证明:(1)∵四边形ABCD是平行四边形,∴AD∥CB,AD=CB,∴∠DAE=∠BCF,
在△ADE和△CBF中,∴△ADE≌△CBF,∴DE=BF.
(2)由(1),可得△ADE≌△CBF,∴∠ADE=∠CBF,
∵∠DEF=∠DAE+∠ADE,∠BFE=∠BCF+∠CBF,∴∠DEF=∠BFE,∴DE∥BF,
又∵DE=BF,
∴四边形DEBF是平行四边形.
26.证明:∵ED∥BC,EF∥AC,∴四边形EFCD是平行四边形,∴DE=CF,
∵BD平分∠ABC,∴∠EBD=∠DBC,
∵DE∥BC,∴∠EDB=∠DBC,∴∠EBD=∠EDB,∴EB=ED,
∴EB=CF.
27.(1)证明:∵AD∥BC,DE∥BF,∴∠E=∠F,∠DAC=∠BCA,∴∠DAE=∠BCF,
在△ADE和△CBF中,,∴△ADE≌△CBF(ASA),∴AD=CB,
∴四边形ABCD是平行四边形;
(2)解:AD=BC、EC=AF、ED=BF、AB=DC;理由如下:
∵△ADE≌△CBF,∴AD=BC,ED=BF,
∵AE=CF,∴EC=AF,∵四边形ABCD是平行四边形,∴AB=DC.
