2.3 变量间的相关关系 课件
文档属性
| 名称 | 2.3 变量间的相关关系 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 755.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-06 10:35:14 | ||
图片预览






文档简介
课件37张PPT。2.3变量之间的相关关系【学 习 目 标】
1、知识与技能:
会画散点图判断线性相关关系,并对实际问题进行分析和预测;加强对线性相关关系及回归直线含义的理解.
2 、过程与方法:
①通过自主探究,体会数形结合、类比的数学思想方法.
②通过动手操作培养学生观察、分析、比较和归纳能力,引出利用计算机等现代化教学工具的必要性.
3、情感、态度与价值观:
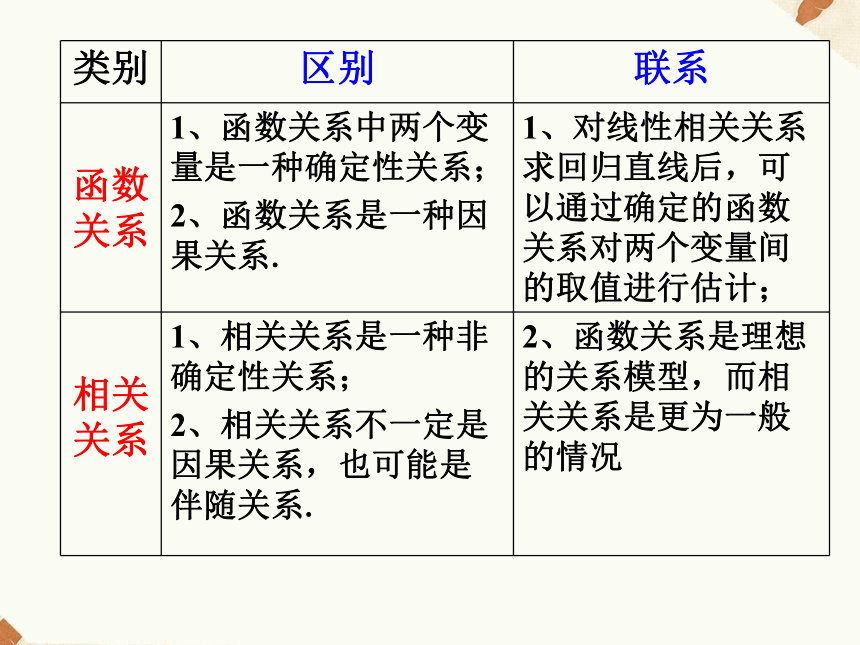
类比函数的表示方法,使学生理解变量间的相关关系,增强对实际问题进行分析和预测的意识.利用计算机让学生动手操作,合作交流激发学生的学习兴趣.创设情境 导入新课 世界遗产——广西巴马长寿村 我国广西省有一个长寿村,名列世界五大长寿地区,村里有个不成文的规矩, “不到八十不祝寿” . 2003年11月,国际自然医学会授予巴马“世界长寿之乡”证书.同学们,知道长寿村长寿的秘密吗?遗传基因、
自然环境、
水、
饮食 问题1、对于两个变量之间的关系,我们之前学过,函数关系是一种确定性关系.那么下列变量与变量之间哪些是确定性的函数关系,哪些是不确定相关关系?①正方形边长与面积之间的关系
②圆的半径与圆的周长之间的关系
③年龄与人体的脂肪含量之间的关系
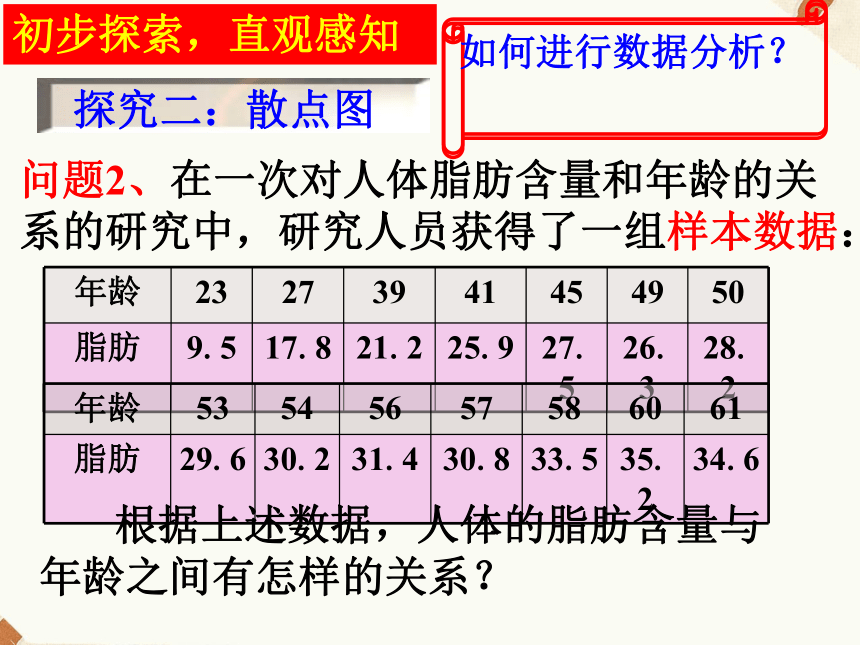
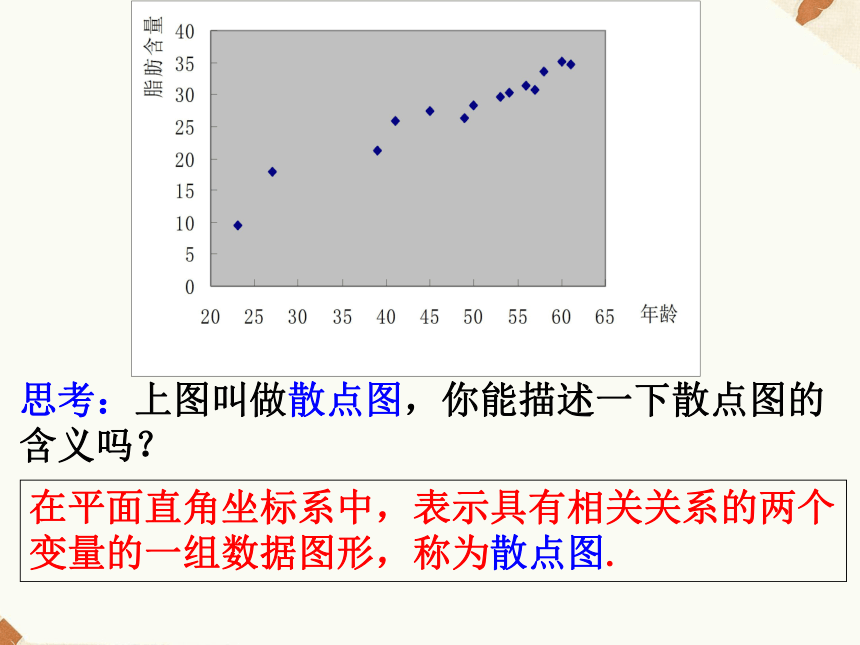
④数学成绩与物理成绩之间的关系.相关关系初步探索,直观感知探究一: 两个变量间的相关关系 请同学们试举几个现实生活中相关关系的例子.问题2、在一次对人体脂肪含量和年龄的关系的研究中,研究人员获得了一组样本数据: 根据上述数据,人体的脂肪含量与年龄之间有怎样的关系?探究二:散点图初步探索,直观感知思考:上图叫做散点图,你能描述一下散点图的含义吗? 在平面直角坐标系中,表示具有相关关系的两个变量的一组数据图形,称为散点图. 种植西红柿,施肥量与产量
之间的散点图 问题3 下面两个散点图中点的分布有什么不同?初步探索,直观感知年龄与脂肪含量之间的散点图 观察左面散点图,发现这些点大致分布在一条直线附 近.
像这样,如果散点图中点的分布从整体上看大致在一条______附近,我们就称这两个变量之间具有线性相 关关系, 这条直线叫做_________.回归直线直线散点图3).如果所有的样本点都落在某一直线附近,
变量之间就有线性相关关系 .1).如果所有的样本点都落在某一函数曲线上,就用该函数来描述变量之间的关系,即变量之间具有函数关系.2).如果所有的样本点都落在某一函数曲线附近,
变量之间就有相关关系.说明散点图:用来判断两个变量是否具有相关关系.
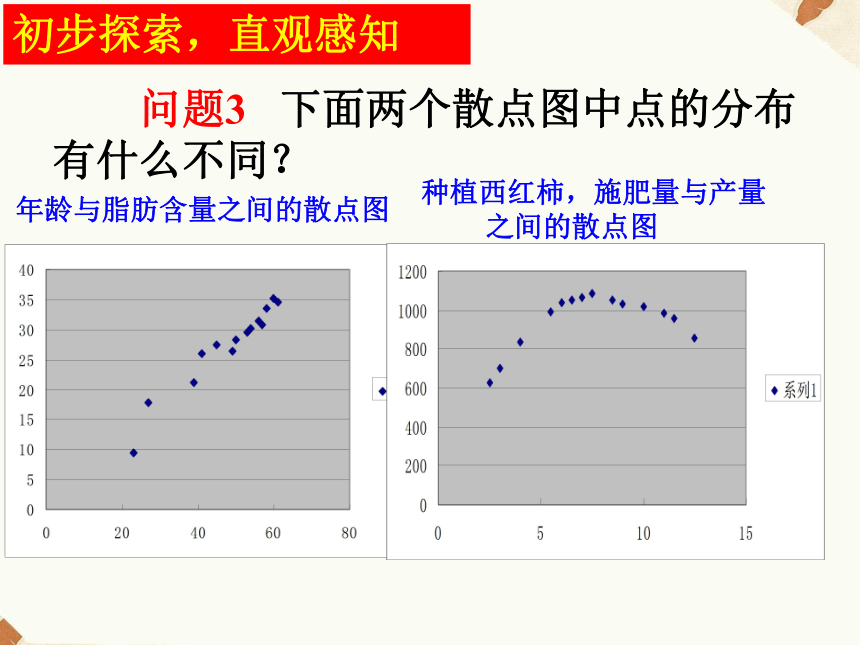
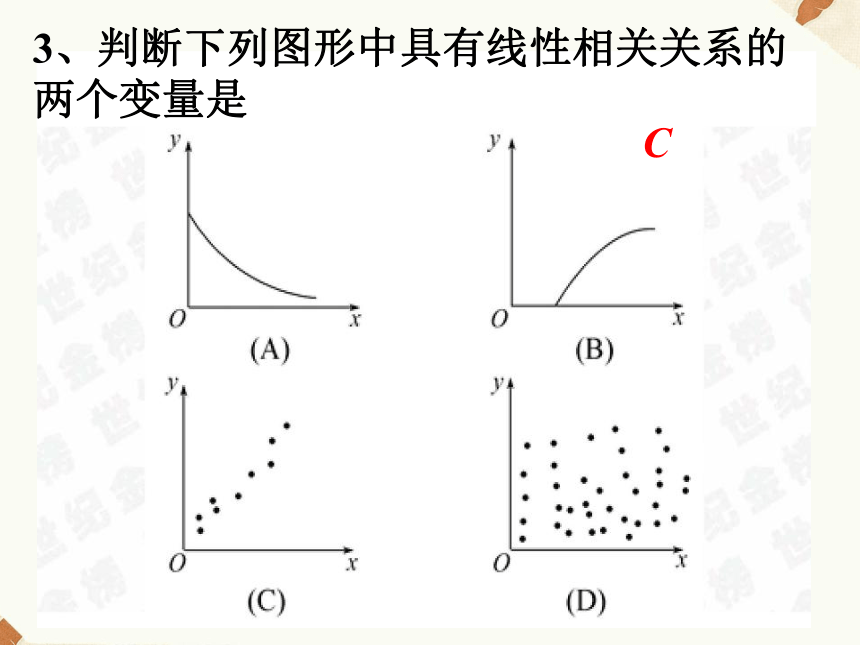
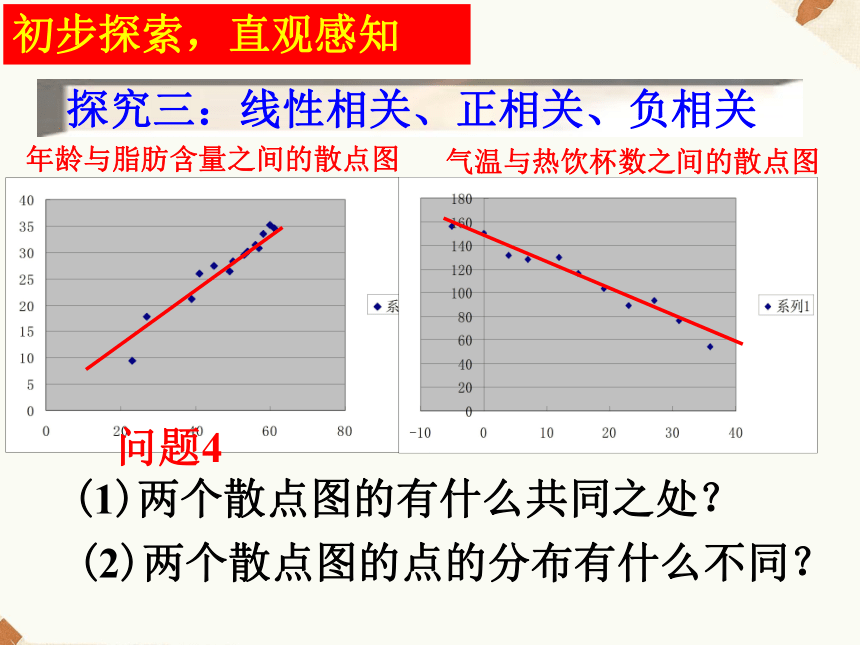
C3、判断下列图形中具有线性相关关系的两个变量是年龄与脂肪含量之间的散点图气温与热饮杯数之间的散点图 问题4
(1)两个散点图的有什么共同之处?探究三:线性相关、正相关、负相关(2)两个散点图的点的分布有什么不同?初步探索,直观感知年龄与脂肪含量之间的散点图气温与热饮杯数之间的散点图探究三:线性相关、正相关、负相关初步探索,直观感知散落在直线的附近线性相关有相同的变化趋势正相关有相反的变化趋势负相关 左面的散点图中,点散布在从左下角到右上角的区域,对于两个变量的这种相关关系,我们将它称为正相关. 右面的散点图中,点散布在从左上角到右下角的区域,对于两个变量的这种相关关系,我们将它称为负相关. 请同学们试举几个现实生活中变量之间成负相关实例. 初步探索,直观感知如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线就叫做回归直线. 这条回归直线的方程,简称为回归方程.回归直线 整体上最接近 方案一:采用测量的方法:先画一条直线,测量出各点到它的距离,然后移动直线,到达一个使距离之和最小的位置,测量出此时直线的斜率和截距,就得到回归方程.如何具体的求出这个回归方程呢?方案二: 在图中选取两点画直线,使得直线两侧的点的个数基本相同.三、如何具体的求出这个回归方程呢?方案三: 在散点图中多取几组点,确定几条直线的方程,分别求出各条直线的斜率和截距的平均数,将这两个平均数作为回归方程的斜率和截距.三、如何具体的求出这个回归方程呢?上述三种方案均有一定的道理,但可靠性不强,我们回到回归直线的定义.求回归方程的关键是如何用数学的方法来刻画“从整体上看,各点与直线的偏差最小”.如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线就叫做回归直线.思考6:对一组具有线性相关关系的样本数据:(x1,y1),(x2,y2),…,(xn,yn),设其回归方程为 可以用哪些数量关系来刻画各样本点与回归直线的接近程度? 当自变量x取xi(i=1,2,…,n)时可以得到回归直
线上的点的纵坐标为:
它与样本数据yi的偏差是: 假设我们已经得到两个具有线性相关关系的样本
的一组数据:(x1,y1),(x2,y2),…,(xn,yn),
且所求回归直线方程是: ,其中 是
待定系数. (x1,y1)(x2,y2)(xn,yn)(x1,y1)(x2,y2)(xn,yn)运算不方便避免相互抵消各点与直线
的整体偏差这种通过求:
的最小值而得到回归直线的方法,即求样本数据的点到
回归直线的距离的平方和最小的方法叫做最小二乘法.4、回归方程的系数公式:回归方程 ,其中: 思考7:利用计算器或计算机可求得年龄和人体脂肪含量的样本数据的回归方程为
,由此我们可以根据一个人个年龄预测其体内脂肪含量的百分比的回归值.若某人65岁,则其体内脂肪含量的百分比约为多少?37.1%
(0.577×65-0.448= 37.1%)若某人65岁,可预测他体内脂肪含量在37.1%(0.577×65-0.448= 37.1%)附近的可能性比较大.
但不能说他体内脂肪含量一定是37.1%
原因:线性回归方程中的截距和斜率都是通过样本估计的,存在随机误差,这种误差可以导致预测结果的偏差,即使截距斜率没有误差,也不可能百分百地保证对应于x,预报值Y能等于实际值y例题:1解:(1)散点图如图示:(2)由题意得:
回归方程为:(3)由回归方程预测,即记忆力为9的同学的判断力约为4.小结1.求样本数据的线性回归方程,可按下列步骤进行:第一步,列表计算平均数 , 第二步,求和 , 第三步,计算 第四步,写出回归方程 变式:(广东高考)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x吨与相应的生产能耗y(吨标准煤)的几组对照数据.(1)请画出上表数据的散点图.
(2)根据上表数据用最小二乘法求出y关于x的线性回归方程
(3)由(2)预测技改后生产100吨甲产品的生产能耗是多少吨标准煤?
(参考数值:2*2.5+3*3+4*4+5*4.5=52.5)解 (1)由题设所给数据,可得散点图如图.(2)对照数据由最小二乘法确定的回归方程的系数为:
=3.5-0.7×3.5=1.05.
因此,所求的线性回归方程为 =0.7x+1.05.(3)当x=100时;所以技改后生产100吨甲产品的生产能耗是71.05吨标准煤(1)散点图:(2)正相关、负相关:(3)线性相关关系:(4)回归方程的系数公式:【知识归纳】1、知识:(1)最小二乘法:(2)转化与化归;
数形结合;2、思想方法:
1、知识与技能:
会画散点图判断线性相关关系,并对实际问题进行分析和预测;加强对线性相关关系及回归直线含义的理解.
2 、过程与方法:
①通过自主探究,体会数形结合、类比的数学思想方法.
②通过动手操作培养学生观察、分析、比较和归纳能力,引出利用计算机等现代化教学工具的必要性.
3、情感、态度与价值观:
类比函数的表示方法,使学生理解变量间的相关关系,增强对实际问题进行分析和预测的意识.利用计算机让学生动手操作,合作交流激发学生的学习兴趣.创设情境 导入新课 世界遗产——广西巴马长寿村 我国广西省有一个长寿村,名列世界五大长寿地区,村里有个不成文的规矩, “不到八十不祝寿” . 2003年11月,国际自然医学会授予巴马“世界长寿之乡”证书.同学们,知道长寿村长寿的秘密吗?遗传基因、
自然环境、
水、
饮食 问题1、对于两个变量之间的关系,我们之前学过,函数关系是一种确定性关系.那么下列变量与变量之间哪些是确定性的函数关系,哪些是不确定相关关系?①正方形边长与面积之间的关系
②圆的半径与圆的周长之间的关系
③年龄与人体的脂肪含量之间的关系
④数学成绩与物理成绩之间的关系.相关关系初步探索,直观感知探究一: 两个变量间的相关关系 请同学们试举几个现实生活中相关关系的例子.问题2、在一次对人体脂肪含量和年龄的关系的研究中,研究人员获得了一组样本数据: 根据上述数据,人体的脂肪含量与年龄之间有怎样的关系?探究二:散点图初步探索,直观感知思考:上图叫做散点图,你能描述一下散点图的含义吗? 在平面直角坐标系中,表示具有相关关系的两个变量的一组数据图形,称为散点图. 种植西红柿,施肥量与产量
之间的散点图 问题3 下面两个散点图中点的分布有什么不同?初步探索,直观感知年龄与脂肪含量之间的散点图 观察左面散点图,发现这些点大致分布在一条直线附 近.
像这样,如果散点图中点的分布从整体上看大致在一条______附近,我们就称这两个变量之间具有线性相 关关系, 这条直线叫做_________.回归直线直线散点图3).如果所有的样本点都落在某一直线附近,
变量之间就有线性相关关系 .1).如果所有的样本点都落在某一函数曲线上,就用该函数来描述变量之间的关系,即变量之间具有函数关系.2).如果所有的样本点都落在某一函数曲线附近,
变量之间就有相关关系.说明散点图:用来判断两个变量是否具有相关关系.
C3、判断下列图形中具有线性相关关系的两个变量是年龄与脂肪含量之间的散点图气温与热饮杯数之间的散点图 问题4
(1)两个散点图的有什么共同之处?探究三:线性相关、正相关、负相关(2)两个散点图的点的分布有什么不同?初步探索,直观感知年龄与脂肪含量之间的散点图气温与热饮杯数之间的散点图探究三:线性相关、正相关、负相关初步探索,直观感知散落在直线的附近线性相关有相同的变化趋势正相关有相反的变化趋势负相关 左面的散点图中,点散布在从左下角到右上角的区域,对于两个变量的这种相关关系,我们将它称为正相关. 右面的散点图中,点散布在从左上角到右下角的区域,对于两个变量的这种相关关系,我们将它称为负相关. 请同学们试举几个现实生活中变量之间成负相关实例. 初步探索,直观感知如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线就叫做回归直线. 这条回归直线的方程,简称为回归方程.回归直线 整体上最接近 方案一:采用测量的方法:先画一条直线,测量出各点到它的距离,然后移动直线,到达一个使距离之和最小的位置,测量出此时直线的斜率和截距,就得到回归方程.如何具体的求出这个回归方程呢?方案二: 在图中选取两点画直线,使得直线两侧的点的个数基本相同.三、如何具体的求出这个回归方程呢?方案三: 在散点图中多取几组点,确定几条直线的方程,分别求出各条直线的斜率和截距的平均数,将这两个平均数作为回归方程的斜率和截距.三、如何具体的求出这个回归方程呢?上述三种方案均有一定的道理,但可靠性不强,我们回到回归直线的定义.求回归方程的关键是如何用数学的方法来刻画“从整体上看,各点与直线的偏差最小”.如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线就叫做回归直线.思考6:对一组具有线性相关关系的样本数据:(x1,y1),(x2,y2),…,(xn,yn),设其回归方程为 可以用哪些数量关系来刻画各样本点与回归直线的接近程度? 当自变量x取xi(i=1,2,…,n)时可以得到回归直
线上的点的纵坐标为:
它与样本数据yi的偏差是: 假设我们已经得到两个具有线性相关关系的样本
的一组数据:(x1,y1),(x2,y2),…,(xn,yn),
且所求回归直线方程是: ,其中 是
待定系数. (x1,y1)(x2,y2)(xn,yn)(x1,y1)(x2,y2)(xn,yn)运算不方便避免相互抵消各点与直线
的整体偏差这种通过求:
的最小值而得到回归直线的方法,即求样本数据的点到
回归直线的距离的平方和最小的方法叫做最小二乘法.4、回归方程的系数公式:回归方程 ,其中: 思考7:利用计算器或计算机可求得年龄和人体脂肪含量的样本数据的回归方程为
,由此我们可以根据一个人个年龄预测其体内脂肪含量的百分比的回归值.若某人65岁,则其体内脂肪含量的百分比约为多少?37.1%
(0.577×65-0.448= 37.1%)若某人65岁,可预测他体内脂肪含量在37.1%(0.577×65-0.448= 37.1%)附近的可能性比较大.
但不能说他体内脂肪含量一定是37.1%
原因:线性回归方程中的截距和斜率都是通过样本估计的,存在随机误差,这种误差可以导致预测结果的偏差,即使截距斜率没有误差,也不可能百分百地保证对应于x,预报值Y能等于实际值y例题:1解:(1)散点图如图示:(2)由题意得:
回归方程为:(3)由回归方程预测,即记忆力为9的同学的判断力约为4.小结1.求样本数据的线性回归方程,可按下列步骤进行:第一步,列表计算平均数 , 第二步,求和 , 第三步,计算 第四步,写出回归方程 变式:(广东高考)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x吨与相应的生产能耗y(吨标准煤)的几组对照数据.(1)请画出上表数据的散点图.
(2)根据上表数据用最小二乘法求出y关于x的线性回归方程
(3)由(2)预测技改后生产100吨甲产品的生产能耗是多少吨标准煤?
(参考数值:2*2.5+3*3+4*4+5*4.5=52.5)解 (1)由题设所给数据,可得散点图如图.(2)对照数据由最小二乘法确定的回归方程的系数为:
=3.5-0.7×3.5=1.05.
因此,所求的线性回归方程为 =0.7x+1.05.(3)当x=100时;所以技改后生产100吨甲产品的生产能耗是71.05吨标准煤(1)散点图:(2)正相关、负相关:(3)线性相关关系:(4)回归方程的系数公式:【知识归纳】1、知识:(1)最小二乘法:(2)转化与化归;
数形结合;2、思想方法:
