2.1.3 分层抽样 课件2
图片预览






文档简介
课件18张PPT。 第二章 统计
2.1.3 分层抽样 简单随机抽样、系统抽样的适用范围和特征是什么?简单随机抽样:①总体容量较小; ②逐个不放回抽取;共性:等可能入样;系统抽样:
①总体容量较大;②编号,分段,定起始号,抽取.
③抓阄法和随机数表法.复习回顾一个著名的案例---泰坦尼克事件 1936年,美国进行总统选举,竞选的是民主党的罗斯福和共和党的兰登,美国权威的《文学摘要》杂志社,为了预测总统候选人谁能当选, 调查者通过电话簿和车辆登记簿上的名单给一大批人发了调查表(注意在1936年电话和汽车只有少数富人拥有).通过分析收回的调查表,显示兰顿非常受欢迎,于是杂志预测兰顿将在选举中获胜.
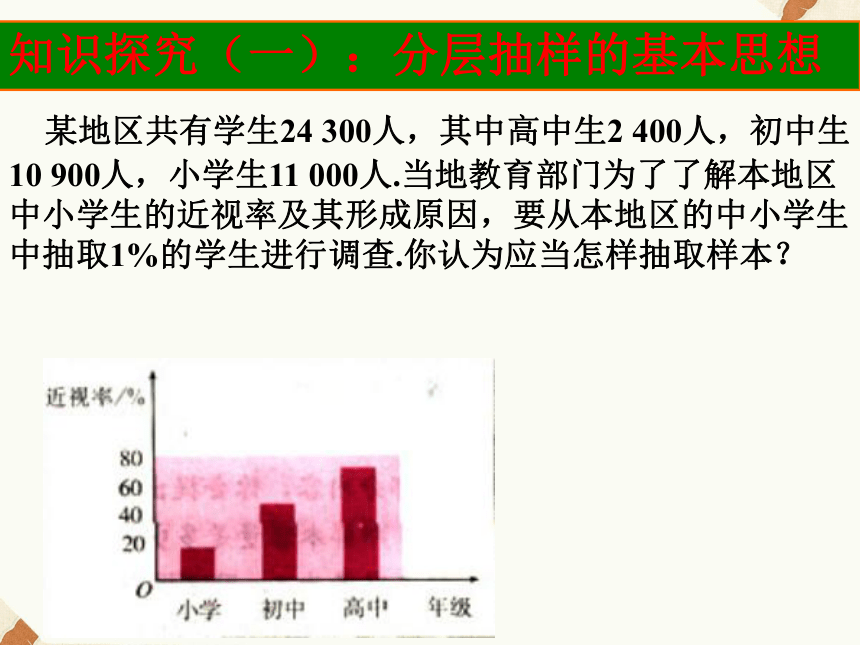
情境引入 实际上选举结果正好相反,最后罗斯福在选举中获胜,其数据如下:情境引入 中国共产党第十八次代表大会2270名代表是从40个单位中产生的,这40个单位分别是:1─31为省(自治区、直辖市)、32中央直属机关、33中央国家机关、34全国台联、35解放军、36武警部队、37中央金融系统、38中央企业系统、39中央香港工委、40中央澳门工委.代表的选举原则上是按各选举单位的党组织数、党员人数进行分配的.知识探究(一):分层抽样的基本思想 某地区共有学生24 300人,其中高中生2 400人,初中生10 900人,小学生11 000人.当地教育部门为了了解本地区中小学生的近视率及其形成原因,要从本地区的中小学生中抽取1%的学生进行调查.你认为应当怎样抽取样本?含有个体多的层,在样本中的代表也应该多,即样本从该层中抽取的个体数也应该多.这样的样本才有更好的代表性.分别利用系统抽样在高中生中抽取
2 400×1%=24人,
在初中生中抽取10 900×1%=109人,
在小学生中抽取11 000×1%=110人.
这种抽样方法称为分层抽样.想一想为什么这样取各个学段的个体数?知识探究(一):分层抽样的基本思想 一般地,在抽样时,将总体分成 的几部分,然后 进行抽样,从各部分抽取一定数量的个体,将各部分取出的个体合在一起作为样本.这种抽样叫做 ,其中所分成的各部分叫 .1.分层抽样定义知识探究(一):分层抽样的基本思想2.分层抽样的适用条件
分层抽样尽量利用事先所掌握的各种信息,并充分考虑保持 与 的一致性,这对提高样本的代表性非常重要.当总体是由 的几个部分组成时,往往选用分层抽样的方法.互不交叉按一定的比例分层抽样“层”样本结构 总体结构 差异明显 总体样本按一定的比例知识探究(一):分层抽样的基本思想说明:①分层抽样时,由于各部分抽取的个体数与这一 部分个体数的比等于样本容量与总体的个体数的比,每一个个体被抽到的可能性都是相等的;
②分层抽样适用于总体由差异明显的几部分组成的情况,在各层抽样时可以根据具体情况采取不同的抽样方法;
③分层抽样中分多少层要是具体情况而定.总的原则是:层内样本的差异要小,而层与层间的差异尽可能地大,否则将失去分层的意义.知识探究(一):分层抽样的基本思想分层抽样的实施步骤:(2) 确定各层应该抽取的个体数.根据总体中 的个体数N与样本容量n确定抽样比(3) 依据抽样比在各层分别按简单随机抽样的方法抽取.确定第i层应该抽取的个体数目 ≈ ×k( 为第i层所包含的个体数),使得各 之和为 .
(4) 综合每层抽样,组成样本.(1) 根据已有信息,将总体分成互不相交的层;注意:对于不能取整的数,求其近似值.知识探究(二):分层抽样的一般步骤然后分别在各年级(层)运用系统抽样方法抽取.解:六年级占 应取 名;
初三年级占 ,应取 名;高三年级占 ,应取 名.
例.某校小学六年级、初中三年级和高中三年级分别有1000,800和700名同学,为了了解全校毕业班学生的视力情况,从以上三个年级中抽取容量为100的样本,你认为应当怎样抽取样本较为合理? 学以致用练习1、 某高中共有900 人,其中高一年级300 人,高二年级200 人,高三年级400 人,现采用分层抽样抽取容量为45的样本,那么高一、高二、高三各年级抽取的人数分别为( )
A.15,5,25 B.15,15,15
C.10,5,30 D.15,10,20D学以致用练习2、某单位有职工160人,其中业务员有104人,管理人员32人,后勤24人,现用分层抽样从中抽取一容量为20的样本,则抽取管理人员( )人
A、3 B、4 C、7 D、12B学以致用练习3、某校共有师生1600人,其中教师100人,现用分层抽样的方法,从所有师生中抽取一个容量为80的样本,则抽取的学生数为 .学以致用练习4、某学校有老师 200人,男学生1200人,女学生1000人,先用分层抽样的方法从全体师生中抽取一个容量为n的样本,已知女学生一共抽取了80人,则n的值为学以致用练习5、已知某校的初中学生人数、高中学生人数、教师人数之比为20:15:2,现在用分层抽样的方法从所有师生中抽取一个容量为N的样本进行调查,若应从高中学生中抽取60人,则N=学以致用简单随
机抽样系统
抽样分层
抽样(1)抽样过程中每个个体被抽取的概率相等
(2)不放回抽样将总体均分成几部分,按预先制定的规则抽取将总体分成几层,按比例分层抽取用简单随机抽样抽取起始号码总体中的个体数较少总体中的个体数较多总体由差异明显的几部分组成从总体中逐个抽取用简单随机抽样或系统抽样对各层抽样探究三 三种抽样方法的比较2.分层抽样是按比例分别对各层进行抽样,再将各个子样本合并在一起构成所需样本.其中正确计算各层应抽取的个体数,是分层抽样过程中的重要环节. 1.分层抽样利用了调查者对调查对象事先掌握的各种信息,考虑了保持样本结构与总体结构的一致性,从而使样本更具有代表性,在实际调查中被广泛应用.3.简单随机抽样是基础,系统抽样与分层抽样是补充和发展,三者相辅相成,对立统一.归纳总结
2.1.3 分层抽样 简单随机抽样、系统抽样的适用范围和特征是什么?简单随机抽样:①总体容量较小; ②逐个不放回抽取;共性:等可能入样;系统抽样:
①总体容量较大;②编号,分段,定起始号,抽取.
③抓阄法和随机数表法.复习回顾一个著名的案例---泰坦尼克事件 1936年,美国进行总统选举,竞选的是民主党的罗斯福和共和党的兰登,美国权威的《文学摘要》杂志社,为了预测总统候选人谁能当选, 调查者通过电话簿和车辆登记簿上的名单给一大批人发了调查表(注意在1936年电话和汽车只有少数富人拥有).通过分析收回的调查表,显示兰顿非常受欢迎,于是杂志预测兰顿将在选举中获胜.
情境引入 实际上选举结果正好相反,最后罗斯福在选举中获胜,其数据如下:情境引入 中国共产党第十八次代表大会2270名代表是从40个单位中产生的,这40个单位分别是:1─31为省(自治区、直辖市)、32中央直属机关、33中央国家机关、34全国台联、35解放军、36武警部队、37中央金融系统、38中央企业系统、39中央香港工委、40中央澳门工委.代表的选举原则上是按各选举单位的党组织数、党员人数进行分配的.知识探究(一):分层抽样的基本思想 某地区共有学生24 300人,其中高中生2 400人,初中生10 900人,小学生11 000人.当地教育部门为了了解本地区中小学生的近视率及其形成原因,要从本地区的中小学生中抽取1%的学生进行调查.你认为应当怎样抽取样本?含有个体多的层,在样本中的代表也应该多,即样本从该层中抽取的个体数也应该多.这样的样本才有更好的代表性.分别利用系统抽样在高中生中抽取
2 400×1%=24人,
在初中生中抽取10 900×1%=109人,
在小学生中抽取11 000×1%=110人.
这种抽样方法称为分层抽样.想一想为什么这样取各个学段的个体数?知识探究(一):分层抽样的基本思想 一般地,在抽样时,将总体分成 的几部分,然后 进行抽样,从各部分抽取一定数量的个体,将各部分取出的个体合在一起作为样本.这种抽样叫做 ,其中所分成的各部分叫 .1.分层抽样定义知识探究(一):分层抽样的基本思想2.分层抽样的适用条件
分层抽样尽量利用事先所掌握的各种信息,并充分考虑保持 与 的一致性,这对提高样本的代表性非常重要.当总体是由 的几个部分组成时,往往选用分层抽样的方法.互不交叉按一定的比例分层抽样“层”样本结构 总体结构 差异明显 总体样本按一定的比例知识探究(一):分层抽样的基本思想说明:①分层抽样时,由于各部分抽取的个体数与这一 部分个体数的比等于样本容量与总体的个体数的比,每一个个体被抽到的可能性都是相等的;
②分层抽样适用于总体由差异明显的几部分组成的情况,在各层抽样时可以根据具体情况采取不同的抽样方法;
③分层抽样中分多少层要是具体情况而定.总的原则是:层内样本的差异要小,而层与层间的差异尽可能地大,否则将失去分层的意义.知识探究(一):分层抽样的基本思想分层抽样的实施步骤:(2) 确定各层应该抽取的个体数.根据总体中 的个体数N与样本容量n确定抽样比(3) 依据抽样比在各层分别按简单随机抽样的方法抽取.确定第i层应该抽取的个体数目 ≈ ×k( 为第i层所包含的个体数),使得各 之和为 .
(4) 综合每层抽样,组成样本.(1) 根据已有信息,将总体分成互不相交的层;注意:对于不能取整的数,求其近似值.知识探究(二):分层抽样的一般步骤然后分别在各年级(层)运用系统抽样方法抽取.解:六年级占 应取 名;
初三年级占 ,应取 名;高三年级占 ,应取 名.
例.某校小学六年级、初中三年级和高中三年级分别有1000,800和700名同学,为了了解全校毕业班学生的视力情况,从以上三个年级中抽取容量为100的样本,你认为应当怎样抽取样本较为合理? 学以致用练习1、 某高中共有900 人,其中高一年级300 人,高二年级200 人,高三年级400 人,现采用分层抽样抽取容量为45的样本,那么高一、高二、高三各年级抽取的人数分别为( )
A.15,5,25 B.15,15,15
C.10,5,30 D.15,10,20D学以致用练习2、某单位有职工160人,其中业务员有104人,管理人员32人,后勤24人,现用分层抽样从中抽取一容量为20的样本,则抽取管理人员( )人
A、3 B、4 C、7 D、12B学以致用练习3、某校共有师生1600人,其中教师100人,现用分层抽样的方法,从所有师生中抽取一个容量为80的样本,则抽取的学生数为 .学以致用练习4、某学校有老师 200人,男学生1200人,女学生1000人,先用分层抽样的方法从全体师生中抽取一个容量为n的样本,已知女学生一共抽取了80人,则n的值为学以致用练习5、已知某校的初中学生人数、高中学生人数、教师人数之比为20:15:2,现在用分层抽样的方法从所有师生中抽取一个容量为N的样本进行调查,若应从高中学生中抽取60人,则N=学以致用简单随
机抽样系统
抽样分层
抽样(1)抽样过程中每个个体被抽取的概率相等
(2)不放回抽样将总体均分成几部分,按预先制定的规则抽取将总体分成几层,按比例分层抽取用简单随机抽样抽取起始号码总体中的个体数较少总体中的个体数较多总体由差异明显的几部分组成从总体中逐个抽取用简单随机抽样或系统抽样对各层抽样探究三 三种抽样方法的比较2.分层抽样是按比例分别对各层进行抽样,再将各个子样本合并在一起构成所需样本.其中正确计算各层应抽取的个体数,是分层抽样过程中的重要环节. 1.分层抽样利用了调查者对调查对象事先掌握的各种信息,考虑了保持样本结构与总体结构的一致性,从而使样本更具有代表性,在实际调查中被广泛应用.3.简单随机抽样是基础,系统抽样与分层抽样是补充和发展,三者相辅相成,对立统一.归纳总结
