2.2.1 用样本的频率分布估计总体分布 课件1
文档属性
| 名称 | 2.2.1 用样本的频率分布估计总体分布 课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 249.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-06 00:00:00 | ||
图片预览






文档简介
课件25张PPT。 第二章 统计
2.2.1 用样本的频率分布估计
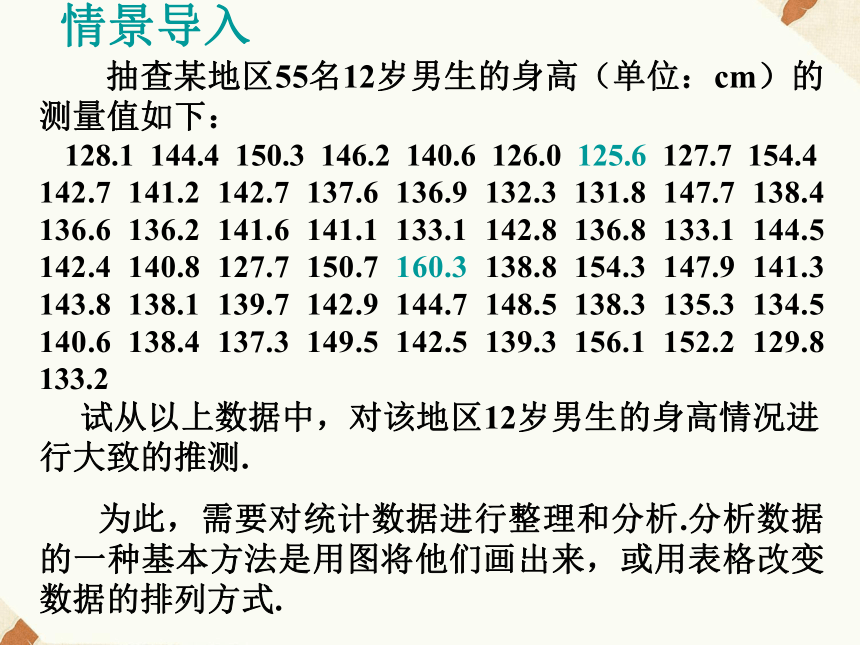
总体分布用样本估计总体 在统计中,用样本的有关情况估计总体的相应情况大体上有两类方法:一、用样本的频率分布去估计总体分布二、用样本的某种数字特征去估计总体相应数字特征 (如平均数、标准差等) 抽查某地区55名12岁男生的身高(单位:cm)的测量值如下:
128.1 144.4 150.3 146.2 140.6 126.0 125.6 127.7 154.4 142.7 141.2 142.7 137.6 136.9 132.3 131.8 147.7 138.4 136.6 136.2 141.6 141.1 133.1 142.8 136.8 133.1 144.5 142.4 140.8 127.7 150.7 160.3 138.8 154.3 147.9 141.3 143.8 138.1 139.7 142.9 144.7 148.5 138.3 135.3 134.5 140.6 138.4 137.3 149.5 142.5 139.3 156.1 152.2 129.8 133.2
试从以上数据中,对该地区12岁男生的身高情况进行大致的推测. 情景导入 为此,需要对统计数据进行整理和分析.分析数据的一种基本方法是用图将他们画出来,或用表格改变数据的排列方式.
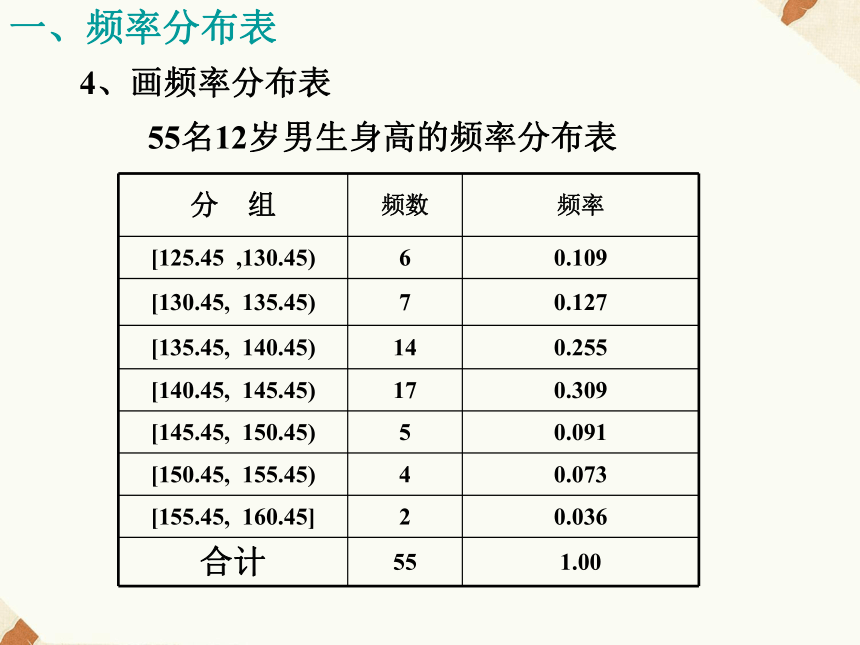
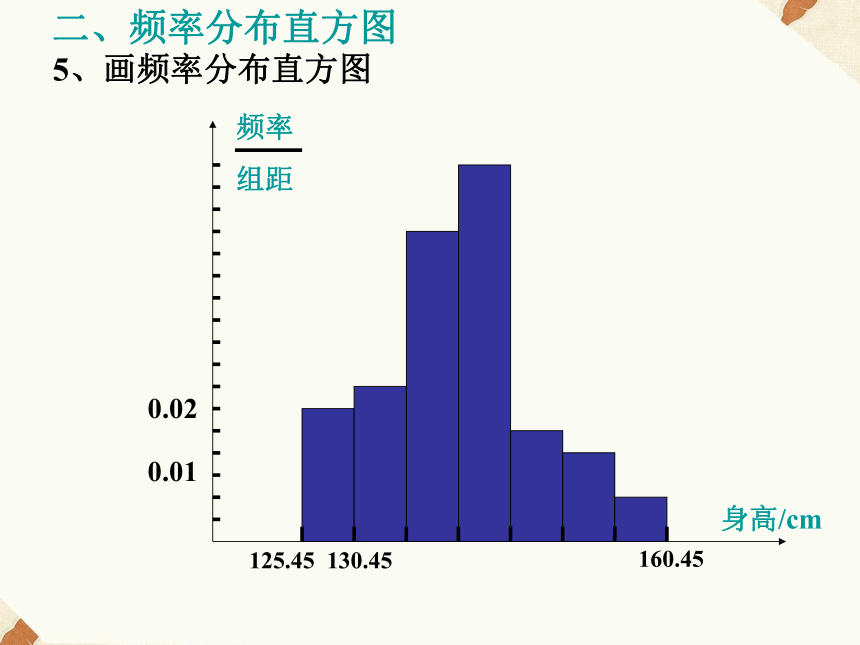
128.1 144.4 150.3 146.2 140.6 126.0 125.6 127.7 154.4 142.7 141.2 142.7 137.6 136.9 132.3 131.8 147.7 138.4 136.6 136.2 141.6 141.1 133.1 142.8 136.8 133.1 144.5 142.4 140.8 127.7 150.7 160.3 138.8 154.3 147.9 141.3 143.8 138.1 139.7 142.9 144.7 148.5 138.3 135.3 134.5 140.6 138.4 137.3 149.5 142.5 139.3 156.1 152.2 129.8 133.2根据以上数据可以画出频数分布表和频数分布图,从图表中可以清楚地知道数据分布在各个小组的个数.频率分布表和频率分布图,则从各个小组的数据在样本容量中所占比例的大小来表示数据分布的规律.画频率分布直方图的具体做法如下:1、求极差(最大值与最小值的差)160.3-125.6=34.72、决定组距与组数(将数据分组)组数=极差/组距=34.7/5≈6.9因此组距为5,组数为73、将数据分组4、画频率分布表[125.45 ,130.45), [130.45, 135.45) ,[135.45, 140.45), [140.45, 145.45), [145.45, 150.45), [150.45,155.45) ,[155.45, 160.45]55名12岁男生身高的频率分布表一、频率分布表4、画频率分布表5、画频率分布直方图二、频率分布直方图1、频率分布表列出的是数据落在各个小组的频率.2、频率分布直方图是用面积表示数据落在各个小组的频率的大小.在频率分布直方图中,各小长方形面积之和为1.说明:画频率分布直方图的一般步骤:1、求极差(最大值与最小值的差)2、决定组距与组数(将数据分组)组数=极差/组距当样本容量不超过100时,组数一般为5~12组5、画频率分布直方图4、画频率分布表二、频率分布直方图3、将数据分组三、频率分布折线图随着样本容量的增加,作图时所分的组数增加,组距减小,相应的频率折线图会越来越接近于一条光滑曲线,统计中称这条光滑曲线为总体密度曲线.四、总体密度曲线四、总体密度曲线身高ab (图中阴影部分的面积,表示总体在区间 (a, b) 内取值的百分比).反映了总体分布,即反映了总体在各个范围内取值的百分比说明:总体密度曲线是客观存在的,但在实际中,我们只能用样本来估计.由于样本是随机的,不同的样本得到的频率分布折线图不同;即使是同一样本,不同的分组得到的频率分布折线图也不同.也就是说:频率分布折线图是随着样本的容量和分组情况的变化而变化的,因此不能由样本的频率分布折线图得到准确的总体密度曲线.例1、为了了解某地高一年级男生的身高情况,从其中的一个学校选取容量为60的样本(60名男生的身高,单位:cm),分组情况如下:60.4527例2、一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图,为了分析居民的收入与年龄、学历、职业等方面的联系,要从这10000人中再用分层抽样的方法抽出100人作进一步调查,则在[2500,3000](元)月收入段应抽出 人25试验1、进行“抛掷硬币”试验的试验结果画出频率分布的条形图 注意点:①各直方长条的宽度要相同;②相邻长条之间的间隔要适当结论:当试验次数无限增大时,01两种试验结果的频率大致相同.五、总体分布 排除了抽样造成的误差,精确地反映了总体取值的概率分布规律.这种总体取值的概率分布规律通常成为总体分布. (2)研究总体概率分布往往可以研究其频数分布、频率分布.频率分布与总体分布的关系: (1)通过样本的频数分布、频率分布可以估计总体的概率分布. 抽样过程中加大样本容量, 排除抽样造成的误差,这样样本的分布频率精确地反映了总体取值的概率分布规律.用样本的频率分布估计总体分布,可以分为两种情况.
(1)当总体中的个体取不同数值很少时,如试验1,其几何表示用条形图;
(2) 当总体中的个体取不同数值较多、甚至无限时或总体可以在一个实数区间内取值,如试验2,其几何表示用直方图.说明:以上两种情况的不同之处在于:前者的频率分布表列出的是几个不同数值的频率,条形图用其高度来表示取各个值的频率;后者的频率分布表列出的是在各个不同区间内取值的频率,直方图用其图形面积的大小来表示在各个区间内取值的频率,各长方形面积之和为1.NBA某赛季甲、乙两名篮球运动员每场比赛的得分 的原始纪录如下: 甲运动员得分:13,51,23,8,26,38,16,33,14,28,39; 乙运动员得分:49,24,12,31,50,31,44,36,15,37,25,36,39. 问题一:请用适当的方法表示上述数据,并对两名运动员的得分能力进行比较.六、茎叶图 问题二:用上次课所学的制作样本的频率分布直方图来分析好吗? 甲:13,51,23,8,26,38,16,33,14,28,39; 乙:49,24,12,31,50,31,44,36,15,37,25,36,39.当数据比较少时,应用列分布直方图反而不方便 简化制图格式和步骤,得到新的统计制图方法:甲运动员得分:13,51,23,8,26,38,16,
33,14,28,39; 乙运动员得分:49,24,12,31,50,31,44,
36,15,37,25,36,39.茎叶图茎叶图:顾名思义,茎是指中间的一列数,叶 就是从茎的旁边生长出来的数.中间的数字表示 得分的十位数,旁边的数字分别表示两个人得分 的个位数.茎叶图特点:茎叶图不仅能保留原始数据,而且能够展示数据
的分布情况 .乙:得分基本上是对称的,叶的分布是“单峰”的,有10/13的叶是分布在茎2、3、4上,中位数是36.
甲:得分除一个特殊得分(51分)外,也大致对称,分布也是“单峰”的,有9/11的叶主要集中在茎1、2、3上,中位数是26. 从上述中位数的大小就可以看得出,乙运动员的成绩更好.另外,乙运动员的得分更集中于峰值附近,这说明乙运动员的发挥更稳定.
2.2.1 用样本的频率分布估计
总体分布用样本估计总体 在统计中,用样本的有关情况估计总体的相应情况大体上有两类方法:一、用样本的频率分布去估计总体分布二、用样本的某种数字特征去估计总体相应数字特征 (如平均数、标准差等) 抽查某地区55名12岁男生的身高(单位:cm)的测量值如下:
128.1 144.4 150.3 146.2 140.6 126.0 125.6 127.7 154.4 142.7 141.2 142.7 137.6 136.9 132.3 131.8 147.7 138.4 136.6 136.2 141.6 141.1 133.1 142.8 136.8 133.1 144.5 142.4 140.8 127.7 150.7 160.3 138.8 154.3 147.9 141.3 143.8 138.1 139.7 142.9 144.7 148.5 138.3 135.3 134.5 140.6 138.4 137.3 149.5 142.5 139.3 156.1 152.2 129.8 133.2
试从以上数据中,对该地区12岁男生的身高情况进行大致的推测. 情景导入 为此,需要对统计数据进行整理和分析.分析数据的一种基本方法是用图将他们画出来,或用表格改变数据的排列方式.
128.1 144.4 150.3 146.2 140.6 126.0 125.6 127.7 154.4 142.7 141.2 142.7 137.6 136.9 132.3 131.8 147.7 138.4 136.6 136.2 141.6 141.1 133.1 142.8 136.8 133.1 144.5 142.4 140.8 127.7 150.7 160.3 138.8 154.3 147.9 141.3 143.8 138.1 139.7 142.9 144.7 148.5 138.3 135.3 134.5 140.6 138.4 137.3 149.5 142.5 139.3 156.1 152.2 129.8 133.2根据以上数据可以画出频数分布表和频数分布图,从图表中可以清楚地知道数据分布在各个小组的个数.频率分布表和频率分布图,则从各个小组的数据在样本容量中所占比例的大小来表示数据分布的规律.画频率分布直方图的具体做法如下:1、求极差(最大值与最小值的差)160.3-125.6=34.72、决定组距与组数(将数据分组)组数=极差/组距=34.7/5≈6.9因此组距为5,组数为73、将数据分组4、画频率分布表[125.45 ,130.45), [130.45, 135.45) ,[135.45, 140.45), [140.45, 145.45), [145.45, 150.45), [150.45,155.45) ,[155.45, 160.45]55名12岁男生身高的频率分布表一、频率分布表4、画频率分布表5、画频率分布直方图二、频率分布直方图1、频率分布表列出的是数据落在各个小组的频率.2、频率分布直方图是用面积表示数据落在各个小组的频率的大小.在频率分布直方图中,各小长方形面积之和为1.说明:画频率分布直方图的一般步骤:1、求极差(最大值与最小值的差)2、决定组距与组数(将数据分组)组数=极差/组距当样本容量不超过100时,组数一般为5~12组5、画频率分布直方图4、画频率分布表二、频率分布直方图3、将数据分组三、频率分布折线图随着样本容量的增加,作图时所分的组数增加,组距减小,相应的频率折线图会越来越接近于一条光滑曲线,统计中称这条光滑曲线为总体密度曲线.四、总体密度曲线四、总体密度曲线身高ab (图中阴影部分的面积,表示总体在区间 (a, b) 内取值的百分比).反映了总体分布,即反映了总体在各个范围内取值的百分比说明:总体密度曲线是客观存在的,但在实际中,我们只能用样本来估计.由于样本是随机的,不同的样本得到的频率分布折线图不同;即使是同一样本,不同的分组得到的频率分布折线图也不同.也就是说:频率分布折线图是随着样本的容量和分组情况的变化而变化的,因此不能由样本的频率分布折线图得到准确的总体密度曲线.例1、为了了解某地高一年级男生的身高情况,从其中的一个学校选取容量为60的样本(60名男生的身高,单位:cm),分组情况如下:60.4527例2、一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图,为了分析居民的收入与年龄、学历、职业等方面的联系,要从这10000人中再用分层抽样的方法抽出100人作进一步调查,则在[2500,3000](元)月收入段应抽出 人25试验1、进行“抛掷硬币”试验的试验结果画出频率分布的条形图 注意点:①各直方长条的宽度要相同;②相邻长条之间的间隔要适当结论:当试验次数无限增大时,01两种试验结果的频率大致相同.五、总体分布 排除了抽样造成的误差,精确地反映了总体取值的概率分布规律.这种总体取值的概率分布规律通常成为总体分布. (2)研究总体概率分布往往可以研究其频数分布、频率分布.频率分布与总体分布的关系: (1)通过样本的频数分布、频率分布可以估计总体的概率分布. 抽样过程中加大样本容量, 排除抽样造成的误差,这样样本的分布频率精确地反映了总体取值的概率分布规律.用样本的频率分布估计总体分布,可以分为两种情况.
(1)当总体中的个体取不同数值很少时,如试验1,其几何表示用条形图;
(2) 当总体中的个体取不同数值较多、甚至无限时或总体可以在一个实数区间内取值,如试验2,其几何表示用直方图.说明:以上两种情况的不同之处在于:前者的频率分布表列出的是几个不同数值的频率,条形图用其高度来表示取各个值的频率;后者的频率分布表列出的是在各个不同区间内取值的频率,直方图用其图形面积的大小来表示在各个区间内取值的频率,各长方形面积之和为1.NBA某赛季甲、乙两名篮球运动员每场比赛的得分 的原始纪录如下: 甲运动员得分:13,51,23,8,26,38,16,33,14,28,39; 乙运动员得分:49,24,12,31,50,31,44,36,15,37,25,36,39. 问题一:请用适当的方法表示上述数据,并对两名运动员的得分能力进行比较.六、茎叶图 问题二:用上次课所学的制作样本的频率分布直方图来分析好吗? 甲:13,51,23,8,26,38,16,33,14,28,39; 乙:49,24,12,31,50,31,44,36,15,37,25,36,39.当数据比较少时,应用列分布直方图反而不方便 简化制图格式和步骤,得到新的统计制图方法:甲运动员得分:13,51,23,8,26,38,16,
33,14,28,39; 乙运动员得分:49,24,12,31,50,31,44,
36,15,37,25,36,39.茎叶图茎叶图:顾名思义,茎是指中间的一列数,叶 就是从茎的旁边生长出来的数.中间的数字表示 得分的十位数,旁边的数字分别表示两个人得分 的个位数.茎叶图特点:茎叶图不仅能保留原始数据,而且能够展示数据
的分布情况 .乙:得分基本上是对称的,叶的分布是“单峰”的,有10/13的叶是分布在茎2、3、4上,中位数是36.
甲:得分除一个特殊得分(51分)外,也大致对称,分布也是“单峰”的,有9/11的叶主要集中在茎1、2、3上,中位数是26. 从上述中位数的大小就可以看得出,乙运动员的成绩更好.另外,乙运动员的得分更集中于峰值附近,这说明乙运动员的发挥更稳定.
