2.2.1 用样本的频率分布估计总体分布 同步练习4(含答案)
文档属性
| 名称 | 2.2.1 用样本的频率分布估计总体分布 同步练习4(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 254.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-06 11:04:09 | ||
图片预览



文档简介
2.2.1
用样本的频率分布估计总体分布
同步练习
1.在抽查某产品尺寸的过程中,将其尺寸分成若干组,[a,b)是其中一组,抽查出的个体数在该组内的频率为m,该组直方图的高为h,则|a-b|的值等于( )
A.h·m
B.
C.
D.与m,h无关
解析:选B.小长方形的高=,
∴|a-b|==.
某雷达测速区规定:凡车速大于或等于70
km/h的汽车视为“超速”,并将受到处罚,如图是某路段的一个检测点对300辆汽车的车速进行检测所得结果的频率分布直方图,则从图中可得出将被处罚的汽车数为( )
A.30辆
B.40辆
C.60辆
D.80辆
解析:选C.车速大于或等于70
km/h的汽车数为0.02×10×300=60(辆).故选C.
某超市连锁店统计了城市甲、乙的各16台自动售货机在12∶00至13∶00间的销售金额,并用茎叶图表示如图.则有( )
A.甲城市销售额多,乙城市销售额不够稳定
B.甲城市销售额多,乙城市销售额稳定
C.乙城市销售额多,甲城市销售额稳定
D.乙城市销售额多,甲城市销售额不够稳定
解析:选D.十位数字是3、4、5时乙城市的销售额明显多于甲,估计乙城市销售额多,甲的数字过于分散,不够稳定.故选D.
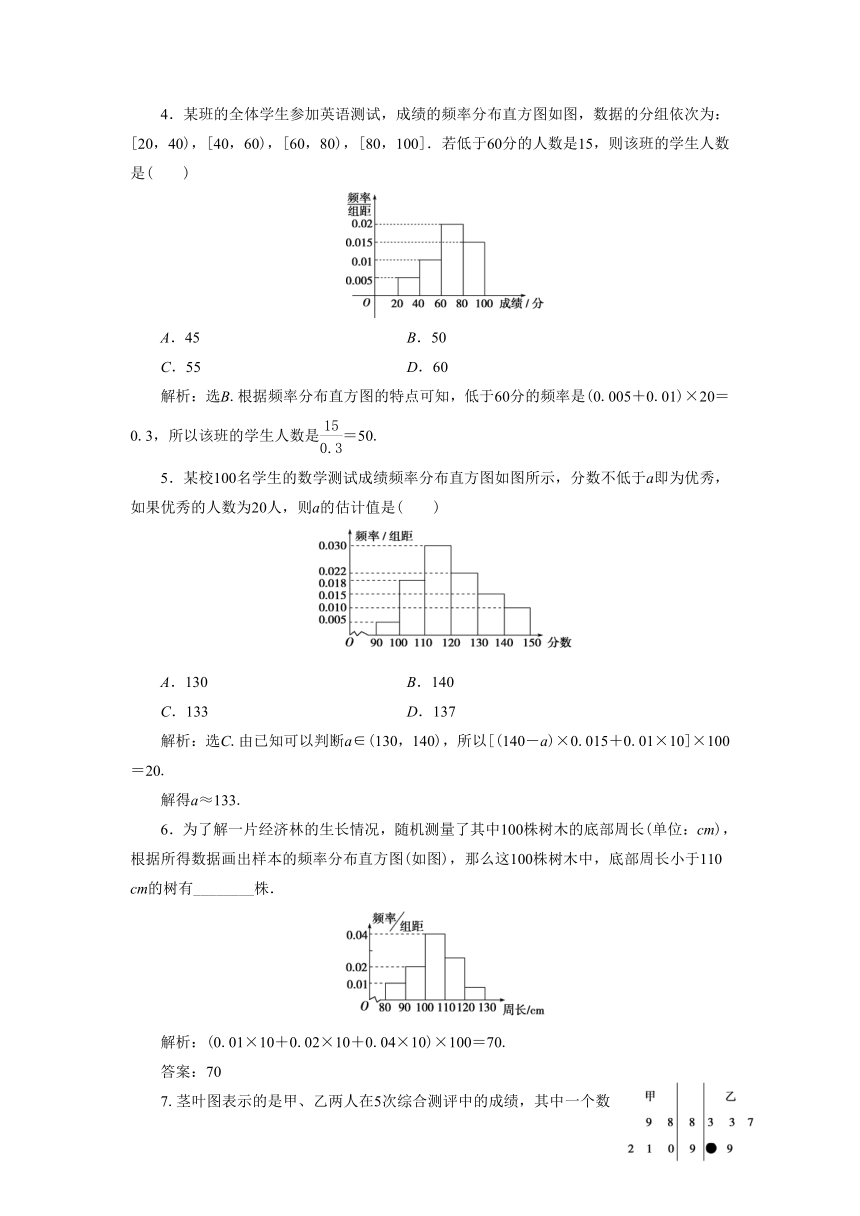
4.某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100].若低于60分的人数是15,则该班的学生人数是( )
A.45
B.50
C.55
D.60
解析:选B.根据频率分布直方图的特点可知,低于60分的频率是(0.005+0.01)×20=0.3,所以该班的学生人数是=50.
5.某校100名学生的数学测试成绩频率分布直方图如图所示,分数不低于a即为优秀,如果优秀的人数为20人,则a的估计值是( )
A.130
B.140
C.133
D.137
解析:选C.由已知可以判断a∈(130,140),所以[(140-a)×0.015+0.01×10]×100=20.
解得a≈133.
6.为了解一片经济林的生长情况,随机测量了其中100株树木的底部周长(单位:cm),根据所得数据画出样本的频率分布直方图(如图),那么这100株树木中,底部周长小于110
cm的树有________株.
解析:(0.01×10+0.02×10+0.04×10)×100=70.
答案:70
7.茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,若乙的平均分是89,则污损的数字是________.
解析:设污损的叶对应的成绩是x,由茎叶图可得89×5=83+83+87+x+99,所以x=93,故污损的数字是3.
答案:3
8.为了帮助班上的两名贫困生解决经济困难,班上的20名同学捐出了自己的零花钱,他们捐款数(单位:元)如下:19,20,25,30,24,23,25,29,27,27,28,28,26,27,21,30,20,19,22,20.班主任老师准备将这组数据制成频率分布直方图,以表彰他们的爱心.制图时先计算最大值与最小值的差是________.若取组距为2,则应分成________组;若第一组的起点定为18.5,则在[26.5,28.5)内的频数为________.
解析:由题意知,极差为30-19=11;由于组距为2,则=5.5不是整数,所以取6组;捐款数落在[26.5,28.5)内的有27,27,28,28,27共5个,因此频数为5.
答案:11 6 5
9.某中学高二(2)班甲、乙两名学生自进入高中以来,每次数学考试成绩情况如下:
甲:95,81,75,91,86,89,71,65,76,88,94,110,107;
乙:83,86,93,99,88,103,98,114,98,79,78,106,101.
画出两人数学成绩的茎叶图,并根据茎叶图对两人的成绩进行比较.
解:甲、乙两人数学成绩的茎叶图如图所示.
从这个茎叶图上可以看出,乙同学的得分情况是大致对称的,中位数是98;甲同学的得分情况也大致对称,中位数是88.乙同学的成绩比较稳定,总体情况比甲同学好.
10.为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
(1)填充频率分布表的空格(将答案直接填在表格内);
分组
频数
频率
[50,60)
4
0.08
[60,70)
0.16
[70,80)
10
[80,90)
16
0.32
[90,100]
合计
50
(2)补全频率分布直方图
(3)若成绩在[70,90)分的学生为二等奖,问获得二等奖的学生约为多少人?
解:(1)
分组
频数
频率
[50,60)
4
0.08]
[60,70)
8
0.16
[70,80)
10
0.20
[80,90)
16
0.32
[90,100]
12
0.24
合计
50
1.00
(2)频率分布直方图如图所示:
(3)∵成绩在[70,80)间的学生频率为0.20;
成绩在[80,90)间的学生频率为0.32,
∴在[70,90)之间的频率为0.20+0.32=0.52.
又∵900名学生参加竞赛,
∴该校获二等奖的学生为900×0.52=468(人).
[高考水平训练]
1.
某学校随机抽取20个班,调查各班中有网上购物经历的人数,所得数据的茎叶图如图所示.以组距为5将数据分组成[0,5),[5,10),…,[30,35),[35,40]时,所作的频率分布直方图是( )
解析:选A.法一:由题意知样本容量为20,组距为5.
列表如下:
分组
频数
频率
[0,5)
1
0.01
[5,10)
1
0.01
[10,15)
4
0.04
[15,20)
2
0.02
[20,25)
4
0.04
[25,30)
3
0.03
[30,35)
3
0.03
[35,40]
2
0.02
合计
20
1
观察各选择项的频率分布直方图知选A.
法二:由茎叶图知落在区间[0,5)与[5,10)上的频数相等,故频率、也分别相等.比较四个选项知A正确,故选A.
2.从甲、乙两个品种的棉花中各抽测了25根棉花的纤维长度(单位:mm),结果如下:
甲品种:271 273 280 285 285 287 292 294 295 301 303 303 307 308 310 314 319 323
325 325 328 331 334 337 352
乙品种:284 292 295 304 306 307 312 313 315 315 316 318 318 320 322 322 324 327
329 331 333 336 337 343 356
由以上数据设计的茎叶图如图所示:
根据以上茎叶图,对甲、乙两个品种棉花的纤维长度作比较,写出两个统计结论:
①________________________________________________________________________
________________________________________________________________________;
②_______________________________________________________________________
________________________________________________________________________.
解析:由茎叶图可以看出甲品种棉花的纤维长度比较分散,乙品种棉花的纤维长度比较集中(大部分集中在312~337之间)等,通过分析可以得到答案.
答案:①从茎叶图上看,甲品种棉花的纤维长度较分散,而乙品种棉花的纤维长度比较集中
②甲品种棉花的纤维长度中位数是303,乙品种棉花的纤维长度中位数是318,并且它们的对称性较好,因此乙品种的平均长度大于甲品种的平均长度
3.近年来,我国“雾霾天气”频发,严重影响人们的身体健康.根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:
API
0~50
51~100
101~150
151~200
201~250
251~300
>300
级别
Ⅰ
Ⅱ
Ⅲ1
Ⅲ2
Ⅳ1
Ⅳ2
Ⅴ
状况
优
良
轻微污染
轻度污染
中度污染
中度重污染
重度污染
对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间[0,50],(50,100],(100,150],(150,200],(200,250],(250,300]进行分组,得到频率分布直方图如图.
(1)求频率分布直方图中x的值;
(2)计算一年中空气质量分别为良和轻微污染的天数.
解:(1)根据频率分布直方图可知,
x=÷50=.
(2)空气质量为Y的天数=(Y对应的频率÷组距)×组距×365天,所以一年中空气质量为良和轻微污染的天数分别是×50×365=119(天)和×50×365=100(天).
4.某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),下面是这次调查统计分析得到的频率分布表和频率分布直方图(如图所示).
分组
频数
频率
一组
0≤t<5
0
0
二组
5≤t<10
10
0.10
三组
10≤t<15
10
②
四组
15≤t<20
①
0.50
五组
20≤t≤25
30
0.30
合计
100
1.00
解答下列问题:
(1)这次抽样的样本容量是多少?
(2)在表中填写出缺失的数据并补全频率分布直方图;
(3)旅客购票用时的平均数可能落在哪一组?
解:(1)样本容量是100.
(2)①50 ②0.10
所补频率分布直方图如图中的阴影部分:
(3)设旅客平均购票用时为t
min,则有
≤t<
,
即15≤t<20.
所以旅客购票用时的平均数可能落在第四组.
用样本的频率分布估计总体分布
同步练习
1.在抽查某产品尺寸的过程中,将其尺寸分成若干组,[a,b)是其中一组,抽查出的个体数在该组内的频率为m,该组直方图的高为h,则|a-b|的值等于( )
A.h·m
B.
C.
D.与m,h无关
解析:选B.小长方形的高=,
∴|a-b|==.
某雷达测速区规定:凡车速大于或等于70
km/h的汽车视为“超速”,并将受到处罚,如图是某路段的一个检测点对300辆汽车的车速进行检测所得结果的频率分布直方图,则从图中可得出将被处罚的汽车数为( )
A.30辆
B.40辆
C.60辆
D.80辆
解析:选C.车速大于或等于70
km/h的汽车数为0.02×10×300=60(辆).故选C.
某超市连锁店统计了城市甲、乙的各16台自动售货机在12∶00至13∶00间的销售金额,并用茎叶图表示如图.则有( )
A.甲城市销售额多,乙城市销售额不够稳定
B.甲城市销售额多,乙城市销售额稳定
C.乙城市销售额多,甲城市销售额稳定
D.乙城市销售额多,甲城市销售额不够稳定
解析:选D.十位数字是3、4、5时乙城市的销售额明显多于甲,估计乙城市销售额多,甲的数字过于分散,不够稳定.故选D.
4.某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100].若低于60分的人数是15,则该班的学生人数是( )
A.45
B.50
C.55
D.60
解析:选B.根据频率分布直方图的特点可知,低于60分的频率是(0.005+0.01)×20=0.3,所以该班的学生人数是=50.
5.某校100名学生的数学测试成绩频率分布直方图如图所示,分数不低于a即为优秀,如果优秀的人数为20人,则a的估计值是( )
A.130
B.140
C.133
D.137
解析:选C.由已知可以判断a∈(130,140),所以[(140-a)×0.015+0.01×10]×100=20.
解得a≈133.
6.为了解一片经济林的生长情况,随机测量了其中100株树木的底部周长(单位:cm),根据所得数据画出样本的频率分布直方图(如图),那么这100株树木中,底部周长小于110
cm的树有________株.
解析:(0.01×10+0.02×10+0.04×10)×100=70.
答案:70
7.茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,若乙的平均分是89,则污损的数字是________.
解析:设污损的叶对应的成绩是x,由茎叶图可得89×5=83+83+87+x+99,所以x=93,故污损的数字是3.
答案:3
8.为了帮助班上的两名贫困生解决经济困难,班上的20名同学捐出了自己的零花钱,他们捐款数(单位:元)如下:19,20,25,30,24,23,25,29,27,27,28,28,26,27,21,30,20,19,22,20.班主任老师准备将这组数据制成频率分布直方图,以表彰他们的爱心.制图时先计算最大值与最小值的差是________.若取组距为2,则应分成________组;若第一组的起点定为18.5,则在[26.5,28.5)内的频数为________.
解析:由题意知,极差为30-19=11;由于组距为2,则=5.5不是整数,所以取6组;捐款数落在[26.5,28.5)内的有27,27,28,28,27共5个,因此频数为5.
答案:11 6 5
9.某中学高二(2)班甲、乙两名学生自进入高中以来,每次数学考试成绩情况如下:
甲:95,81,75,91,86,89,71,65,76,88,94,110,107;
乙:83,86,93,99,88,103,98,114,98,79,78,106,101.
画出两人数学成绩的茎叶图,并根据茎叶图对两人的成绩进行比较.
解:甲、乙两人数学成绩的茎叶图如图所示.
从这个茎叶图上可以看出,乙同学的得分情况是大致对称的,中位数是98;甲同学的得分情况也大致对称,中位数是88.乙同学的成绩比较稳定,总体情况比甲同学好.
10.为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
(1)填充频率分布表的空格(将答案直接填在表格内);
分组
频数
频率
[50,60)
4
0.08
[60,70)
0.16
[70,80)
10
[80,90)
16
0.32
[90,100]
合计
50
(2)补全频率分布直方图
(3)若成绩在[70,90)分的学生为二等奖,问获得二等奖的学生约为多少人?
解:(1)
分组
频数
频率
[50,60)
4
0.08]
[60,70)
8
0.16
[70,80)
10
0.20
[80,90)
16
0.32
[90,100]
12
0.24
合计
50
1.00
(2)频率分布直方图如图所示:
(3)∵成绩在[70,80)间的学生频率为0.20;
成绩在[80,90)间的学生频率为0.32,
∴在[70,90)之间的频率为0.20+0.32=0.52.
又∵900名学生参加竞赛,
∴该校获二等奖的学生为900×0.52=468(人).
[高考水平训练]
1.
某学校随机抽取20个班,调查各班中有网上购物经历的人数,所得数据的茎叶图如图所示.以组距为5将数据分组成[0,5),[5,10),…,[30,35),[35,40]时,所作的频率分布直方图是( )
解析:选A.法一:由题意知样本容量为20,组距为5.
列表如下:
分组
频数
频率
[0,5)
1
0.01
[5,10)
1
0.01
[10,15)
4
0.04
[15,20)
2
0.02
[20,25)
4
0.04
[25,30)
3
0.03
[30,35)
3
0.03
[35,40]
2
0.02
合计
20
1
观察各选择项的频率分布直方图知选A.
法二:由茎叶图知落在区间[0,5)与[5,10)上的频数相等,故频率、也分别相等.比较四个选项知A正确,故选A.
2.从甲、乙两个品种的棉花中各抽测了25根棉花的纤维长度(单位:mm),结果如下:
甲品种:271 273 280 285 285 287 292 294 295 301 303 303 307 308 310 314 319 323
325 325 328 331 334 337 352
乙品种:284 292 295 304 306 307 312 313 315 315 316 318 318 320 322 322 324 327
329 331 333 336 337 343 356
由以上数据设计的茎叶图如图所示:
根据以上茎叶图,对甲、乙两个品种棉花的纤维长度作比较,写出两个统计结论:
①________________________________________________________________________
________________________________________________________________________;
②_______________________________________________________________________
________________________________________________________________________.
解析:由茎叶图可以看出甲品种棉花的纤维长度比较分散,乙品种棉花的纤维长度比较集中(大部分集中在312~337之间)等,通过分析可以得到答案.
答案:①从茎叶图上看,甲品种棉花的纤维长度较分散,而乙品种棉花的纤维长度比较集中
②甲品种棉花的纤维长度中位数是303,乙品种棉花的纤维长度中位数是318,并且它们的对称性较好,因此乙品种的平均长度大于甲品种的平均长度
3.近年来,我国“雾霾天气”频发,严重影响人们的身体健康.根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:
API
0~50
51~100
101~150
151~200
201~250
251~300
>300
级别
Ⅰ
Ⅱ
Ⅲ1
Ⅲ2
Ⅳ1
Ⅳ2
Ⅴ
状况
优
良
轻微污染
轻度污染
中度污染
中度重污染
重度污染
对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间[0,50],(50,100],(100,150],(150,200],(200,250],(250,300]进行分组,得到频率分布直方图如图.
(1)求频率分布直方图中x的值;
(2)计算一年中空气质量分别为良和轻微污染的天数.
解:(1)根据频率分布直方图可知,
x=÷50=.
(2)空气质量为Y的天数=(Y对应的频率÷组距)×组距×365天,所以一年中空气质量为良和轻微污染的天数分别是×50×365=119(天)和×50×365=100(天).
4.某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),下面是这次调查统计分析得到的频率分布表和频率分布直方图(如图所示).
分组
频数
频率
一组
0≤t<5
0
0
二组
5≤t<10
10
0.10
三组
10≤t<15
10
②
四组
15≤t<20
①
0.50
五组
20≤t≤25
30
0.30
合计
100
1.00
解答下列问题:
(1)这次抽样的样本容量是多少?
(2)在表中填写出缺失的数据并补全频率分布直方图;
(3)旅客购票用时的平均数可能落在哪一组?
解:(1)样本容量是100.
(2)①50 ②0.10
所补频率分布直方图如图中的阴影部分:
(3)设旅客平均购票用时为t
min,则有
≤t<
,
即15≤t<20.
所以旅客购票用时的平均数可能落在第四组.
