2.3.2 变量间的相关关系 教案
文档属性
| 名称 | 2.3.2 变量间的相关关系 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 313.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-06 13:14:45 | ||
图片预览


文档简介
2.3
变量间的相关关系
教案
(一)导入新课
思路1
客观事物是相互联系的,过去研究的大多数是因果关系,但实际上更多存在的是一种非因果关系.比如说:某某同学的数学成绩与物理成绩,彼此是互相联系的,但不能认为数学是“因”,物理是“果”,或者反过来说.事实上数学和物理成绩都是“果”,而真正的“因”是学生的理科学习能力和努力程度.所以说,函数关系存在着一种确定性关系,但还存在着另一种非确定性关系——相关关系.为表示这种相关关系,我们接着学习两个变量的线性相关——回归直线及其方程.
思路2
某小卖部为了了解热茶销售量与气温之间的关系,随机统计并制作了某6天卖出热茶的杯数与当天气温的对照表:
气温/℃
26
18
13
10
4
-1
杯数
20
24
34
38
50
64
如果某天的气温是-5
℃,你能根据这些数据预测这天小卖部卖出热茶的杯数吗?为解决这个问题我们接着学习两个变量的线性相关——回归直线及其方程.
(二)推进新课、新知探究、提出问题
(1)作散点图的步骤和方法?
(2)正、负相关的概念?
(3)什么是线性相关?
(4)看人体的脂肪百分比和年龄的散点图,当人的年龄增加时,体内脂肪含量到底是以什么方式增加的呢?
(5)什么叫做回归直线?
(6)如何求回归直线的方程?什么是最小二乘法?它有什么样的思想?
(7)利用计算机如何求回归直线的方程?
(8)利用计算器如何求回归直线的方程?
活动:学生回顾,再思考或讨论,教师及时提示指导.
讨论结果:(1)建立相应的平面直角坐标系,将各数据在平面直角坐标中的对应点画出来,得到表示两个变量的一组数据的图形,这样的图形叫做散点图.(a.如果所有的样本点都落在某一函数曲线上,就用该函数来描述变量之间的关系,即变量之间具有函数关系.b.如果所有的样本点都落在某一函数曲线附近,变量之间就有相关关系.c.如果所有的样本点都落在某一直线附近,变量之间就有线性相关关系)
(2)如果散点图中的点散布在从左下角到右上角的区域内,称为正相关.如果散点图中的点散布在从左上角到右下角的区域内,称为负相关.
(3)如果所有的样本点都落在某一直线附近,变量之间就有线性相关的关系.
(4)大体上来看,随着年龄的增加,人体中脂肪的百分比也在增加,呈正相关的趋势,我们可以从散点图上来进一步分析.
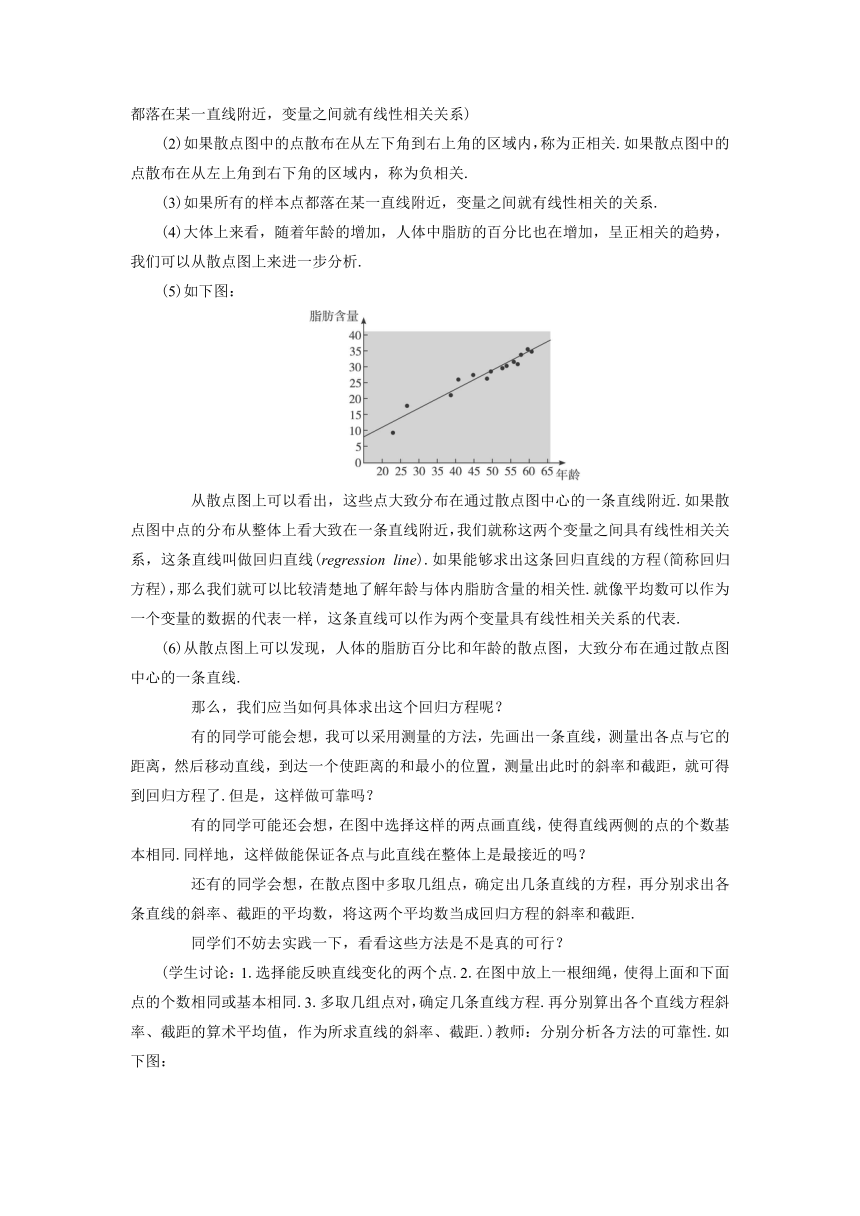
(5)如下图:
从散点图上可以看出,这些点大致分布在通过散点图中心的一条直线附近.如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线叫做回归直线(regression
line).如果能够求出这条回归直线的方程(简称回归方程),那么我们就可以比较清楚地了解年龄与体内脂肪含量的相关性.就像平均数可以作为一个变量的数据的代表一样,这条直线可以作为两个变量具有线性相关关系的代表.
(6)从散点图上可以发现,人体的脂肪百分比和年龄的散点图,大致分布在通过散点图中心的一条直线.
那么,我们应当如何具体求出这个回归方程呢?
有的同学可能会想,我可以采用测量的方法,先画出一条直线,测量出各点与它的距离,然后移动直线,到达一个使距离的和最小的位置,测量出此时的斜率和截距,就可得到回归方程了.但是,这样做可靠吗?
有的同学可能还会想,在图中选择这样的两点画直线,使得直线两侧的点的个数基本相同.同样地,这样做能保证各点与此直线在整体上是最接近的吗?
还有的同学会想,在散点图中多取几组点,确定出几条直线的方程,再分别求出各条直线的斜率、截距的平均数,将这两个平均数当成回归方程的斜率和截距.
同学们不妨去实践一下,看看这些方法是不是真的可行?
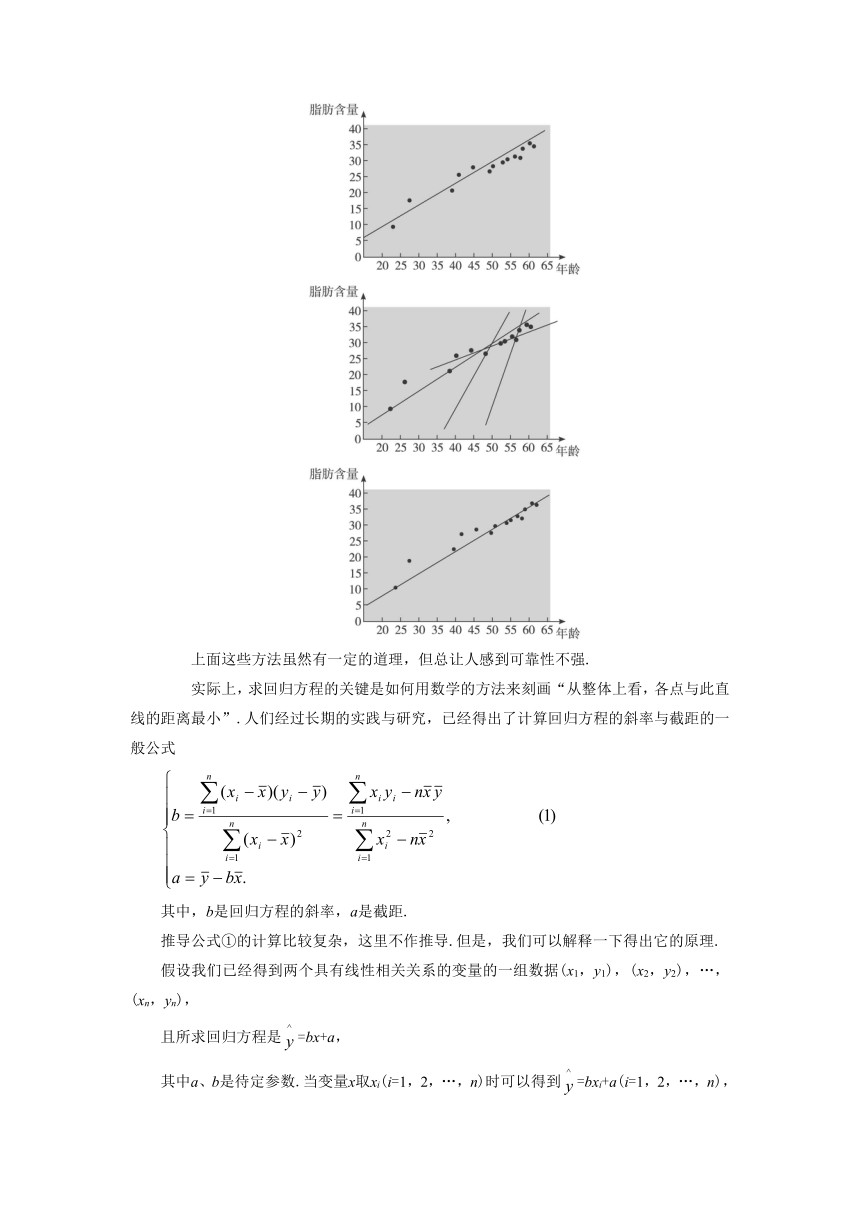
(学生讨论:1.选择能反映直线变化的两个点.2.在图中放上一根细绳,使得上面和下面点的个数相同或基本相同.3.多取几组点对,确定几条直线方程.再分别算出各个直线方程斜率、截距的算术平均值,作为所求直线的斜率、截距.)教师:分别分析各方法的可靠性.如下图:
上面这些方法虽然有一定的道理,但总让人感到可靠性不强.
实际上,求回归方程的关键是如何用数学的方法来刻画“从整体上看,各点与此直线的距离最小”.人们经过长期的实践与研究,已经得出了计算回归方程的斜率与截距的一般公式
其中,b是回归方程的斜率,a是截距.
推导公式①的计算比较复杂,这里不作推导.但是,我们可以解释一下得出它的原理.
假设我们已经得到两个具有线性相关关系的变量的一组数据(x1,y1),(x2,y2),…,(xn,yn),
且所求回归方程是=bx+a,
其中a、b是待定参数.当变量x取xi(i=1,2,…,n)时可以得到=bxi+a(i=1,2,…,n),
它与实际收集到的yi之间的偏差是yi-=yi-(bxi+a)(i=1,2,…,n).
这样,用这n个偏差的和来刻画“各点与此直线的整体偏差”是比较合适的.由于(yi-)可正可负,为了避免相互抵消,可以考虑用来代替,但由于它含有绝对值,运算不太方便,所以改用Q=(y1-bx1-a)2+(y2-bx2-a)2+…+(yn-bxn-a)2
②
来刻画n个点与回归直线在整体上的偏差.
这样,问题就归结为:当a,b取什么值时Q最小,即总体偏差最小.经过数学上求最小值的运算,a,b的值由公式①给出.
通过求②式的最小值而得出回归直线的方法,即求回归直线,使得样本数据的点到它的距离的平方和最小,这一方法叫做最小二乘法(method
of
least
square).
(7)利用计算机求回归直线的方程.
根据最小二乘法的思想和公式①,利用计算器或计算机,可以方便地求出回归方程.
以Excel软件为例,用散点图来建立表示人体的脂肪含量与年龄的相关关系的线性回归方程,具体步骤如下:
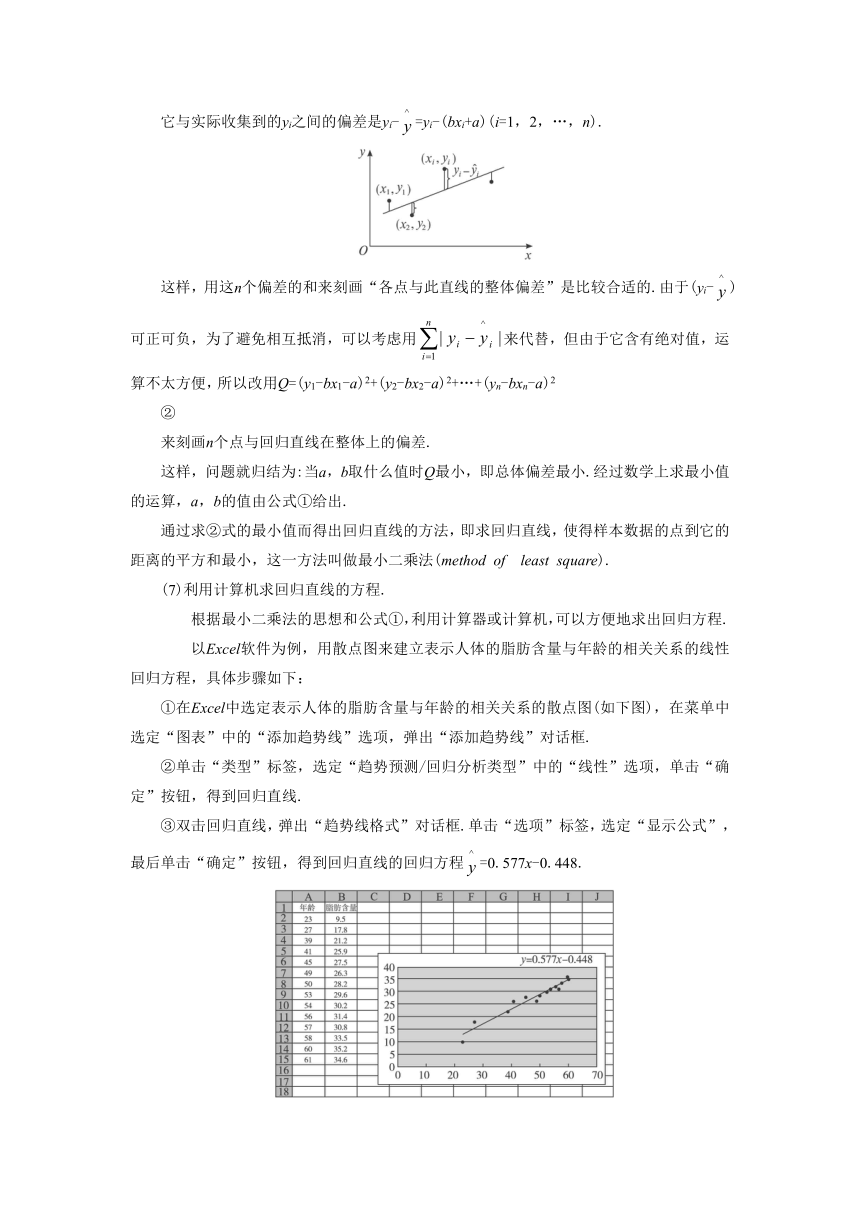
①在Excel中选定表示人体的脂肪含量与年龄的相关关系的散点图(如下图),在菜单中选定“图表”中的“添加趋势线”选项,弹出“添加趋势线”对话框.
②单击“类型”标签,选定“趋势预测/回归分析类型”中的“线性”选项,单击“确定”按钮,得到回归直线.
③双击回归直线,弹出“趋势线格式”对话框.单击“选项”标签,选定“显示公式”,最后单击“确定”按钮,得到回归直线的回归方程=0.577x-0.448.
(8)利用计算器求回归直线的方程.
用计算器求这个回归方程的过程如下:
所以回归方程为=0.577x-0.448.
正像本节开头所说的,我们从人体脂肪含量与年龄这两个变量的一组随机样本数据中,找到了它们之间关系的一个规律,这个规律是由回归直线来反映的.
直线回归方程的应用:
①描述两变量之间的依存关系;利用直线回归方程即可定量描述两个变量间依存的数量关系.
②利用回归方程进行预测;把预报因子(即自变量x)代入回归方程对预报量(即因变量Y)进行估计,即可得到个体Y值的容许区间.
③利用回归方程进行统计控制规定Y值的变化,通过控制x的范围来实现统计控制的目标.如已经得到了空气中NO2的浓度和汽车流量间的回归方程,即可通过控制汽车流量来控制空气中NO2的浓度.
(三)应用示例
思路1
例1
有一个同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的对比表:
摄氏温度/℃
-5
0
4
7
12
15
19
23
27
31
36
热饮杯数
156
150
132
128
130
116
104
89
93
76
54
(1)画出散点图;
(2)从散点图中发现气温与热饮销售杯数之间关系的一般规律;
(3)求回归方程;
(4)如果某天的气温是2
℃,预测这天卖出的热饮杯数.
解:(1)散点图如下图所示:
(2)从上图看到,各点散布在从左上角到右下角的区域里,因此,气温与热饮销售杯数之间呈负相关,即气温越高,卖出去的热饮杯数越少.
(3)从散点图可以看出,这些点大致分布在一条直线的附近,因此,可用公式①求出回归方程的系数.
利用计算器容易求得回归方程=-2.352x+147.767.
(4)当x=2时,=143.063.因此,某天的气温为2
℃时,这天大约可以卖出143杯热饮.
思考
气温为2
℃时,小卖部一定能够卖出143杯左右热饮吗?为什么?
这里的答案是小卖部不一定能够卖出143杯左右热饮,原因如下:
1.线性回归方程中的截距和斜率都是通过样本估计出来的,存在随机误差,这种误差可以导致预测结果的偏差.
2.即使截距和斜率的估计没有误差,也不可能百分之百地保证对应于x的预报值,能够与实际值y很接近.我们不能保证点(x,y)落在回归直线上,甚至不能百分之百地保证它落在回归直线的附近,事实上,y=bx+a+e=+e.
这里e是随机变量,预报值与实际值y的接近程度由随机变量e的标准差所决定.
一些学生可能会提出问题:既然不一定能够卖出143杯左右热饮,那么为什么我们还以“这天大约可以卖出143杯热饮”作为结论呢?这是因为这个结论出现的可能性最大.具体地说,假如我们规定可以选择连续的3个非负整数作为可能的预测结果,则我们选择142,143和144能够保证预测成功(即实际卖出的杯数是这3个数之一)的概率最大.
例2
下表为某地近几年机动车辆数与交通事故数的统计资料.
机动车辆数x/千台
95
110
112
120
129
135
150
180
交通事故数y/千件
6.2
7.5
7.7
8.5
8.7
9.8
10.2
13
(1)请判断机动车辆数与交通事故数之间是否有线性相关关系,如果不具有线性相关关系,说明理由;
(2)如果具有线性相关关系,求出线性回归方程.
解:(1)在直角坐标系中画出数据的散点图,如下图.
直观判断散点在一条直线附近,故具有线性相关关系.
(2)计算相应的数据之和:
=1
031,=71.6,
=137
835,=9
611.7.
将它们代入公式计算得b≈0.077
4,a=-1.024
1,
所以,所求线性回归方程为=0.077
4x-1.024
1.
思路2
例1
给出施化肥量对水稻产量影响的试验数据:
施化肥量x
15
20
25
30
35
40
45
水稻产量y
330
345
365
405
445
450
455
(1)画出上表的散点图;
(2)求出回归直线的方程.
解:(1)散点图如下图.
(2)表中的数据进行具体计算,列成以下表格:
i
1
2
3
4
5
6
7
xi
15
20
25
30
35
40
45
yi
330
345
365
405
445
450
455
xiyi
4
950
6
900
9
125
12
150
15
575
18
000
20
475
故可得到
b=≈4.75,
a=399.3-4.75×30≈257.21世纪教育网
从而得回归直线方程是=4.75x+257.
例2
一个车间为了规定工时定额,需要确定加工零件所花费的时间.为此进行了10次试验,测得数据如下:
零件个数x(个)
10
20
30
40
50
60
70
80
90
100
加工时间y(分)
62
68
75
81
89
95
102
108
115
122
请判断y与x是否具有线性相关关系,如果y与x具有线性相关关系,求线性回归方程.
解:在直角坐标系中画出数据的散点图,如下图.
直观判断散点在一条直线附近,故具有线性相关关系.由测得的数据表可知:
=38
500,=87
777,=55
950.
b=≈0.668.
a==91.7-0.668×55≈54.96.
因此,所求线性回归方程为=bx+a=0.668x+54.96.
例3
已知10条狗的血球体积及红血球数的测量值如下:
血球体积x(mL)
45
42
46
48
42
35
58
40
39
50
红血球数y(百万)
6.53
6.30
9.52
7.50
6.99
5.90
9.49
6.20
6.55
8.72
(1)画出上表的散点图;
(2)求出回归直线的方程.
解:(1)散点图如下.
(2)(45+42+46+48+42+35+58+40+39+50)=44.50,
(6.53+6.30+9.52+7.50+6.99+5.90+9.49+6.20+6.55+8.72)=7.37.
设回归直线方程为=bx+a,则b==0.175,a==-0.418,
所以所求回归直线的方程为=0.175x-0.148.
点评:对一组数据进行线性回归分析时,应先画出其散点图,看其是否呈直线形,再依系数a,b的计算公式,算出a,b.由于计算量较大,所以在计算时应借助技术手段,认真细致,谨防计算中产生错误,求线性回归方程的步骤:计算平均数;计算xi与yi的积,求∑xiyi;计算∑xi2;将结果代入公式求b;用a=求a;写出回归直线方程.
(四)知能训练
1.下列两个变量之间的关系哪个不是函数关系(
)
A.角度和它的余弦值
B.正方形边长和面积
C.正n边形的边数和它的内角和
D.人的年龄和身高
答案:D
2.三点(3,10),(7,20),(11,24)的线性回归方程是(
)
A.=5.75-1.75x
B.=1.75+5.75x
C.=1.75-5.75x
D.=5.75+1.75x
答案:D
3.已知关于某设备的使用年限x与所支出的维修费用y(万元),有如下统计资料:
使用年限x
2
3
4
5
6
维修费用y
2.2
3.8
5.5
6.5
7.0
设y对x呈线性相关关系.试求:
(1)线性回归方程=bx+a的回归系数a,b;
(2)估计使用年限为10年时,维修费用是多少?
答案:(1)b=1.23,a=0.08;(2)12.38.
4.我们考虑两个表示变量x与y之间的关系的模型,δ为误差项,模型如下:
模型1:y=6+4x;模型2:y=6+4x+e.
(1)如果x=3,e=1,分别求两个模型中y的值;
(2)分别说明以上两个模型是确定性模型还是随机模型.
解:(1)模型1:y=6+4x=6+4×3=18;
模型2:y=6+4x+e=6+4×3+1=19.
(2)模型1中相同的x值一定得到相同的y值,所以是确定性模型;模型2中相同的x值,因δ的不同,所得y值不一定相同,且δ为误差项是随机的,所以模型2是随机性模型.
5.以下是收集到的新房屋销售价格y与房屋大小x的数据:
房屋大小x(m2)
80
105
110
115
135
销售价格y(万元)
18.4
22
21.6
24.8
29.2
(1)画出数据的散点图;
(2)用最小二乘法估计求线性回归方程.
解:(1)散点图如下图.
(2)n=5,=545,=109,=116,=23.2,
=60
952,=12
952,
b=≈0.199,a=23.2-0.199×109≈1.509,
所以,线性回归方程为y=0.199x+1.509.
(五)拓展提升
某调查者从调查中获知某公司近年来科研费用支出(Xi)与公司所获得利润(Yi)的统计资料如下表:
科研费用支出(Xi)与利润(Yi)统计表
单位:万元
年份
科研费用支出
利润
199819992000200120022003
5114532
314030342520
合计
30
180
要求估计利润(Yi)对科研费用支出(Xi)的线性回归模型.
解:设线性回归模型直线方程为:,
因为:=5,=30,
根据资料列表计算如下表:
年份
Xi
Yi
XiYi
Xi2
Xi-
Yi-
(Xi-)2
(Xi-)(Yi-)
199819992000200120022003
5114532
314030342520
1554401201707540
25121162594
06-10-2-3
11004-5-10
0361049
060001030
合计
30
180
1
000
200
0
0
50
100
现求解参数β0、β1的估计值:
方法一:=2,
=30-2×5=20.
方法二:=2,
=30-2×5=20.
方法三:=2,
=30-2×5=20.
所以利润(Yi)对科研费用支出(Xi)的线性回归模型直线方程为:=20+2Xi.
(六)课堂小结
1.求线性回归方程的步骤:
(1)计算平均数;
(2)计算xi与yi的积,求∑xiyi;
(3)计算∑xi2,∑yi2,
(4)将上述有关结果代入公式
求b,a,写出回归直线方程.
2.经历用不同估算方法描述两个变量线性相关的过程.知道最小二乘法的思想,能根据给出的线性回归方程系数公式建立线性回归方程.
(七)作业
习题2.3A组3、4,B组1、2.
变量间的相关关系
教案
(一)导入新课
思路1
客观事物是相互联系的,过去研究的大多数是因果关系,但实际上更多存在的是一种非因果关系.比如说:某某同学的数学成绩与物理成绩,彼此是互相联系的,但不能认为数学是“因”,物理是“果”,或者反过来说.事实上数学和物理成绩都是“果”,而真正的“因”是学生的理科学习能力和努力程度.所以说,函数关系存在着一种确定性关系,但还存在着另一种非确定性关系——相关关系.为表示这种相关关系,我们接着学习两个变量的线性相关——回归直线及其方程.
思路2
某小卖部为了了解热茶销售量与气温之间的关系,随机统计并制作了某6天卖出热茶的杯数与当天气温的对照表:
气温/℃
26
18
13
10
4
-1
杯数
20
24
34
38
50
64
如果某天的气温是-5
℃,你能根据这些数据预测这天小卖部卖出热茶的杯数吗?为解决这个问题我们接着学习两个变量的线性相关——回归直线及其方程.
(二)推进新课、新知探究、提出问题
(1)作散点图的步骤和方法?
(2)正、负相关的概念?
(3)什么是线性相关?
(4)看人体的脂肪百分比和年龄的散点图,当人的年龄增加时,体内脂肪含量到底是以什么方式增加的呢?
(5)什么叫做回归直线?
(6)如何求回归直线的方程?什么是最小二乘法?它有什么样的思想?
(7)利用计算机如何求回归直线的方程?
(8)利用计算器如何求回归直线的方程?
活动:学生回顾,再思考或讨论,教师及时提示指导.
讨论结果:(1)建立相应的平面直角坐标系,将各数据在平面直角坐标中的对应点画出来,得到表示两个变量的一组数据的图形,这样的图形叫做散点图.(a.如果所有的样本点都落在某一函数曲线上,就用该函数来描述变量之间的关系,即变量之间具有函数关系.b.如果所有的样本点都落在某一函数曲线附近,变量之间就有相关关系.c.如果所有的样本点都落在某一直线附近,变量之间就有线性相关关系)
(2)如果散点图中的点散布在从左下角到右上角的区域内,称为正相关.如果散点图中的点散布在从左上角到右下角的区域内,称为负相关.
(3)如果所有的样本点都落在某一直线附近,变量之间就有线性相关的关系.
(4)大体上来看,随着年龄的增加,人体中脂肪的百分比也在增加,呈正相关的趋势,我们可以从散点图上来进一步分析.
(5)如下图:
从散点图上可以看出,这些点大致分布在通过散点图中心的一条直线附近.如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线叫做回归直线(regression
line).如果能够求出这条回归直线的方程(简称回归方程),那么我们就可以比较清楚地了解年龄与体内脂肪含量的相关性.就像平均数可以作为一个变量的数据的代表一样,这条直线可以作为两个变量具有线性相关关系的代表.
(6)从散点图上可以发现,人体的脂肪百分比和年龄的散点图,大致分布在通过散点图中心的一条直线.
那么,我们应当如何具体求出这个回归方程呢?
有的同学可能会想,我可以采用测量的方法,先画出一条直线,测量出各点与它的距离,然后移动直线,到达一个使距离的和最小的位置,测量出此时的斜率和截距,就可得到回归方程了.但是,这样做可靠吗?
有的同学可能还会想,在图中选择这样的两点画直线,使得直线两侧的点的个数基本相同.同样地,这样做能保证各点与此直线在整体上是最接近的吗?
还有的同学会想,在散点图中多取几组点,确定出几条直线的方程,再分别求出各条直线的斜率、截距的平均数,将这两个平均数当成回归方程的斜率和截距.
同学们不妨去实践一下,看看这些方法是不是真的可行?
(学生讨论:1.选择能反映直线变化的两个点.2.在图中放上一根细绳,使得上面和下面点的个数相同或基本相同.3.多取几组点对,确定几条直线方程.再分别算出各个直线方程斜率、截距的算术平均值,作为所求直线的斜率、截距.)教师:分别分析各方法的可靠性.如下图:
上面这些方法虽然有一定的道理,但总让人感到可靠性不强.
实际上,求回归方程的关键是如何用数学的方法来刻画“从整体上看,各点与此直线的距离最小”.人们经过长期的实践与研究,已经得出了计算回归方程的斜率与截距的一般公式
其中,b是回归方程的斜率,a是截距.
推导公式①的计算比较复杂,这里不作推导.但是,我们可以解释一下得出它的原理.
假设我们已经得到两个具有线性相关关系的变量的一组数据(x1,y1),(x2,y2),…,(xn,yn),
且所求回归方程是=bx+a,
其中a、b是待定参数.当变量x取xi(i=1,2,…,n)时可以得到=bxi+a(i=1,2,…,n),
它与实际收集到的yi之间的偏差是yi-=yi-(bxi+a)(i=1,2,…,n).
这样,用这n个偏差的和来刻画“各点与此直线的整体偏差”是比较合适的.由于(yi-)可正可负,为了避免相互抵消,可以考虑用来代替,但由于它含有绝对值,运算不太方便,所以改用Q=(y1-bx1-a)2+(y2-bx2-a)2+…+(yn-bxn-a)2
②
来刻画n个点与回归直线在整体上的偏差.
这样,问题就归结为:当a,b取什么值时Q最小,即总体偏差最小.经过数学上求最小值的运算,a,b的值由公式①给出.
通过求②式的最小值而得出回归直线的方法,即求回归直线,使得样本数据的点到它的距离的平方和最小,这一方法叫做最小二乘法(method
of
least
square).
(7)利用计算机求回归直线的方程.
根据最小二乘法的思想和公式①,利用计算器或计算机,可以方便地求出回归方程.
以Excel软件为例,用散点图来建立表示人体的脂肪含量与年龄的相关关系的线性回归方程,具体步骤如下:
①在Excel中选定表示人体的脂肪含量与年龄的相关关系的散点图(如下图),在菜单中选定“图表”中的“添加趋势线”选项,弹出“添加趋势线”对话框.
②单击“类型”标签,选定“趋势预测/回归分析类型”中的“线性”选项,单击“确定”按钮,得到回归直线.
③双击回归直线,弹出“趋势线格式”对话框.单击“选项”标签,选定“显示公式”,最后单击“确定”按钮,得到回归直线的回归方程=0.577x-0.448.
(8)利用计算器求回归直线的方程.
用计算器求这个回归方程的过程如下:
所以回归方程为=0.577x-0.448.
正像本节开头所说的,我们从人体脂肪含量与年龄这两个变量的一组随机样本数据中,找到了它们之间关系的一个规律,这个规律是由回归直线来反映的.
直线回归方程的应用:
①描述两变量之间的依存关系;利用直线回归方程即可定量描述两个变量间依存的数量关系.
②利用回归方程进行预测;把预报因子(即自变量x)代入回归方程对预报量(即因变量Y)进行估计,即可得到个体Y值的容许区间.
③利用回归方程进行统计控制规定Y值的变化,通过控制x的范围来实现统计控制的目标.如已经得到了空气中NO2的浓度和汽车流量间的回归方程,即可通过控制汽车流量来控制空气中NO2的浓度.
(三)应用示例
思路1
例1
有一个同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的对比表:
摄氏温度/℃
-5
0
4
7
12
15
19
23
27
31
36
热饮杯数
156
150
132
128
130
116
104
89
93
76
54
(1)画出散点图;
(2)从散点图中发现气温与热饮销售杯数之间关系的一般规律;
(3)求回归方程;
(4)如果某天的气温是2
℃,预测这天卖出的热饮杯数.
解:(1)散点图如下图所示:
(2)从上图看到,各点散布在从左上角到右下角的区域里,因此,气温与热饮销售杯数之间呈负相关,即气温越高,卖出去的热饮杯数越少.
(3)从散点图可以看出,这些点大致分布在一条直线的附近,因此,可用公式①求出回归方程的系数.
利用计算器容易求得回归方程=-2.352x+147.767.
(4)当x=2时,=143.063.因此,某天的气温为2
℃时,这天大约可以卖出143杯热饮.
思考
气温为2
℃时,小卖部一定能够卖出143杯左右热饮吗?为什么?
这里的答案是小卖部不一定能够卖出143杯左右热饮,原因如下:
1.线性回归方程中的截距和斜率都是通过样本估计出来的,存在随机误差,这种误差可以导致预测结果的偏差.
2.即使截距和斜率的估计没有误差,也不可能百分之百地保证对应于x的预报值,能够与实际值y很接近.我们不能保证点(x,y)落在回归直线上,甚至不能百分之百地保证它落在回归直线的附近,事实上,y=bx+a+e=+e.
这里e是随机变量,预报值与实际值y的接近程度由随机变量e的标准差所决定.
一些学生可能会提出问题:既然不一定能够卖出143杯左右热饮,那么为什么我们还以“这天大约可以卖出143杯热饮”作为结论呢?这是因为这个结论出现的可能性最大.具体地说,假如我们规定可以选择连续的3个非负整数作为可能的预测结果,则我们选择142,143和144能够保证预测成功(即实际卖出的杯数是这3个数之一)的概率最大.
例2
下表为某地近几年机动车辆数与交通事故数的统计资料.
机动车辆数x/千台
95
110
112
120
129
135
150
180
交通事故数y/千件
6.2
7.5
7.7
8.5
8.7
9.8
10.2
13
(1)请判断机动车辆数与交通事故数之间是否有线性相关关系,如果不具有线性相关关系,说明理由;
(2)如果具有线性相关关系,求出线性回归方程.
解:(1)在直角坐标系中画出数据的散点图,如下图.
直观判断散点在一条直线附近,故具有线性相关关系.
(2)计算相应的数据之和:
=1
031,=71.6,
=137
835,=9
611.7.
将它们代入公式计算得b≈0.077
4,a=-1.024
1,
所以,所求线性回归方程为=0.077
4x-1.024
1.
思路2
例1
给出施化肥量对水稻产量影响的试验数据:
施化肥量x
15
20
25
30
35
40
45
水稻产量y
330
345
365
405
445
450
455
(1)画出上表的散点图;
(2)求出回归直线的方程.
解:(1)散点图如下图.
(2)表中的数据进行具体计算,列成以下表格:
i
1
2
3
4
5
6
7
xi
15
20
25
30
35
40
45
yi
330
345
365
405
445
450
455
xiyi
4
950
6
900
9
125
12
150
15
575
18
000
20
475
故可得到
b=≈4.75,
a=399.3-4.75×30≈257.21世纪教育网
从而得回归直线方程是=4.75x+257.
例2
一个车间为了规定工时定额,需要确定加工零件所花费的时间.为此进行了10次试验,测得数据如下:
零件个数x(个)
10
20
30
40
50
60
70
80
90
100
加工时间y(分)
62
68
75
81
89
95
102
108
115
122
请判断y与x是否具有线性相关关系,如果y与x具有线性相关关系,求线性回归方程.
解:在直角坐标系中画出数据的散点图,如下图.
直观判断散点在一条直线附近,故具有线性相关关系.由测得的数据表可知:
=38
500,=87
777,=55
950.
b=≈0.668.
a==91.7-0.668×55≈54.96.
因此,所求线性回归方程为=bx+a=0.668x+54.96.
例3
已知10条狗的血球体积及红血球数的测量值如下:
血球体积x(mL)
45
42
46
48
42
35
58
40
39
50
红血球数y(百万)
6.53
6.30
9.52
7.50
6.99
5.90
9.49
6.20
6.55
8.72
(1)画出上表的散点图;
(2)求出回归直线的方程.
解:(1)散点图如下.
(2)(45+42+46+48+42+35+58+40+39+50)=44.50,
(6.53+6.30+9.52+7.50+6.99+5.90+9.49+6.20+6.55+8.72)=7.37.
设回归直线方程为=bx+a,则b==0.175,a==-0.418,
所以所求回归直线的方程为=0.175x-0.148.
点评:对一组数据进行线性回归分析时,应先画出其散点图,看其是否呈直线形,再依系数a,b的计算公式,算出a,b.由于计算量较大,所以在计算时应借助技术手段,认真细致,谨防计算中产生错误,求线性回归方程的步骤:计算平均数;计算xi与yi的积,求∑xiyi;计算∑xi2;将结果代入公式求b;用a=求a;写出回归直线方程.
(四)知能训练
1.下列两个变量之间的关系哪个不是函数关系(
)
A.角度和它的余弦值
B.正方形边长和面积
C.正n边形的边数和它的内角和
D.人的年龄和身高
答案:D
2.三点(3,10),(7,20),(11,24)的线性回归方程是(
)
A.=5.75-1.75x
B.=1.75+5.75x
C.=1.75-5.75x
D.=5.75+1.75x
答案:D
3.已知关于某设备的使用年限x与所支出的维修费用y(万元),有如下统计资料:
使用年限x
2
3
4
5
6
维修费用y
2.2
3.8
5.5
6.5
7.0
设y对x呈线性相关关系.试求:
(1)线性回归方程=bx+a的回归系数a,b;
(2)估计使用年限为10年时,维修费用是多少?
答案:(1)b=1.23,a=0.08;(2)12.38.
4.我们考虑两个表示变量x与y之间的关系的模型,δ为误差项,模型如下:
模型1:y=6+4x;模型2:y=6+4x+e.
(1)如果x=3,e=1,分别求两个模型中y的值;
(2)分别说明以上两个模型是确定性模型还是随机模型.
解:(1)模型1:y=6+4x=6+4×3=18;
模型2:y=6+4x+e=6+4×3+1=19.
(2)模型1中相同的x值一定得到相同的y值,所以是确定性模型;模型2中相同的x值,因δ的不同,所得y值不一定相同,且δ为误差项是随机的,所以模型2是随机性模型.
5.以下是收集到的新房屋销售价格y与房屋大小x的数据:
房屋大小x(m2)
80
105
110
115
135
销售价格y(万元)
18.4
22
21.6
24.8
29.2
(1)画出数据的散点图;
(2)用最小二乘法估计求线性回归方程.
解:(1)散点图如下图.
(2)n=5,=545,=109,=116,=23.2,
=60
952,=12
952,
b=≈0.199,a=23.2-0.199×109≈1.509,
所以,线性回归方程为y=0.199x+1.509.
(五)拓展提升
某调查者从调查中获知某公司近年来科研费用支出(Xi)与公司所获得利润(Yi)的统计资料如下表:
科研费用支出(Xi)与利润(Yi)统计表
单位:万元
年份
科研费用支出
利润
199819992000200120022003
5114532
314030342520
合计
30
180
要求估计利润(Yi)对科研费用支出(Xi)的线性回归模型.
解:设线性回归模型直线方程为:,
因为:=5,=30,
根据资料列表计算如下表:
年份
Xi
Yi
XiYi
Xi2
Xi-
Yi-
(Xi-)2
(Xi-)(Yi-)
199819992000200120022003
5114532
314030342520
1554401201707540
25121162594
06-10-2-3
11004-5-10
0361049
060001030
合计
30
180
1
000
200
0
0
50
100
现求解参数β0、β1的估计值:
方法一:=2,
=30-2×5=20.
方法二:=2,
=30-2×5=20.
方法三:=2,
=30-2×5=20.
所以利润(Yi)对科研费用支出(Xi)的线性回归模型直线方程为:=20+2Xi.
(六)课堂小结
1.求线性回归方程的步骤:
(1)计算平均数;
(2)计算xi与yi的积,求∑xiyi;
(3)计算∑xi2,∑yi2,
(4)将上述有关结果代入公式
求b,a,写出回归直线方程.
2.经历用不同估算方法描述两个变量线性相关的过程.知道最小二乘法的思想,能根据给出的线性回归方程系数公式建立线性回归方程.
(七)作业
习题2.3A组3、4,B组1、2.
