12.2 一次函数 第5课时 利用一次函数进行方案决策【同步练习】
文档属性
| 名称 | 12.2 一次函数 第5课时 利用一次函数进行方案决策【同步练习】 |

|
|
| 格式 | zip | ||
| 文件大小 | 38.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-05 18:51:43 | ||
图片预览

文档简介
第5课时
利用一次函数进行方案决策
1.
点A(-5,),B()都在直线上,则与的大小关系是(
)
A.
B.
C.
D.
2.
函数与x轴交点的横坐标是(
)
A.
–3
B.
6
C.
3
D.
–6
3.
已知点(2,-1)是方程的一个解,则直线的图象不经过的象限有(
)
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
4.
已知一次函数,当时,的取值范围是____________.当时,x的值为_________,当时,x的取值范围是__________.
5.
若函数的图象在x轴上方,则x的取值范围是_________.
6.
画出函数的图象,利用图象求
(1)方程的根.(2)不等式的解集.
(3)当时,求x的取值范围.
(4)当时,求x的取值范围.
(5)求直线与坐标轴围成的三角形的面积.
7.
某实验田里的农作物每天的需水量y()与生长时间x(天)之间的关系如折线图所示.这些农作物在第10天,第30天的需水量分别为2000kg和3000kg,在第40天后每天的需水量比前一天增加了100kg.
(1)分别求出和时y与x之间的函数关系式.
(2)如果这些农作物每天的需水量大于或等于4000kg时,需要进行人工灌溉,那么应从第几天开始进行人工灌溉?
8.
小明准备将平时的零用钱节约一些储存起来,他已存有50元,从现在起每个月存12元.
(1)试写出小明的存款数与从现在开始的月份数之间的函数关系式.
(2)小明的同学小丽以前没有存过零用钱,听说小明存零用钱,她表示从现在起每个月存18元,争取超过小明,半年后小丽的存款数是多少?能否超过小明?至少几个月后小丽的存款数超过小明?
9.
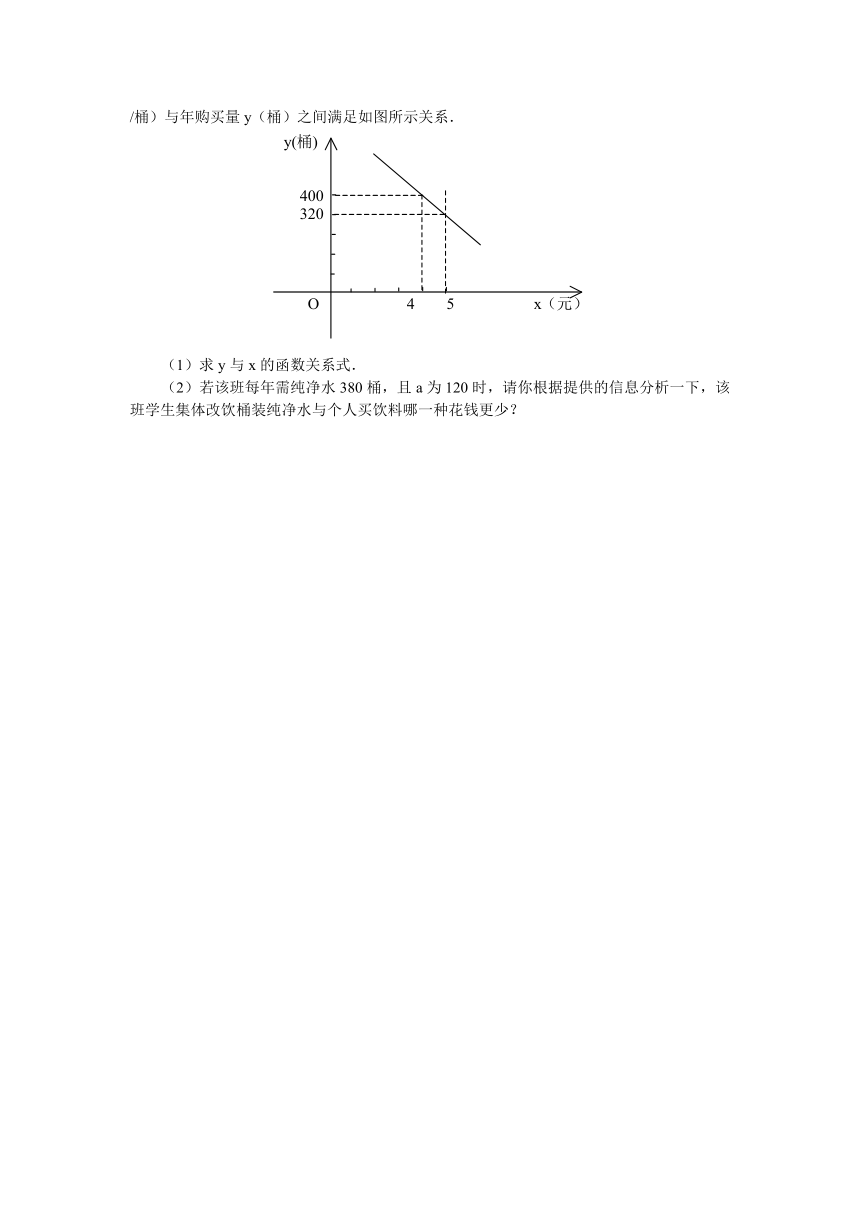
某校八年级(1)班共有学生50人,据统计原来每人每年用于购买饮料的平均支出是a元,经测算和市场调查,若该班学生集体改饮某品牌的桶装纯净水,则年总费用由两部分组成,一部分是购买纯净水的费用,另一部分是其他费用780元.其中,纯净水的销售价x(元/桶)与年购买量y(桶)之间满足如图所示关系.
(1)求y与x的函数关系式.
(2)若该班每年需纯净水380桶,且a为120时,请你根据提供的信息分析一下,该班学生集体改饮桶装纯净水与个人买饮料哪一种花钱更少?
【试题答案】
1.
是y随x的增大而减小,,,选D.
2.
,选D
3.
(2,-1)是方程的解,
图象经过一、二、四象限,选C.
4.
;;
5.
即时x的范围.
6.
列表
x
0
1
y
1
3
描点
连线
(1)
(2)
(3)
(4)
(5)
7.
(1)根据图象用待定系数法.(2)当时解一元一次不等式可解决问题.
(1)当时,设,根据题意
解方程组得,所以时,与x之间的关系式为
所以当时,
当时,由题意,
即
(2)当时,y与x之间的关系式为
解不等式,得
所以应从第45天起进行人工灌溉.
8.
(1)设小明的存款数为,从现在起存款月份为x,
则
(2)设小丽的存款数为,则
当时,
,
半年后小丽的存款数不能超过小明.
当时,即,即
至少9个月后小丽的存款数超过小明.
9.
(1)设,由图象知时,时,,所以解得
所以y与x的解析式为
(2)该班学生买饮料每年总费用(元)
当时,得解得
该班学生集体饮用桶装纯净水的每年总费用为(元).所以,显然从经济上看饮用桶装纯净水花钱少.
利用一次函数进行方案决策
1.
点A(-5,),B()都在直线上,则与的大小关系是(
)
A.
B.
C.
D.
2.
函数与x轴交点的横坐标是(
)
A.
–3
B.
6
C.
3
D.
–6
3.
已知点(2,-1)是方程的一个解,则直线的图象不经过的象限有(
)
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
4.
已知一次函数,当时,的取值范围是____________.当时,x的值为_________,当时,x的取值范围是__________.
5.
若函数的图象在x轴上方,则x的取值范围是_________.
6.
画出函数的图象,利用图象求
(1)方程的根.(2)不等式的解集.
(3)当时,求x的取值范围.
(4)当时,求x的取值范围.
(5)求直线与坐标轴围成的三角形的面积.
7.
某实验田里的农作物每天的需水量y()与生长时间x(天)之间的关系如折线图所示.这些农作物在第10天,第30天的需水量分别为2000kg和3000kg,在第40天后每天的需水量比前一天增加了100kg.
(1)分别求出和时y与x之间的函数关系式.
(2)如果这些农作物每天的需水量大于或等于4000kg时,需要进行人工灌溉,那么应从第几天开始进行人工灌溉?
8.
小明准备将平时的零用钱节约一些储存起来,他已存有50元,从现在起每个月存12元.
(1)试写出小明的存款数与从现在开始的月份数之间的函数关系式.
(2)小明的同学小丽以前没有存过零用钱,听说小明存零用钱,她表示从现在起每个月存18元,争取超过小明,半年后小丽的存款数是多少?能否超过小明?至少几个月后小丽的存款数超过小明?
9.
某校八年级(1)班共有学生50人,据统计原来每人每年用于购买饮料的平均支出是a元,经测算和市场调查,若该班学生集体改饮某品牌的桶装纯净水,则年总费用由两部分组成,一部分是购买纯净水的费用,另一部分是其他费用780元.其中,纯净水的销售价x(元/桶)与年购买量y(桶)之间满足如图所示关系.
(1)求y与x的函数关系式.
(2)若该班每年需纯净水380桶,且a为120时,请你根据提供的信息分析一下,该班学生集体改饮桶装纯净水与个人买饮料哪一种花钱更少?
【试题答案】
1.
是y随x的增大而减小,,,选D.
2.
,选D
3.
(2,-1)是方程的解,
图象经过一、二、四象限,选C.
4.
;;
5.
即时x的范围.
6.
列表
x
0
1
y
1
3
描点
连线
(1)
(2)
(3)
(4)
(5)
7.
(1)根据图象用待定系数法.(2)当时解一元一次不等式可解决问题.
(1)当时,设,根据题意
解方程组得,所以时,与x之间的关系式为
所以当时,
当时,由题意,
即
(2)当时,y与x之间的关系式为
解不等式,得
所以应从第45天起进行人工灌溉.
8.
(1)设小明的存款数为,从现在起存款月份为x,
则
(2)设小丽的存款数为,则
当时,
,
半年后小丽的存款数不能超过小明.
当时,即,即
至少9个月后小丽的存款数超过小明.
9.
(1)设,由图象知时,时,,所以解得
所以y与x的解析式为
(2)该班学生买饮料每年总费用(元)
当时,得解得
该班学生集体饮用桶装纯净水的每年总费用为(元).所以,显然从经济上看饮用桶装纯净水花钱少.
