七年级上数学第四章一元一次方程复习试卷(含答案)
文档属性
| 名称 | 七年级上数学第四章一元一次方程复习试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 94.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-06 22:19:14 | ||
图片预览


文档简介
第四章《一元一次方程》复习卷
(满分:100分
时间:90分钟)
一、选择题
(每题2分,共16分)
1.下列结论不能由a+b=0得到的是
(
)
A.a
2=-a
b
B.=
C.a
=0,b
=0
D.a2=b2
2.若代数式x+4的值是2,则x等于
(
)
A.2
B.-2
C.6
D.-6
3.若关于x的方程2
x-a-5=0的解是x=-2,则a的值为
(
)
A.1
B.-1
C.9
D.-9
4.在解方程-=1时,去分母正确的是
(
)
A.3(x-1)-2(2+3x)=1
B.3(x-1)+2(2x+3)=1
C.3(x-1)+2(2+3x)=6
D.3(x-1)-2(2x+3)=6
5.小明在做解方程作业时,不小心将方程中的一个常数污染了,看不清楚,被污染的方程是2y-=y-
怎么办呢
小明想了一想,便翻看书后答案,此方程的解是y=-,于是很快就补好了这个常数,你能补出这个常数吗
它应是
(
)
A.4
B.3
C.2
D.1
6.小明在日历的某月上圈出五个数,呈十字框形,若它们的和是55,则中间的数是
(
)
A.9
B.10
C.11
D.12
7.小郑的年龄比妈妈小28岁,今年妈妈的年龄正好是小郑的5倍.小郑今年的年龄是
(
)
A.7岁
B.8岁
C.9岁
D.10岁
8.已知面包店的面包一个15元,小明去此
( http: / / www.21cnjy.com )店买面包,结账时店员告诉小明:“如果你再多买一个面包就可以打九折,价钱会比现在便宜45元.”小明说:“我买这些就好了,谢谢.”根据两人的对话,判断结账时小明买的面包个数是
(
)
A.38
B.39
C.40
D.41
二、填空题
(每题2分,共20分)
9.若3x-5=0,则5x-3=
.
10.当m=
时,方程2x+m=x+l的解为x=-4.
11.若4x2m-1
y
n与-xy2是同类项,则m+n=
.
12.当y=
时,代数式2(3y+4)的值比5
(2y-7)
的值大3.
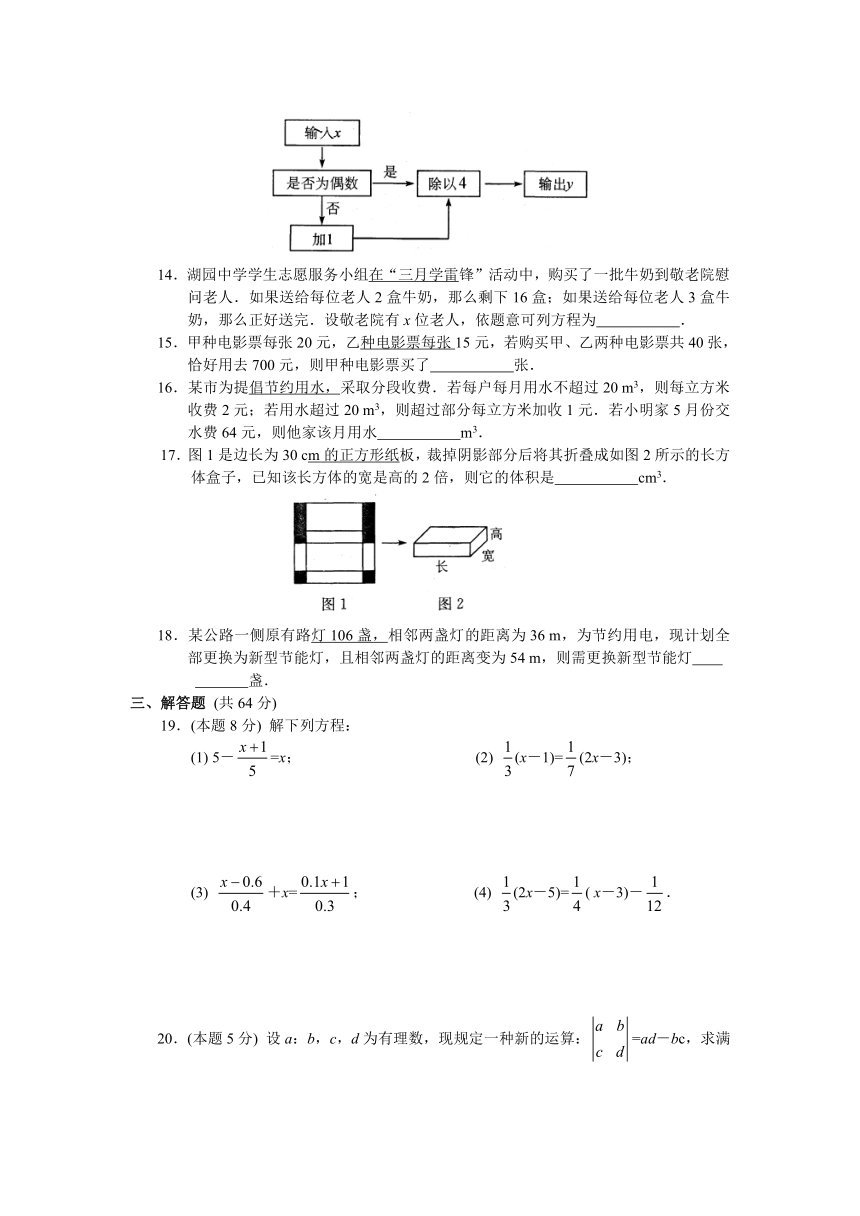
13.在如图所示的运算程序中,若输出的数y=7,则输入的数x=
.
( http: / / www.21cnjy.com )
14.湖园中学学生志愿服务小组在“三月学雷
( http: / / www.21cnjy.com )锋”活动中,购买了一批牛奶到敬老院慰问老人.如果送给每位老人2盒牛奶,那么剩下16盒;如果送给每位老人3盒牛奶,那么正好送完.设敬老院有x位老人,依题意可列方程为
.
15.甲种电影票每张20元,乙种电影票每张
( http: / / www.21cnjy.com )15元,若购买甲、乙两种电影票共40张,恰好用去700元,则甲种电影票买了
张.
16.某市为提倡节约用水,
( http: / / www.21cnjy.com )采取分段收费.若每户每月用水不超过20
m3,则每立方米收费2元;若用水超过20
m3,则超过部分每立方米加收1元.若小明家5月份交水费64元,则他家该月用水
m3.
17.图1是边长为30
cm的正方形纸
( http: / / www.21cnjy.com )板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知该长方体的宽是高的2倍,则它的体积是
cm3.
( http: / / www.21cnjy.com )
18.某公路一侧原有路灯106盏,
( http: / / www.21cnjy.com )相邻两盏灯的距离为36
m,为节约用电,现计划全部更换为新型节能灯,且相邻两盏灯的距离变为54
m,则需更换新型节能灯
盏.
三、解答题
(共64分)
19.(本题8分)
解下列方程:
(1)
5-=x;
(2)
(x-1)=(2x-3);
(3)
+x=;
(4)
(2x-5)=(
x-3)-.
20.(本题5分)
设a:b,c,d为有理数,现规定一种新的运算:=ad-bc,求满足等式=1的x的值.
21.(本题5分)
当m为何值时,关于x的方程5m+3x=1+x的解比关于x的方程2x+m=3m的解大2
22.(本题5分)
如果代数式的值比的值多1,求a-2的值.
23.(本题5分)
若关于x的方程=2+无论k为何值,方程的解总是x=1,求a,b的值.
24.(本题6分)
把一些图书分给某班学生阅读,若每人分3本,则剩余20本;若每人分4本,则还缺25本.这个班有多少名学生
25.(本题8分)
某一天,一蔬菜
( http: / / www.21cnjy.com )经营户用114元从蔬菜批发市场购进黄瓜和土豆共40
kg到菜市场去卖.黄瓜和土豆这一天的批发价和零售价
(单位:元/kg)如下表所示:
( http: / / www.21cnjy.com )
(1)
他当天购进了黄瓜和土豆各多少千克
(2)
如果黄瓜和土豆全部卖完,他能赚多少钱
26.(本题8分)
李华早上骑自行车上学,中
( http: / / www.21cnjy.com )途因道路施工推车步行了一段路,到学校共用时15
min,如果他骑自行车的平均速度是每分钟250
m,推车步行的平均速度是每分钟80
m,他家离学校的路程是2900
m,求他推车步行的时间.
27.(本题12分)
某景
( http: / / www.21cnjy.com )区内的环形路是边长为800
m的正方形ABCD,如图1和图2所示.现有1号、2号两游览车分别从出口A和景点C同时出发,1号车逆时针、2号车逆时针沿环形路连续循环行驶,供游客随时免费乘车
(上、下车的时间忽略不计),两车速度均为200
m/min.
( http: / / www.21cnjy.com )
[探究]设行驶时间为t
min.
(1)
当0≤t≤8时,
( http: / / www.21cnjy.com )分别用含t的代数式表示1号车、2号车在左半环线离出口A的路程y1,y2
(m),并求出当两车相距的路程是400
m时t的值;
(2)
求当t为何值时,1号车第三次恰好经过景点C,并直接写出这一段时间内它与2号车相遇过的次数.
[发现]
如图2,游客甲在BC上的一点K
(不与点B,C重合)
处候车,准备乘车到出口A.
设CK=x
m.
情况一:若他刚好错过2号车,便搭乘即将到来的1号车;
情况二:若他刚好错过1号车,便搭乘即将到来的2号车.
比较哪种情况用时较多.(含候车时间)
参考答案
一、选择题
1.C
2.B
3.D
4.D
5.B
6.C
7.A
8.B
二、填空题
9.
10.5
11.3
12.10
13.27或28
14.2x+16=3x
15.20
16.28
17.1000
18.71
三、解答题
19.(1)
x=4
(2)
x=-2
(3)
x=
(4)
x=2
20.由题意得-×2=1,则x=-10
21.方程5m+3x=1+x的解是x=,方程2x+m=3m的解是x=m.由题意可知-m=2,解得m=-,即当m=-时,关于x的方程5m+3x=1+x的解比关于x的方程2x+m=3m的解大2
22.由题意得-=1,解得a=5,则a-2的值为3
23.方程两边同时乘以6得4kx+2a=12+x-bk,即(4k-1)
x+2a+bk-12=0
①.因为无论k为何值时,它的解总是1,所以把x=1代入①,得4k-1+2a+bk-12=k(4+b)-13+2a=0,所以4+b=0,-13+2a=0,即b=-4,a=
24.设这个班有x名学生,根据题意得3x+20=4x-25,解得x=45.答:这个班共有45名学生
25.(1)
设购进黄瓜x
kg,则购
( http: / / www.21cnjy.com )进土豆(40-x)
kg,根据题意得2.4x+3(40-x)=114,解得x=10,则40-x=30.答:他购进黄瓜10
kg,购进土豆30
kg
(2)
他能赚10×(4-2.4)+30×(5-3)=76
(元)
26.设他推车步行了x
min,依题意得80x+250(15-x)=2900,解得x=5.答:他推车步行了5
min
27.(1)
y1=200t(0≤t≤8)
y2=1600-200t(0≤t≤8)
当两车相距路程为400
m时,应分两种情况:①当未相遇前,两车相距路程为400
m,则有200t+200t+400=2×800,解得t=3.即当t=3时,两车相距的路程为400
m.
②当相遇之后,两车相距路程为400
m,则有200t+200t=2×800+400,解得t=5.即当t=5时,两车相距的路程为400
m综上所得,当t=3或5时,两车相距的路程为400
m
(2)
当1号车第三次恰好经过景点C时,它已经从A点开始绕正方形2圈半,则可知2×800×4+800×2=200t,解得t=40.即t=40时,1号车第三次恰好经过景点C,且这段时间内它与2号车相遇了5次.[发现]情况一:若他刚好错过2号车,便搭乘即将到来的1号车时,从开始等车到到达出口A,所用时间为
(+)
min,即(16-)
min;情况二:若他刚好错过1号车,便搭乘即将到来的2号车时,从开始等车到到达出口A,所用时间为
(+)
min.即(16+)
min因为16-<16+(
x>0),所以情况二用时较多
(满分:100分
时间:90分钟)
一、选择题
(每题2分,共16分)
1.下列结论不能由a+b=0得到的是
(
)
A.a
2=-a
b
B.=
C.a
=0,b
=0
D.a2=b2
2.若代数式x+4的值是2,则x等于
(
)
A.2
B.-2
C.6
D.-6
3.若关于x的方程2
x-a-5=0的解是x=-2,则a的值为
(
)
A.1
B.-1
C.9
D.-9
4.在解方程-=1时,去分母正确的是
(
)
A.3(x-1)-2(2+3x)=1
B.3(x-1)+2(2x+3)=1
C.3(x-1)+2(2+3x)=6
D.3(x-1)-2(2x+3)=6
5.小明在做解方程作业时,不小心将方程中的一个常数污染了,看不清楚,被污染的方程是2y-=y-
怎么办呢
小明想了一想,便翻看书后答案,此方程的解是y=-,于是很快就补好了这个常数,你能补出这个常数吗
它应是
(
)
A.4
B.3
C.2
D.1
6.小明在日历的某月上圈出五个数,呈十字框形,若它们的和是55,则中间的数是
(
)
A.9
B.10
C.11
D.12
7.小郑的年龄比妈妈小28岁,今年妈妈的年龄正好是小郑的5倍.小郑今年的年龄是
(
)
A.7岁
B.8岁
C.9岁
D.10岁
8.已知面包店的面包一个15元,小明去此
( http: / / www.21cnjy.com )店买面包,结账时店员告诉小明:“如果你再多买一个面包就可以打九折,价钱会比现在便宜45元.”小明说:“我买这些就好了,谢谢.”根据两人的对话,判断结账时小明买的面包个数是
(
)
A.38
B.39
C.40
D.41
二、填空题
(每题2分,共20分)
9.若3x-5=0,则5x-3=
.
10.当m=
时,方程2x+m=x+l的解为x=-4.
11.若4x2m-1
y
n与-xy2是同类项,则m+n=
.
12.当y=
时,代数式2(3y+4)的值比5
(2y-7)
的值大3.
13.在如图所示的运算程序中,若输出的数y=7,则输入的数x=
.
( http: / / www.21cnjy.com )
14.湖园中学学生志愿服务小组在“三月学雷
( http: / / www.21cnjy.com )锋”活动中,购买了一批牛奶到敬老院慰问老人.如果送给每位老人2盒牛奶,那么剩下16盒;如果送给每位老人3盒牛奶,那么正好送完.设敬老院有x位老人,依题意可列方程为
.
15.甲种电影票每张20元,乙种电影票每张
( http: / / www.21cnjy.com )15元,若购买甲、乙两种电影票共40张,恰好用去700元,则甲种电影票买了
张.
16.某市为提倡节约用水,
( http: / / www.21cnjy.com )采取分段收费.若每户每月用水不超过20
m3,则每立方米收费2元;若用水超过20
m3,则超过部分每立方米加收1元.若小明家5月份交水费64元,则他家该月用水
m3.
17.图1是边长为30
cm的正方形纸
( http: / / www.21cnjy.com )板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知该长方体的宽是高的2倍,则它的体积是
cm3.
( http: / / www.21cnjy.com )
18.某公路一侧原有路灯106盏,
( http: / / www.21cnjy.com )相邻两盏灯的距离为36
m,为节约用电,现计划全部更换为新型节能灯,且相邻两盏灯的距离变为54
m,则需更换新型节能灯
盏.
三、解答题
(共64分)
19.(本题8分)
解下列方程:
(1)
5-=x;
(2)
(x-1)=(2x-3);
(3)
+x=;
(4)
(2x-5)=(
x-3)-.
20.(本题5分)
设a:b,c,d为有理数,现规定一种新的运算:=ad-bc,求满足等式=1的x的值.
21.(本题5分)
当m为何值时,关于x的方程5m+3x=1+x的解比关于x的方程2x+m=3m的解大2
22.(本题5分)
如果代数式的值比的值多1,求a-2的值.
23.(本题5分)
若关于x的方程=2+无论k为何值,方程的解总是x=1,求a,b的值.
24.(本题6分)
把一些图书分给某班学生阅读,若每人分3本,则剩余20本;若每人分4本,则还缺25本.这个班有多少名学生
25.(本题8分)
某一天,一蔬菜
( http: / / www.21cnjy.com )经营户用114元从蔬菜批发市场购进黄瓜和土豆共40
kg到菜市场去卖.黄瓜和土豆这一天的批发价和零售价
(单位:元/kg)如下表所示:
( http: / / www.21cnjy.com )
(1)
他当天购进了黄瓜和土豆各多少千克
(2)
如果黄瓜和土豆全部卖完,他能赚多少钱
26.(本题8分)
李华早上骑自行车上学,中
( http: / / www.21cnjy.com )途因道路施工推车步行了一段路,到学校共用时15
min,如果他骑自行车的平均速度是每分钟250
m,推车步行的平均速度是每分钟80
m,他家离学校的路程是2900
m,求他推车步行的时间.
27.(本题12分)
某景
( http: / / www.21cnjy.com )区内的环形路是边长为800
m的正方形ABCD,如图1和图2所示.现有1号、2号两游览车分别从出口A和景点C同时出发,1号车逆时针、2号车逆时针沿环形路连续循环行驶,供游客随时免费乘车
(上、下车的时间忽略不计),两车速度均为200
m/min.
( http: / / www.21cnjy.com )
[探究]设行驶时间为t
min.
(1)
当0≤t≤8时,
( http: / / www.21cnjy.com )分别用含t的代数式表示1号车、2号车在左半环线离出口A的路程y1,y2
(m),并求出当两车相距的路程是400
m时t的值;
(2)
求当t为何值时,1号车第三次恰好经过景点C,并直接写出这一段时间内它与2号车相遇过的次数.
[发现]
如图2,游客甲在BC上的一点K
(不与点B,C重合)
处候车,准备乘车到出口A.
设CK=x
m.
情况一:若他刚好错过2号车,便搭乘即将到来的1号车;
情况二:若他刚好错过1号车,便搭乘即将到来的2号车.
比较哪种情况用时较多.(含候车时间)
参考答案
一、选择题
1.C
2.B
3.D
4.D
5.B
6.C
7.A
8.B
二、填空题
9.
10.5
11.3
12.10
13.27或28
14.2x+16=3x
15.20
16.28
17.1000
18.71
三、解答题
19.(1)
x=4
(2)
x=-2
(3)
x=
(4)
x=2
20.由题意得-×2=1,则x=-10
21.方程5m+3x=1+x的解是x=,方程2x+m=3m的解是x=m.由题意可知-m=2,解得m=-,即当m=-时,关于x的方程5m+3x=1+x的解比关于x的方程2x+m=3m的解大2
22.由题意得-=1,解得a=5,则a-2的值为3
23.方程两边同时乘以6得4kx+2a=12+x-bk,即(4k-1)
x+2a+bk-12=0
①.因为无论k为何值时,它的解总是1,所以把x=1代入①,得4k-1+2a+bk-12=k(4+b)-13+2a=0,所以4+b=0,-13+2a=0,即b=-4,a=
24.设这个班有x名学生,根据题意得3x+20=4x-25,解得x=45.答:这个班共有45名学生
25.(1)
设购进黄瓜x
kg,则购
( http: / / www.21cnjy.com )进土豆(40-x)
kg,根据题意得2.4x+3(40-x)=114,解得x=10,则40-x=30.答:他购进黄瓜10
kg,购进土豆30
kg
(2)
他能赚10×(4-2.4)+30×(5-3)=76
(元)
26.设他推车步行了x
min,依题意得80x+250(15-x)=2900,解得x=5.答:他推车步行了5
min
27.(1)
y1=200t(0≤t≤8)
y2=1600-200t(0≤t≤8)
当两车相距路程为400
m时,应分两种情况:①当未相遇前,两车相距路程为400
m,则有200t+200t+400=2×800,解得t=3.即当t=3时,两车相距的路程为400
m.
②当相遇之后,两车相距路程为400
m,则有200t+200t=2×800+400,解得t=5.即当t=5时,两车相距的路程为400
m综上所得,当t=3或5时,两车相距的路程为400
m
(2)
当1号车第三次恰好经过景点C时,它已经从A点开始绕正方形2圈半,则可知2×800×4+800×2=200t,解得t=40.即t=40时,1号车第三次恰好经过景点C,且这段时间内它与2号车相遇了5次.[发现]情况一:若他刚好错过2号车,便搭乘即将到来的1号车时,从开始等车到到达出口A,所用时间为
(+)
min,即(16-)
min;情况二:若他刚好错过1号车,便搭乘即将到来的2号车时,从开始等车到到达出口A,所用时间为
(+)
min.即(16+)
min因为16-<16+(
x>0),所以情况二用时较多
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
