八年级上册数学第五章平面直角坐标系复习练习(含答案)
文档属性
| 名称 | 八年级上册数学第五章平面直角坐标系复习练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 112.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-05 00:00:00 | ||
图片预览

文档简介
第五章《平面直角坐标系》复习练习
(满分:100分
时间:60分钟)
一、选择题(每题3分,共24分)
1.下列坐标在第二象限的是
(
)
A.(2,3)
B.(-2,3)
C.(-2,-3)
D.(2,-3)
2.如图所示是我市几个旅游景点的大致位置示意图,如果用(0,0)表示新宁良山的位置,用(1,5)表示隆回花瑶的位置,那么城市南山的位置可以表示为
(
)
A.(2,1)
B.(0,1)
C.(-2,-1)
D.(-2,1)
3.在平面直角坐标系xOy中,若点A的坐标为(-3,3),点B的坐标为(2,0),则△ABO的面积为
(
)
A.15
B.7.5
C.6
D.3
4.如图,△ABC在平面直角坐标系中第二象限内,顶点A的坐标是(-2,3).若先把△ABC向右平移4个单位得到△A1B1C1,再作△A1B1C1关于x轴的对称图形△A2B2C2,则顶点A2的坐标是
(
)
A.(-3,2)
B.(2,-3)
C.(1,-2)
D.(3,-1)
5.一天晚饭后,小明陪妈妈从家里出去散步,上图描述了他们散步过程中离家的距离s(m)与散步时间t(min)之间的函数关系,下面的描述符合他们散步情景的是
(
)
A.从家出发,到了一家书店,看了一会书就回家了
B.从家出发,到了一家书店,看了一会书,继续向前走了一段,然后回家了
C.从家出发,一直散步(没有停留),然后回家了
D.从家出发,散了一会儿步,到了一家书店,看了一会儿书,继续向前走了一段,18分钟后开始返回
6.在物理实验课上,小明用弹簧秤将铁块悬于盛有水的水槽中,然后匀速向上提起(不考虑水的阻力),直到铁块完全露出水面一定高度.下图能反映弹簧秤的度数y(N)与铁块被提起的高度x(
cm)之间关系的大致图像是
(
)
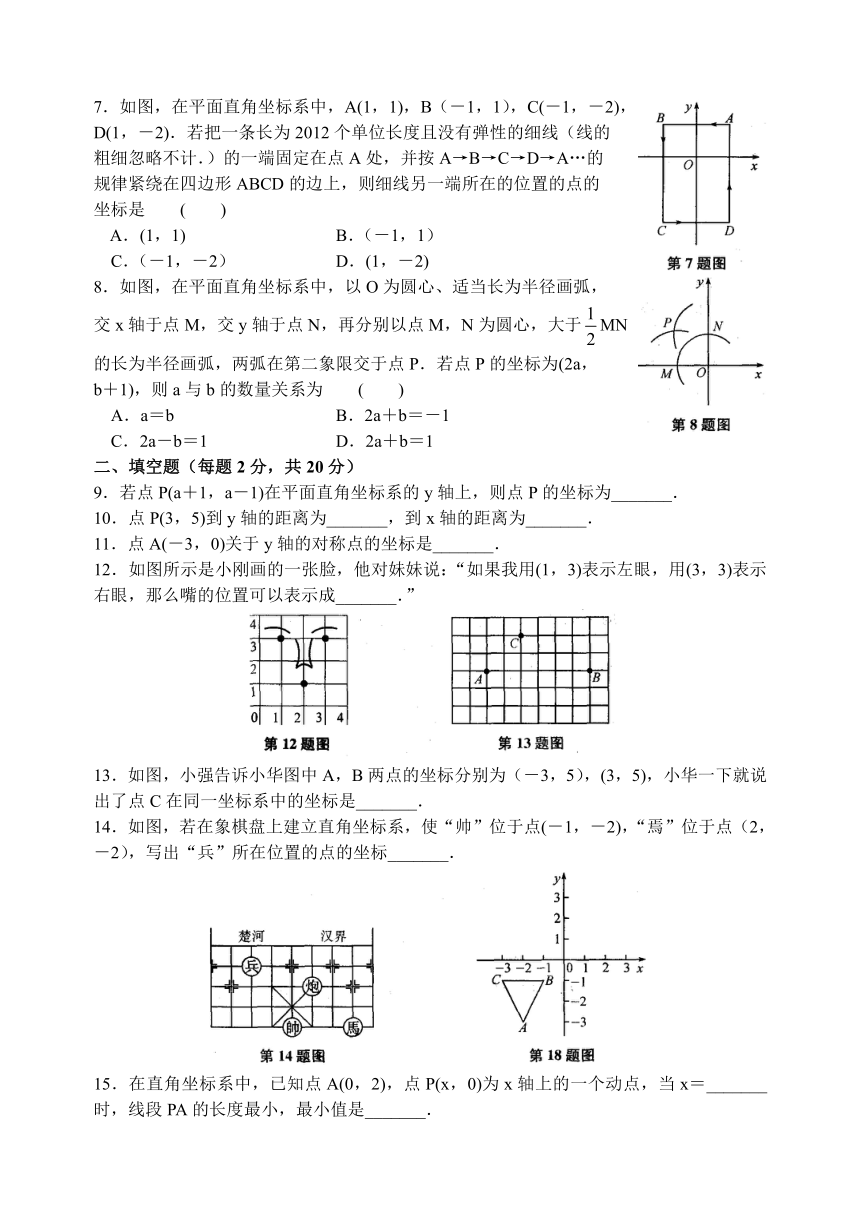
7.如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),
D(1,-2).若把一条长为2012个单位长度且没有弹性的细线(线的
粗细忽略不计.)的一端固定在点A处,并按A→B→C→D→A…的
规律紧绕在四边形ABCD的边上,则细线另一端所在的位置的点的
坐标是
(
)
A.(1,1)
B.(-1,1)
C.(-1,-2)
D.(1,-2)
8.如图,在平面直角坐标系中,以O为圆心、适当长为半径画弧,
交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于MN
的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,
b+1),则a与b的数量关系为
(
)
A.a=b
B.2a+b=-1
C.2a-b=1
D.2a+b=1
二、填空题(每题2分,共20分)
9.若点P(a+1,a-1)在平面直角坐标系的y轴上,则点P的坐标为_______.
10.点P(3,5)到y轴的距离为_______,到x轴的距离为_______.
11.点A(-3,0)关于y轴的对称点的坐标是_______.
12.如图所示是小刚画的一张脸,他对妹妹说:“如果我用(1,3)表示左眼,用(3,3)表示右眼,那么嘴的位置可以表示成_______.”
13.如图,小强告诉小华图中A,B两点的坐标分别为(-3,5),(3,5),小华一下就说出了点C在同一坐标系中的坐标是_______.
14.如图,若在象棋盘上建立直角坐标系,使“帅”位于点(-1,-2),“焉”位于点(2,-2),写出“兵”所在位置的点的坐标_______.
15.在直角坐标系中,已知点A(0,2),点P(x,0)为x轴上的一个动点,当x=_______时,线段PA的长度最小,最小值是_______.
16.在平面直角坐标系中,已知点A(-,0),B(,0),点C在坐标轴上,且AC+BC=6,写出满足条件的所有点C的坐标_______.
17.在平面直角坐标系中,O为坐标原点,点A的坐标为(1,),M为坐标轴上一点,若要使△MOA为等腰三角形,则满足条件的点M的个数为_______.
18.在平面直角坐标系中,规定把一个三角形先沿着x轴翻折,再向右平移2个单位长度称为1次变换.如图,已知等边三角形ABC的顶点B,C的坐标分别是(-1,-1),(-3,-1),若把△ABC经过连续9次这样的变换得到△A'B'C',则点A的对应点A'的坐标是_______.
三、解答题(共56分)
19.(本题6分)如图,点A用(3,1)表示,点B用(8,5)表示,若用(3,1)
→(3,3)
→(5,3)
→(5,4)
→(8,4)
→(8,5)表示由点A到点B的一种走法,并规定从点A到点B只能向上或向右走,试用上述表示方法写出另外两种走法,并判断这几种走法的路程是否相等.
20.(本题6分)如图所示是某公园的景区示意图.
(1)试以游乐园D的坐标(2,-2)、牡丹园E的坐标为(3,3)建立平面直角坐标系,在图中画出来;
(2)分别写出图中其他各景点的坐标.
21.(本题5分)已知点O(0,0),A(3,0),点B在y轴上,且△OAB的面积是6,求点B的坐标.
22.(本题6分)如图,在△OAB中,已知A(2,4),B(6,2),求△OAB的面积.
23.(本题8分)如图,在△ABC中,三个顶点的坐标分别为A(-5,0),B(4,0),C(2,5),将△ABC沿x轴正方向平移2个单位长度,再沿y轴负方向平移1个单位长度得到△EFG.
(1)写出△EFG的三个顶点的坐标;
(2)求△EFG的面积.
24.(本题9分)阅读下面一段文字,然后回答问题.
已知在平面内有两点P1(x1,y1),P2(x2,y2),两点间的距离P1P2=.当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可简化为或.
(1)已知A(2,4),B(-3,-8),试求A,B两点间的距离;
(2)已知A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为-1,试求A,B两点间的距离;
(3)已知一个三角形各顶点的坐标为A0,6),B(-3,2),C(3,2),你能判定此三角形的形状吗?说明理由.
25.(本题12分)在平面直角坐标系中,横坐标、纵坐标都为整数的点叫做整点.设坐标轴的单位长度为1cm,整点P从原点O出发,速度为1cm/s,且整点P只向右或向上运动,则运动1s后它可以到达(0,1),(1,0)两个整点;运劫2s后可以到达(2,0),(1,1).(0,2)三个整点;运动3s后可以到达(3,0),(2,1),(1,2),0,3)四个整点;……
请探索并回答下列问题:
(1)当整点P从点O出发4s后可以到达的整点共有几个?
(2)在直角坐标系中描出:整点P从点O出发8s后所能到
达的整点,并观察这些整点,说出它们在位置上有什么特点;
(3)当整点P从点O出发多少秒后可到达整点(13,5)的位置?
参考答案
一、选择题
1.B
2.C
3.D
4.B
5.D
6.C
7.B
8.B
二、填空题
9.(0,-2)
10.3
5
11.
(3,0)
12.
(2,1)
13.(-1,7)
14.(-3,1)
15.0
2
16.(0,2),(0,22),(-3,0),(3,0)
17.6
18.
(16,3)
三、解答题
19.路程相等
答案不唯一,走法一:(3,1)→(6,1)
→(6,2)
→(7,2)
→(8,2)
→(8,5);走法二:(3,1)
→(3,2)
→(3,5)
→
(4,5)
→(7,5)
→(8,5);等等
20.(1)略
(2)A (0,4)
B(-3,2) C(-2,-1)
21.点B的坐标为(0,4)或(0,-4)
22.10
23.(1)E(-3,-1),F(6,-1),G(4,4)
(2)
24.(1)13
(2)6
(3)等腰三角形
25.(1)共5个
(2)共有9个点,它们在同一直线上
(3)18s
PAGE
(满分:100分
时间:60分钟)
一、选择题(每题3分,共24分)
1.下列坐标在第二象限的是
(
)
A.(2,3)
B.(-2,3)
C.(-2,-3)
D.(2,-3)
2.如图所示是我市几个旅游景点的大致位置示意图,如果用(0,0)表示新宁良山的位置,用(1,5)表示隆回花瑶的位置,那么城市南山的位置可以表示为
(
)
A.(2,1)
B.(0,1)
C.(-2,-1)
D.(-2,1)
3.在平面直角坐标系xOy中,若点A的坐标为(-3,3),点B的坐标为(2,0),则△ABO的面积为
(
)
A.15
B.7.5
C.6
D.3
4.如图,△ABC在平面直角坐标系中第二象限内,顶点A的坐标是(-2,3).若先把△ABC向右平移4个单位得到△A1B1C1,再作△A1B1C1关于x轴的对称图形△A2B2C2,则顶点A2的坐标是
(
)
A.(-3,2)
B.(2,-3)
C.(1,-2)
D.(3,-1)
5.一天晚饭后,小明陪妈妈从家里出去散步,上图描述了他们散步过程中离家的距离s(m)与散步时间t(min)之间的函数关系,下面的描述符合他们散步情景的是
(
)
A.从家出发,到了一家书店,看了一会书就回家了
B.从家出发,到了一家书店,看了一会书,继续向前走了一段,然后回家了
C.从家出发,一直散步(没有停留),然后回家了
D.从家出发,散了一会儿步,到了一家书店,看了一会儿书,继续向前走了一段,18分钟后开始返回
6.在物理实验课上,小明用弹簧秤将铁块悬于盛有水的水槽中,然后匀速向上提起(不考虑水的阻力),直到铁块完全露出水面一定高度.下图能反映弹簧秤的度数y(N)与铁块被提起的高度x(
cm)之间关系的大致图像是
(
)
7.如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),
D(1,-2).若把一条长为2012个单位长度且没有弹性的细线(线的
粗细忽略不计.)的一端固定在点A处,并按A→B→C→D→A…的
规律紧绕在四边形ABCD的边上,则细线另一端所在的位置的点的
坐标是
(
)
A.(1,1)
B.(-1,1)
C.(-1,-2)
D.(1,-2)
8.如图,在平面直角坐标系中,以O为圆心、适当长为半径画弧,
交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于MN
的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,
b+1),则a与b的数量关系为
(
)
A.a=b
B.2a+b=-1
C.2a-b=1
D.2a+b=1
二、填空题(每题2分,共20分)
9.若点P(a+1,a-1)在平面直角坐标系的y轴上,则点P的坐标为_______.
10.点P(3,5)到y轴的距离为_______,到x轴的距离为_______.
11.点A(-3,0)关于y轴的对称点的坐标是_______.
12.如图所示是小刚画的一张脸,他对妹妹说:“如果我用(1,3)表示左眼,用(3,3)表示右眼,那么嘴的位置可以表示成_______.”
13.如图,小强告诉小华图中A,B两点的坐标分别为(-3,5),(3,5),小华一下就说出了点C在同一坐标系中的坐标是_______.
14.如图,若在象棋盘上建立直角坐标系,使“帅”位于点(-1,-2),“焉”位于点(2,-2),写出“兵”所在位置的点的坐标_______.
15.在直角坐标系中,已知点A(0,2),点P(x,0)为x轴上的一个动点,当x=_______时,线段PA的长度最小,最小值是_______.
16.在平面直角坐标系中,已知点A(-,0),B(,0),点C在坐标轴上,且AC+BC=6,写出满足条件的所有点C的坐标_______.
17.在平面直角坐标系中,O为坐标原点,点A的坐标为(1,),M为坐标轴上一点,若要使△MOA为等腰三角形,则满足条件的点M的个数为_______.
18.在平面直角坐标系中,规定把一个三角形先沿着x轴翻折,再向右平移2个单位长度称为1次变换.如图,已知等边三角形ABC的顶点B,C的坐标分别是(-1,-1),(-3,-1),若把△ABC经过连续9次这样的变换得到△A'B'C',则点A的对应点A'的坐标是_______.
三、解答题(共56分)
19.(本题6分)如图,点A用(3,1)表示,点B用(8,5)表示,若用(3,1)
→(3,3)
→(5,3)
→(5,4)
→(8,4)
→(8,5)表示由点A到点B的一种走法,并规定从点A到点B只能向上或向右走,试用上述表示方法写出另外两种走法,并判断这几种走法的路程是否相等.
20.(本题6分)如图所示是某公园的景区示意图.
(1)试以游乐园D的坐标(2,-2)、牡丹园E的坐标为(3,3)建立平面直角坐标系,在图中画出来;
(2)分别写出图中其他各景点的坐标.
21.(本题5分)已知点O(0,0),A(3,0),点B在y轴上,且△OAB的面积是6,求点B的坐标.
22.(本题6分)如图,在△OAB中,已知A(2,4),B(6,2),求△OAB的面积.
23.(本题8分)如图,在△ABC中,三个顶点的坐标分别为A(-5,0),B(4,0),C(2,5),将△ABC沿x轴正方向平移2个单位长度,再沿y轴负方向平移1个单位长度得到△EFG.
(1)写出△EFG的三个顶点的坐标;
(2)求△EFG的面积.
24.(本题9分)阅读下面一段文字,然后回答问题.
已知在平面内有两点P1(x1,y1),P2(x2,y2),两点间的距离P1P2=.当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可简化为或.
(1)已知A(2,4),B(-3,-8),试求A,B两点间的距离;
(2)已知A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为-1,试求A,B两点间的距离;
(3)已知一个三角形各顶点的坐标为A0,6),B(-3,2),C(3,2),你能判定此三角形的形状吗?说明理由.
25.(本题12分)在平面直角坐标系中,横坐标、纵坐标都为整数的点叫做整点.设坐标轴的单位长度为1cm,整点P从原点O出发,速度为1cm/s,且整点P只向右或向上运动,则运动1s后它可以到达(0,1),(1,0)两个整点;运劫2s后可以到达(2,0),(1,1).(0,2)三个整点;运动3s后可以到达(3,0),(2,1),(1,2),0,3)四个整点;……
请探索并回答下列问题:
(1)当整点P从点O出发4s后可以到达的整点共有几个?
(2)在直角坐标系中描出:整点P从点O出发8s后所能到
达的整点,并观察这些整点,说出它们在位置上有什么特点;
(3)当整点P从点O出发多少秒后可到达整点(13,5)的位置?
参考答案
一、选择题
1.B
2.C
3.D
4.B
5.D
6.C
7.B
8.B
二、填空题
9.(0,-2)
10.3
5
11.
(3,0)
12.
(2,1)
13.(-1,7)
14.(-3,1)
15.0
2
16.(0,2),(0,22),(-3,0),(3,0)
17.6
18.
(16,3)
三、解答题
19.路程相等
答案不唯一,走法一:(3,1)→(6,1)
→(6,2)
→(7,2)
→(8,2)
→(8,5);走法二:(3,1)
→(3,2)
→(3,5)
→
(4,5)
→(7,5)
→(8,5);等等
20.(1)略
(2)A (0,4)
B(-3,2) C(-2,-1)
21.点B的坐标为(0,4)或(0,-4)
22.10
23.(1)E(-3,-1),F(6,-1),G(4,4)
(2)
24.(1)13
(2)6
(3)等腰三角形
25.(1)共5个
(2)共有9个点,它们在同一直线上
(3)18s
PAGE
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
