12.2一次函数第4课时分段函数导学案(无答案)
文档属性
| 名称 | 12.2一次函数第4课时分段函数导学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 22.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-06 00:00:00 | ||
图片预览

文档简介
第4课时
分段函数
一、预习热身:
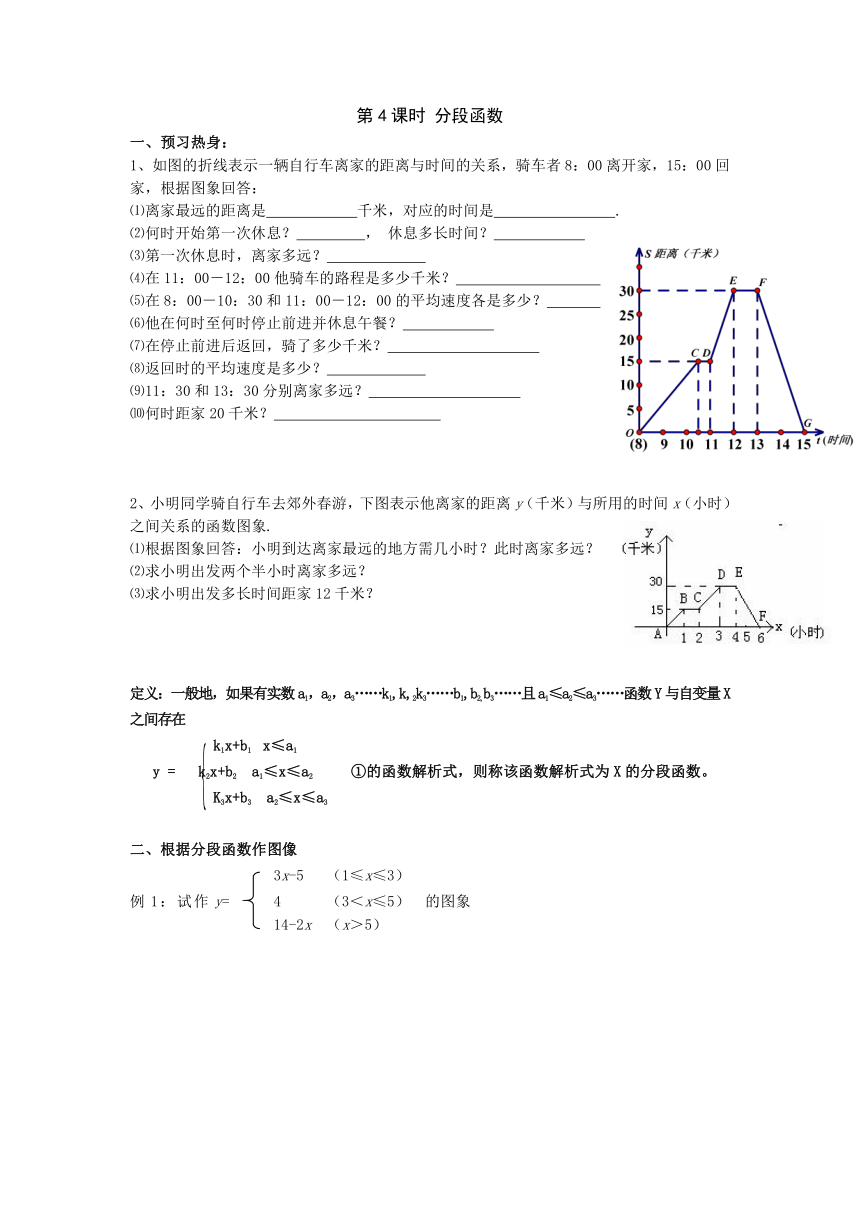
1、如图的折线表示一辆自行车离家的距离与时间的关系,骑车者8:00离开家,15:00回家,根据图象回答:
⑴离家最远的距离是 千米,对应的时间是 .
⑵何时开始第一次休息?
,
休息多长时间?
⑶第一次休息时,离家多远?
⑷在11:00-12:00他骑车的路程是多少千米?
⑸在8:00-10:30和11:00-12:00的平均速度各是多少?
⑹他在何时至何时停止前进并休息午餐?
⑺在停止前进后返回,骑了多少千米?
⑻返回时的平均速度是多少?
⑼11:30和13:30分别离家多远?
⑽何时距家20千米?
2、小明同学骑自行车去郊外春游,下图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.
⑴根据图象回答:小明到达离家最远的地方需几小时?此时离家多远?
⑵求小明出发两个半小时离家多远?
⑶求小明出发多长时间距家12千米?
定义:一般地,如果有实数a1,a2,a3……k1,k,2k3……b1,b2,b3……且a1≤a2≤a3……函数Y与自变量X之间存在
k1x+b1
x≤a1
y
=
k2x+b2
a1≤x≤a2
①的函数解析式,则称该函数解析式为X的分段函数。
K3x+b3
a2≤x≤a3
二、根据分段函数作图像
3x-5
(1≤x≤3)
例1:试作y=
4
(3<x≤5)
的图象
14-2x
(x>5)
例2:某城市出租车收费标准如下,3千米以内(含3千米)收8元,超过3千米的部分每千米收费1.4元。求出应收车费Y(元)与出租车行驶路程X千米之间的函数关系式。
注意:在作分段函数图像时,一般先求出每一段图像的端点坐标,然后在坐标系中描出点,分段连线即可,对于具有特殊意义的图像,还需根据其意义的具体要求确定图像。
练习:
3X-5
0≤X≤3
1:试作y=
4
3<X≤5
的图像
14-2X
X>5
2:作Y=|X-3|+|X+1|+|X+3|的图像
分段函数
一、预习热身:
1、如图的折线表示一辆自行车离家的距离与时间的关系,骑车者8:00离开家,15:00回家,根据图象回答:
⑴离家最远的距离是 千米,对应的时间是 .
⑵何时开始第一次休息?
,
休息多长时间?
⑶第一次休息时,离家多远?
⑷在11:00-12:00他骑车的路程是多少千米?
⑸在8:00-10:30和11:00-12:00的平均速度各是多少?
⑹他在何时至何时停止前进并休息午餐?
⑺在停止前进后返回,骑了多少千米?
⑻返回时的平均速度是多少?
⑼11:30和13:30分别离家多远?
⑽何时距家20千米?
2、小明同学骑自行车去郊外春游,下图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.
⑴根据图象回答:小明到达离家最远的地方需几小时?此时离家多远?
⑵求小明出发两个半小时离家多远?
⑶求小明出发多长时间距家12千米?
定义:一般地,如果有实数a1,a2,a3……k1,k,2k3……b1,b2,b3……且a1≤a2≤a3……函数Y与自变量X之间存在
k1x+b1
x≤a1
y
=
k2x+b2
a1≤x≤a2
①的函数解析式,则称该函数解析式为X的分段函数。
K3x+b3
a2≤x≤a3
二、根据分段函数作图像
3x-5
(1≤x≤3)
例1:试作y=
4
(3<x≤5)
的图象
14-2x
(x>5)
例2:某城市出租车收费标准如下,3千米以内(含3千米)收8元,超过3千米的部分每千米收费1.4元。求出应收车费Y(元)与出租车行驶路程X千米之间的函数关系式。
注意:在作分段函数图像时,一般先求出每一段图像的端点坐标,然后在坐标系中描出点,分段连线即可,对于具有特殊意义的图像,还需根据其意义的具体要求确定图像。
练习:
3X-5
0≤X≤3
1:试作y=
4
3<X≤5
的图像
14-2X
X>5
2:作Y=|X-3|+|X+1|+|X+3|的图像
