第二章 平面向量单元综合检测题二(带解析)
文档属性
| 名称 | 第二章 平面向量单元综合检测题二(带解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 661.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-07 00:00:00 | ||
图片预览




文档简介
第二章 平面向量单元综合检测题二(带解析)
一、选择题
1.已知,,,则向量在向量方向上的投影是( )
A.-4 B.4 C.-2 D.2
2.已知两点A(4,1),B(7,-3),则与向量同向的单位向量是( )
A.±(,-) B.(-,) C.(,-) D.(,-
3.已知向量与反向,下列等式中成立的是( )
A.=|| B.||=|| C.||+||=|| D.||+||=||
4.已知向量,,P是线段AB的中点,则P点的坐标是( )
A.(2,-4) B.(3,1) C.(-2,4) D.(6,2)
5.若A、B、C、D是平面内任意四点,给出下列式子:①+=+;②+=+;③-=+.其中正确的有( ) 21*cnjy*com
A.0个 B.1个 C.2个 D.3个
6.已知向量=(-2,-1), =(λ,1),若与的夹角为钝角,则实数λ的取值范围是 ( )
A. B.
C. D.
7.已知、分别是与x轴、y轴方向相同的单位向量,且=-3+6,=-6+4,=--6,则一定共线的三点是( )21cnjy.com
A.A,B,C B.A,B,D C.A,C,D D.B,C,D
8.若A(2,-1),B(-1,3),则的坐标是( )
A.(1,2) B.(-1,-2) C.(-3,4) D.(3,-4)
9.在△ABC中,若?+2=0,则△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形
10.,向量与的位置关系为( )
A.垂直 B.平行 C.夹角为 D.不平行也不垂直
11.如图,平面内的两条相交直线OP1和OP2将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ(不包括边界).若,且点P落在第Ⅲ部分,则实数a、b满足( )
A.a>0,b>0 B.a>0,b<0 C.a<0,b>0 D.a<0,b<0【来源:21·世纪·教育·网】
二、填空题
12.在△ABC中,a2+b2=c2+ab,且sinAsinB=,则三角形为 ??? 三角形.
13.△ABC是边长为1的正三角形,点O是平面上任意一点,则=??? .
14.向量,若记非零向量与非零向量的夹角为θ,则函数的单调递减区间为??? .【来源:21cnj*y.co*m】
15.定义平面向量之间的一种运算“?”如下,对任意的=(m,n),=(p,q),令?=mq-np,给出下面五个判断: ①若与共线,则?=0; ②若与垂直,则?=0; ③?=?; ④对任意的λ∈R,有; ⑤(?)2+2=||2||2 其中正确的有??? (请把正确的序号都写出).【出处:21教育名师】
三、解答题
16.已知.
(1)求及;
(2)若与垂直,求实数的值.
17.设向量??且其中是的内角.
(Ⅰ)求的取值范围;
(Ⅱ)试确定的取值范围.
18.已知向量. (1)求的坐标表示; (2)若与共线,求实数t.
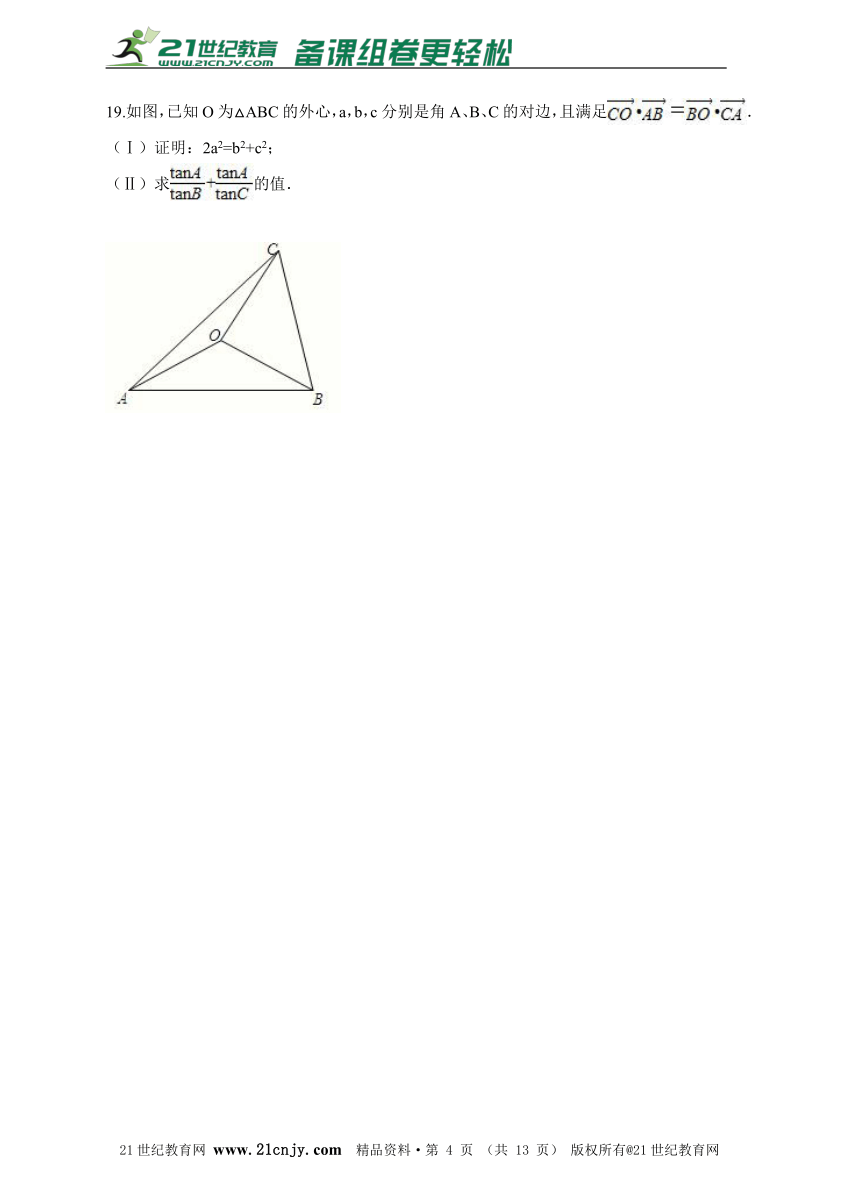
19.如图,已知O为△ABC的外心,a,b,c分别是角A、B、C的对边,且满足. (Ⅰ)证明:2a2=b2+c2;? (Ⅱ)求的值.21世纪教育网版权所有
20.已知,, (1)求的坐标; (2)当k为何值时,与垂直?. (3)设向量与的夹角为θ,求cos2θ的值.21教育网
21.三角形ABC中,三内角∠A,∠B,∠C的对边分别为a,b,c,c=10,且==. (1)求证:三角形ABC是直角三角形; (2)过AB中点E作直线MN与射线CA,CB分别交于M,N,求|ME|?|NE|的最小值,并求出此时直线MN的方程.21·cn·jy·com
参考答案及解析
1.A 【解析】根据投影的定义,
4.B 【解析】由线段的中点公式可得=()=(3,1),故P点的坐标是(3,1), 5.C 【解析】①式的等价式是,左边=,右边=,不一定相等; ②式的等价式是,即成立; ③式的等价式是=成立. 综上可知正确的是②③. 6.Awww.21-cn-jy.com
【解析】由题意可得,若与夹角为钝角,
则×且,
故
所以实数的取值范围为
7.C 【解析】由题意得? ?? ∴=(2,-4) ∴ 所以△ABC是直角三角形. 10.A 【解析】由于==0 所以向量与的位置关系是垂直. 11.B 【解析】∵=a+b, 由于点P落在第Ⅲ部分, 则根据实数与向量的积的定义及平行四边形法则知a与方向相同, b与方向相反, ∴a>0,b<0. 12.等边三角形 【解析】由余弦定理,得c2=a2+b2-2abcosC. ∵a2+b2=c2+ab, ∴ab-2abcosC=0. ∴cosC=,∴C=60° ∵sinAsinB=,cos(A+B)=cos(180°-C)=cos120°=-, cos(A+B)=cosAcosB-sinAsinB, ∴cosAcosB= ∴cos(A-B)=cosAcosB+sinAsinB=1. ∵-π<A-B<π,∴A-B=0. ∴A=B=60° ∴△ABC是等边三角形. 13. =0. 又∵≠,≠; ∴⊥; ∴θ=. ∴y=sin(θ-2x)=cos2x; 令2kπ≤2x≤2kπ+π?kπ≤x≤kπ+,k∈Z. 与[0,]取交集得[0,]. 15.①④⑤ 【解析】①若与共线,则由向量共线的坐标表示可得,mq-np=0,而?=mq-np=0,正确; ②若与垂直,则由向量垂直的坐标表示可得,=mp+nq=0,而?=mq-np=0不一定成立,错误; ③由题目定义可得,?=mq-np,?=pn-mq,不一定相等,错误; ④对任意的λ∈R,?=λmq-λnp=λ(mq-np)=λ?正确 (2),,21·世纪*教育网
,,
解得:
17.(Ⅰ)?(Ⅱ)
【解析】因为,
所以,??????????????????????????????
即?
又所以即?????????????????????
(Ⅰ)=?
???
因此的取值范围是??????????????
(Ⅱ)由(Ⅰ)得,所以
设=,则,所以
即?令?则????
故实数t=. 19.(Ⅰ)2a2=b2+c2. (Ⅱ)2 【解析】(Ⅰ)取AB、AC的中点E、F,2·1·c·n·j·y
则
同理; 所以2a2=b2+c2. (k+)?(-3)=10(k-3)-4(2k+2)=2k-38=0, k=19www-2-1-cnjy-com
(3)依题意,cosθ=, ∴cos2θ=2cos2θ-1=- 21.(1)三角形ABC是直角三角形 (2)x+y-7=0 【解析】(1)证明:由正弦定理得,, 则sinAcosA=sinBcosB,即sin2A=sin2B, ∴2A=2B或2A+2B=π,即A=B或A+B=, 又∵,∴A≠B,则A+B=,C=. ∴三角形ABC是直角三角形, (2)解:以C为原点,CA、CB分别为x轴,y轴建系如图:2-1-c-n-j-y
则A(8,0),B(0,6),从而E(4,3). 设∠NMC=θ,则,,. 当2θ=90°,θ=45°时,|EM|?|EN|最小值为24. ∴直线MN的斜率是-1,则直线MN方程为y-3=-(x-4), 即直线MN的方程x+y-7=0.
一、选择题
1.已知,,,则向量在向量方向上的投影是( )
A.-4 B.4 C.-2 D.2
2.已知两点A(4,1),B(7,-3),则与向量同向的单位向量是( )
A.±(,-) B.(-,) C.(,-) D.(,-
3.已知向量与反向,下列等式中成立的是( )
A.=|| B.||=|| C.||+||=|| D.||+||=||
4.已知向量,,P是线段AB的中点,则P点的坐标是( )
A.(2,-4) B.(3,1) C.(-2,4) D.(6,2)
5.若A、B、C、D是平面内任意四点,给出下列式子:①+=+;②+=+;③-=+.其中正确的有( ) 21*cnjy*com
A.0个 B.1个 C.2个 D.3个
6.已知向量=(-2,-1), =(λ,1),若与的夹角为钝角,则实数λ的取值范围是 ( )
A. B.
C. D.
7.已知、分别是与x轴、y轴方向相同的单位向量,且=-3+6,=-6+4,=--6,则一定共线的三点是( )21cnjy.com
A.A,B,C B.A,B,D C.A,C,D D.B,C,D
8.若A(2,-1),B(-1,3),则的坐标是( )
A.(1,2) B.(-1,-2) C.(-3,4) D.(3,-4)
9.在△ABC中,若?+2=0,则△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形
10.,向量与的位置关系为( )
A.垂直 B.平行 C.夹角为 D.不平行也不垂直
11.如图,平面内的两条相交直线OP1和OP2将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ(不包括边界).若,且点P落在第Ⅲ部分,则实数a、b满足( )
A.a>0,b>0 B.a>0,b<0 C.a<0,b>0 D.a<0,b<0【来源:21·世纪·教育·网】
二、填空题
12.在△ABC中,a2+b2=c2+ab,且sinAsinB=,则三角形为 ??? 三角形.
13.△ABC是边长为1的正三角形,点O是平面上任意一点,则=??? .
14.向量,若记非零向量与非零向量的夹角为θ,则函数的单调递减区间为??? .【来源:21cnj*y.co*m】
15.定义平面向量之间的一种运算“?”如下,对任意的=(m,n),=(p,q),令?=mq-np,给出下面五个判断: ①若与共线,则?=0; ②若与垂直,则?=0; ③?=?; ④对任意的λ∈R,有; ⑤(?)2+2=||2||2 其中正确的有??? (请把正确的序号都写出).【出处:21教育名师】
三、解答题
16.已知.
(1)求及;
(2)若与垂直,求实数的值.
17.设向量??且其中是的内角.
(Ⅰ)求的取值范围;
(Ⅱ)试确定的取值范围.
18.已知向量. (1)求的坐标表示; (2)若与共线,求实数t.
19.如图,已知O为△ABC的外心,a,b,c分别是角A、B、C的对边,且满足. (Ⅰ)证明:2a2=b2+c2;? (Ⅱ)求的值.21世纪教育网版权所有
20.已知,, (1)求的坐标; (2)当k为何值时,与垂直?. (3)设向量与的夹角为θ,求cos2θ的值.21教育网
21.三角形ABC中,三内角∠A,∠B,∠C的对边分别为a,b,c,c=10,且==. (1)求证:三角形ABC是直角三角形; (2)过AB中点E作直线MN与射线CA,CB分别交于M,N,求|ME|?|NE|的最小值,并求出此时直线MN的方程.21·cn·jy·com
参考答案及解析
1.A 【解析】根据投影的定义,
4.B 【解析】由线段的中点公式可得=()=(3,1),故P点的坐标是(3,1), 5.C 【解析】①式的等价式是,左边=,右边=,不一定相等; ②式的等价式是,即成立; ③式的等价式是=成立. 综上可知正确的是②③. 6.Awww.21-cn-jy.com
【解析】由题意可得,若与夹角为钝角,
则×且,
故
所以实数的取值范围为
7.C 【解析】由题意得? ?? ∴=(2,-4) ∴ 所以△ABC是直角三角形. 10.A 【解析】由于==0 所以向量与的位置关系是垂直. 11.B 【解析】∵=a+b, 由于点P落在第Ⅲ部分, 则根据实数与向量的积的定义及平行四边形法则知a与方向相同, b与方向相反, ∴a>0,b<0. 12.等边三角形 【解析】由余弦定理,得c2=a2+b2-2abcosC. ∵a2+b2=c2+ab, ∴ab-2abcosC=0. ∴cosC=,∴C=60° ∵sinAsinB=,cos(A+B)=cos(180°-C)=cos120°=-, cos(A+B)=cosAcosB-sinAsinB, ∴cosAcosB= ∴cos(A-B)=cosAcosB+sinAsinB=1. ∵-π<A-B<π,∴A-B=0. ∴A=B=60° ∴△ABC是等边三角形. 13. =0. 又∵≠,≠; ∴⊥; ∴θ=. ∴y=sin(θ-2x)=cos2x; 令2kπ≤2x≤2kπ+π?kπ≤x≤kπ+,k∈Z. 与[0,]取交集得[0,]. 15.①④⑤ 【解析】①若与共线,则由向量共线的坐标表示可得,mq-np=0,而?=mq-np=0,正确; ②若与垂直,则由向量垂直的坐标表示可得,=mp+nq=0,而?=mq-np=0不一定成立,错误; ③由题目定义可得,?=mq-np,?=pn-mq,不一定相等,错误; ④对任意的λ∈R,?=λmq-λnp=λ(mq-np)=λ?正确 (2),,21·世纪*教育网
,,
解得:
17.(Ⅰ)?(Ⅱ)
【解析】因为,
所以,??????????????????????????????
即?
又所以即?????????????????????
(Ⅰ)=?
???
因此的取值范围是??????????????
(Ⅱ)由(Ⅰ)得,所以
设=,则,所以
即?令?则????
故实数t=. 19.(Ⅰ)2a2=b2+c2. (Ⅱ)2 【解析】(Ⅰ)取AB、AC的中点E、F,2·1·c·n·j·y
则
同理; 所以2a2=b2+c2. (k+)?(-3)=10(k-3)-4(2k+2)=2k-38=0, k=19www-2-1-cnjy-com
(3)依题意,cosθ=, ∴cos2θ=2cos2θ-1=- 21.(1)三角形ABC是直角三角形 (2)x+y-7=0 【解析】(1)证明:由正弦定理得,, 则sinAcosA=sinBcosB,即sin2A=sin2B, ∴2A=2B或2A+2B=π,即A=B或A+B=, 又∵,∴A≠B,则A+B=,C=. ∴三角形ABC是直角三角形, (2)解:以C为原点,CA、CB分别为x轴,y轴建系如图:2-1-c-n-j-y
则A(8,0),B(0,6),从而E(4,3). 设∠NMC=θ,则,,. 当2θ=90°,θ=45°时,|EM|?|EN|最小值为24. ∴直线MN的斜率是-1,则直线MN方程为y-3=-(x-4), 即直线MN的方程x+y-7=0.
