第二章 平面向量单元综合检测题三(带解析)
文档属性
| 名称 | 第二章 平面向量单元综合检测题三(带解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 739.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-07 00:00:00 | ||
图片预览



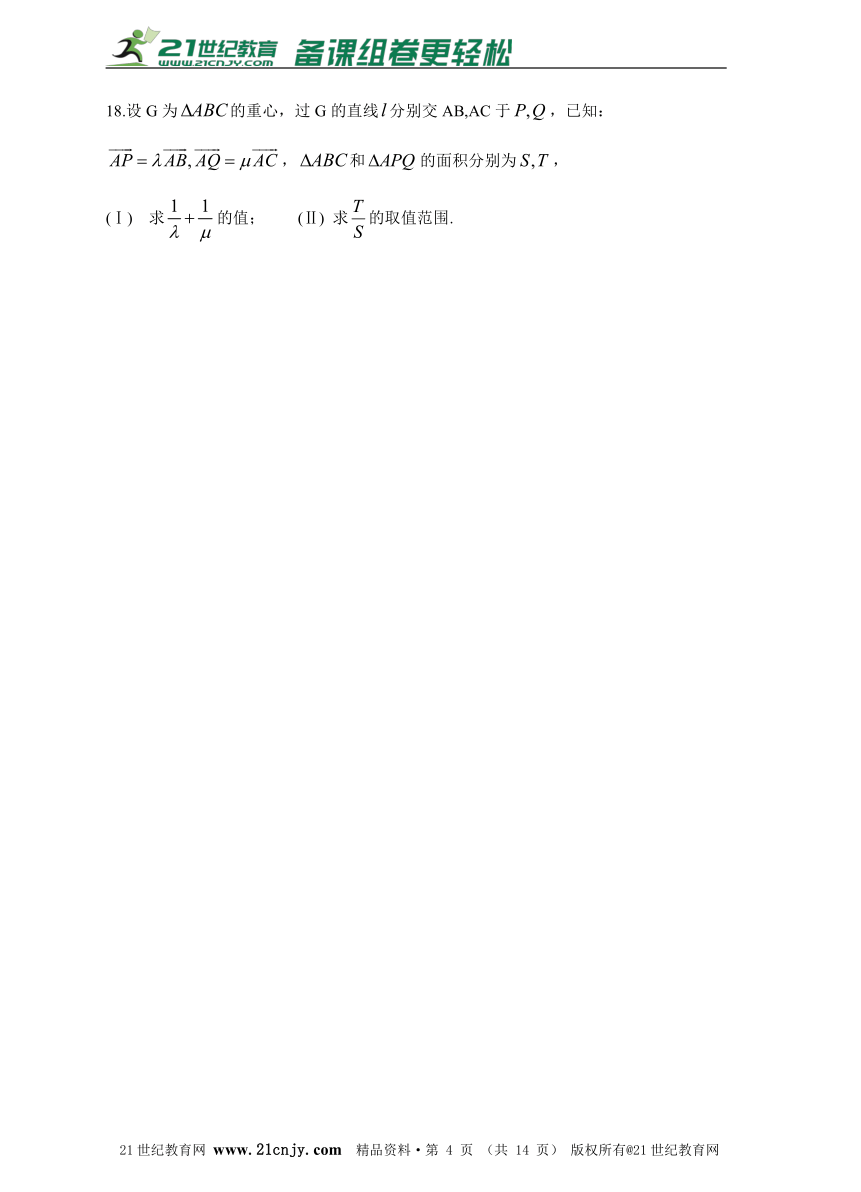

文档简介
第二章 平面向量单元综合检测题三(带解析)
一、选择题
1.已知,,,则等于( )
A. B. C. D.
2.在中,,.若点满足,则(???)
A. B. C. D.
3.已知|a|=1,|b|=6,a·(b-a)=2,则向量a与向量b的夹角是( )
A. B. C. D.
4.在△ABC中,,如果不等式恒成立,则实数t的取值范围是( )
A.[1,+∞) B.
C. D.(-∞,0]∪[1,+∞)
5.若非零向量,满足|+|=||,则( )
A.|2|>|2+| B.|2|<|2+| C.|2|>|+2| D.|2|<|+2|
6.已知,,,则下列关系一定成立的是( )
A.A,B,C三点共线 B.A,C,D三点共线 C.A,B,D三点共线 D.B,C,D三点共线
7.下列说法正确的是( )
A.若∥,∥,则∥ B.若,则2α的终边在第四象限 C.若?,与垂直的单位向量的坐标为 D.若2α是小于180°的角,则α为锐角【来源:21·世纪·教育·网】
8.若AD是△ABC的中线,已知=,,则等于( )
A. B. C. D.
9.已知AM是△ABC的BC边上的中线,若、,则等于( )
A.(-) B.-(-) C.(+) D.-(-)
10.已知向量=(1,2),=(0,1),设=+,=2-,若∥,则实数k的值为( )21·世纪*教育网
A.-1 B.1 C. D.-
11.如图在矩形ABCD中,AB=,BC=4,点E为BC的中点,点F在CD上,若,则的值是( )www-2-1-cnjy-com
A. B. C. D.
二、填空题
12.在△ABC中,a2+b2=c2+ab,且sinAsinB=,则三角形为 ??? 三角形.
13.已知ABCD为平行四边形,A(-1,2),B?(0,0),C(1,7),则D点坐标为??? .
14.已知平面向量满足,且与的夹角为135°,与的夹角为120°,,则=??? .2-1-c-n-j-y
15.已知角α的顶点与直角坐标系原点O重合,始边与x轴的非负半轴重合,终边与单位圆交于点P,且α∈[0,π)设点M的坐标是,求使得函数的恰有两个零点的实数k的取值范围? ?? . 21*cnjy*com
三、解答题
16.如图,平行四边形ABCD中,=a,=b,H、M是AD、DC之中点,F使BF=BC,(1)以a、b为基底表示向量与;(2)若|a|=3,|b|=4,a与b的夹角为,求.
17.设向量,,函数,求f(x)的最大值、最小正周期和单调区间.
18.设G为的重心,过G的直线分别交AB,AC于,已知:,和的面积分别为,
(Ⅰ) 求的值; (Ⅱ) 求的取值范围.
19.已知向量=(sinθ,cosθ-2sinθ),=(1,2). (1)若,求tanθ的值; (2)若,求θ的值.21世纪教育网版权所有
20.在△ABC中,角A、B、C所对的边分别为a、b、c,且. (1)求的值; (2)若b=2,BC边上的中线AD=求c.21教育网
21.已知向量. (1)若点A,B,C能构成三角形,求x,y应满足的条件; (2)若△ABC为等腰直角三角形,且∠B为直角,求x,y的值.21cnjy.com
参考答案及解析
1.D
【解析】
∴ ∵恒成立 ∴恒成立 即3-6t+4t2≥1即4t2-6t+2≥0 解得 5.C 【解析】∵|+2|=|++|≤|+|+||=2||, ∵,是非零向量, ∴必有+≠, ∴上式中等号不成立. ∴|2|>|+2|, 6.B 【解析】,,, 由向量的加法原理知=+=+==2 又两线段过同点C,故三点A,C,D一定共线. 7.B 【解析】当时,由∥,∥,不见得有∥; 由,所以,k∈Z. 所以,k∈Z.则2α的终边在第四象限; ∴=(+). 10.D 【解析】=2-=(2-0,4-1)=(2,3);=+k=(1+k×0,2+k)=(1,k+2), ∵∥,∴=2?k=-. 11.B 【解析】选基向量和,由题意得,=,=4, ∴, ∴==+=, 即cos0=,解得=1, ∵点E为BC的中点,=1, ∴,, ∴=()?() ==5+, 12.等边 解得 ∴D(0,9) 14.21·cn·jy·com
【解析】由已知,可知三个向量首尾相接后,构成一个三角形,且与的夹角为135°,与的夹角为120°,,可以得到三角形的两个内角和一边的长,利用正弦定理,可求出向量对应边的长度. www.21-cn-jy.com
∵ ∴三个向量首尾相接后,构成一个三角形 且与的夹角为135°,与的夹角为120°,, 故所得三角形如下图示: 其中∠C=45°,∠A=60°,AB=2 【解析】)(1)利用平面向量基本定理及三角形法则用基底表示所给向量;(2)利用数量积运算律及定义求出数量积.2·1·c·n·j·y
(1)由H、M、F所在位置有:=b+a,=a-b
(2)∵=
17.单调递增区间是(k∈Z)
单调递减区间是(k∈Z) 【解析】∵向量,, ∴, ∴当2x=+2kπ,k∈Z时,f(x)的最大值是, 函数的最小正周期T===π, ,
三点共线,故存在实数,使,
,消得:,即
或者另一种解法由②式得, ③
将③代入①得.三点共线,
故,即 .
∴tanθ= (2)由|a|=|b| ∴sin2θ+(cosθ-2sinθ)2=5 即1-2sin2θ+4sin2θ=5化简得sin2θ+cos2θ=-1 故有sin(2θ+)=- 又∵θ∈(0,π)∴2θ+∈(,π) ∴2θ+=π或2θ+=π ∴θ=或θ=π 20.(1) (2) 【解析】(1) = = ∴x,y满足的条件为3y-x≠1 (2)∵=(3,1),=(-x-1,-y),若∠B为直角,则AB⊥BC, ∴3(-x-1)-y=0, 又|AB|=|BC|,∴(x+1)2+y2=10, 再由3(-x-1)-y=0,解得或.
一、选择题
1.已知,,,则等于( )
A. B. C. D.
2.在中,,.若点满足,则(???)
A. B. C. D.
3.已知|a|=1,|b|=6,a·(b-a)=2,则向量a与向量b的夹角是( )
A. B. C. D.
4.在△ABC中,,如果不等式恒成立,则实数t的取值范围是( )
A.[1,+∞) B.
C. D.(-∞,0]∪[1,+∞)
5.若非零向量,满足|+|=||,则( )
A.|2|>|2+| B.|2|<|2+| C.|2|>|+2| D.|2|<|+2|
6.已知,,,则下列关系一定成立的是( )
A.A,B,C三点共线 B.A,C,D三点共线 C.A,B,D三点共线 D.B,C,D三点共线
7.下列说法正确的是( )
A.若∥,∥,则∥ B.若,则2α的终边在第四象限 C.若?,与垂直的单位向量的坐标为 D.若2α是小于180°的角,则α为锐角【来源:21·世纪·教育·网】
8.若AD是△ABC的中线,已知=,,则等于( )
A. B. C. D.
9.已知AM是△ABC的BC边上的中线,若、,则等于( )
A.(-) B.-(-) C.(+) D.-(-)
10.已知向量=(1,2),=(0,1),设=+,=2-,若∥,则实数k的值为( )21·世纪*教育网
A.-1 B.1 C. D.-
11.如图在矩形ABCD中,AB=,BC=4,点E为BC的中点,点F在CD上,若,则的值是( )www-2-1-cnjy-com
A. B. C. D.
二、填空题
12.在△ABC中,a2+b2=c2+ab,且sinAsinB=,则三角形为 ??? 三角形.
13.已知ABCD为平行四边形,A(-1,2),B?(0,0),C(1,7),则D点坐标为??? .
14.已知平面向量满足,且与的夹角为135°,与的夹角为120°,,则=??? .2-1-c-n-j-y
15.已知角α的顶点与直角坐标系原点O重合,始边与x轴的非负半轴重合,终边与单位圆交于点P,且α∈[0,π)设点M的坐标是,求使得函数的恰有两个零点的实数k的取值范围? ?? . 21*cnjy*com
三、解答题
16.如图,平行四边形ABCD中,=a,=b,H、M是AD、DC之中点,F使BF=BC,(1)以a、b为基底表示向量与;(2)若|a|=3,|b|=4,a与b的夹角为,求.
17.设向量,,函数,求f(x)的最大值、最小正周期和单调区间.
18.设G为的重心,过G的直线分别交AB,AC于,已知:,和的面积分别为,
(Ⅰ) 求的值; (Ⅱ) 求的取值范围.
19.已知向量=(sinθ,cosθ-2sinθ),=(1,2). (1)若,求tanθ的值; (2)若,求θ的值.21世纪教育网版权所有
20.在△ABC中,角A、B、C所对的边分别为a、b、c,且. (1)求的值; (2)若b=2,BC边上的中线AD=求c.21教育网
21.已知向量. (1)若点A,B,C能构成三角形,求x,y应满足的条件; (2)若△ABC为等腰直角三角形,且∠B为直角,求x,y的值.21cnjy.com
参考答案及解析
1.D
【解析】
∴ ∵恒成立 ∴恒成立 即3-6t+4t2≥1即4t2-6t+2≥0 解得 5.C 【解析】∵|+2|=|++|≤|+|+||=2||, ∵,是非零向量, ∴必有+≠, ∴上式中等号不成立. ∴|2|>|+2|, 6.B 【解析】,,, 由向量的加法原理知=+=+==2 又两线段过同点C,故三点A,C,D一定共线. 7.B 【解析】当时,由∥,∥,不见得有∥; 由,所以,k∈Z. 所以,k∈Z.则2α的终边在第四象限; ∴=(+). 10.D 【解析】=2-=(2-0,4-1)=(2,3);=+k=(1+k×0,2+k)=(1,k+2), ∵∥,∴=2?k=-. 11.B 【解析】选基向量和,由题意得,=,=4, ∴, ∴==+=, 即cos0=,解得=1, ∵点E为BC的中点,=1, ∴,, ∴=()?() ==5+, 12.等边 解得 ∴D(0,9) 14.21·cn·jy·com
【解析】由已知,可知三个向量首尾相接后,构成一个三角形,且与的夹角为135°,与的夹角为120°,,可以得到三角形的两个内角和一边的长,利用正弦定理,可求出向量对应边的长度. www.21-cn-jy.com
∵ ∴三个向量首尾相接后,构成一个三角形 且与的夹角为135°,与的夹角为120°,, 故所得三角形如下图示: 其中∠C=45°,∠A=60°,AB=2 【解析】)(1)利用平面向量基本定理及三角形法则用基底表示所给向量;(2)利用数量积运算律及定义求出数量积.2·1·c·n·j·y
(1)由H、M、F所在位置有:=b+a,=a-b
(2)∵=
17.单调递增区间是(k∈Z)
单调递减区间是(k∈Z) 【解析】∵向量,, ∴, ∴当2x=+2kπ,k∈Z时,f(x)的最大值是, 函数的最小正周期T===π, ,
三点共线,故存在实数,使,
,消得:,即
或者另一种解法由②式得, ③
将③代入①得.三点共线,
故,即 .
∴tanθ= (2)由|a|=|b| ∴sin2θ+(cosθ-2sinθ)2=5 即1-2sin2θ+4sin2θ=5化简得sin2θ+cos2θ=-1 故有sin(2θ+)=- 又∵θ∈(0,π)∴2θ+∈(,π) ∴2θ+=π或2θ+=π ∴θ=或θ=π 20.(1) (2) 【解析】(1) = = ∴x,y满足的条件为3y-x≠1 (2)∵=(3,1),=(-x-1,-y),若∠B为直角,则AB⊥BC, ∴3(-x-1)-y=0, 又|AB|=|BC|,∴(x+1)2+y2=10, 再由3(-x-1)-y=0,解得或.
