3.2简单的三角恒等变换(带解析)
文档属性
| 名称 | 3.2简单的三角恒等变换(带解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 536.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-07 00:00:00 | ||
图片预览

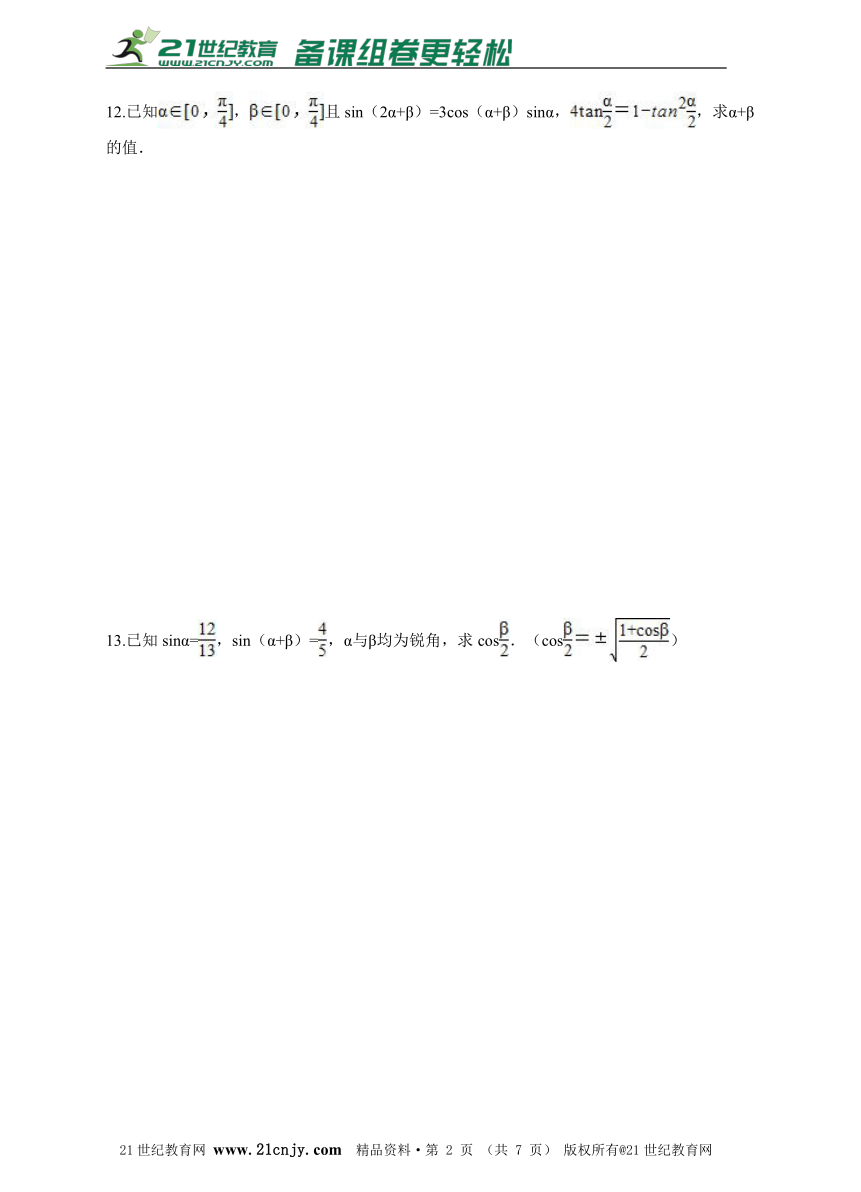

文档简介
3.2简单的三角恒等变换(带解析)
一、选择题
1.已知180°<α<360°,则的值等于( )
A. B. C. D.
2.若2sinx=1+cosx,则的值等于( )
A. B.或不存在 C.2 D.2或
3.已知sinα=,<α<π,则tan的值为( )
A. B.-2 C.2 D.
4.已知的值为( )
A. B. C. D.
5.设的值是( )
A. B. C. D.
6.α,β都是锐角,且,,则sinβ的值是( )
A. B. C. D.
7.在△ABC中,若,则△ABC是( )
A.等边三角形 B.等腰三角形 C.不等边三角形 D.直角三角形
8.已知f(x)=sin(3x+θ)-cos(3x+θ)是奇函数且在区间上是减函数,则θ的一个值是( )21教育网
A. B.π C. D.
二、填空题
9.已知,则tanα的值为?? ? .
10.若的值为??? .
11.已知函数f(x)=(sinx-cosx)sinx,x∈R,则f(x)的最小正周期是??? .
三、解答题
12.已知,且sin(2α+β)=3cos(α+β)sinα,,求α+β的值.
13.已知sinα=,sin(α+β)=,α与β均为锐角,求cos.(cos)
14.已知sin=,cos=-,试确定θ的象限.
15.在△ABC中,角A,B,C的对边分别是a,b,c,已知sinC+cosC=1-sin (1)求sinC的值 (2)若?a2+b2=4(a+b)-8,求边c的值.21世纪教育网版权所有
参考答案及解析
1.B 【解析】∵已知180°<α<360°,∴90°<<180°,故>0. ∴=, 2.B 【解析】∵2sinx=1+cosx, ∴2×2sincos=1+(2cos2-1), ∴+==, ∴sinα= ∴cos2α=1-2sin2α=1-2×()2=, 5.B 【解析】==== 6.C 【解析】α,β都是锐角,∴α+β∈(0,π), ∵∴cosα===, ∵ ∴sin(α+β)=== 【解析】tanα===-, 10. 【解析】∵=cos2(+α)=2-1=2-1 =2×-1=, 11.π 【解析】∵f(x)=sin2x-sinxcosx==-, 此时可得函数的最小正周期. 12.α+β= 【解析】∵sin(2α+β)=sin[(α+β)+α]=sin(α+β)cosα+cos(α+β)sinα=3cos(α+β)sinα, ∴sin(α+β)cosα=2cos(α+β)sinα,即tan(α+β)=2tanα, ∵4tan=1-tan2, ∴=,即tanα=, ∴tan(α+β)=2tanα=1, ∵0<β<, ∴0<<. 故cos. 14.θ是第四象限角 【解析】∵sin=,cos=-, 又由sinθ=2sin?cos=-<0 cosθ=cos2-sin2=>0 故θ是第四象限角. 15.(1) (2) 【解析】(1)∵ ∵a2+b2=4(a+b)-8 ∴(a-2)2+(b-2)2=0 ∴a=2,b=2 由余弦定理得 ∴
一、选择题
1.已知180°<α<360°,则的值等于( )
A. B. C. D.
2.若2sinx=1+cosx,则的值等于( )
A. B.或不存在 C.2 D.2或
3.已知sinα=,<α<π,则tan的值为( )
A. B.-2 C.2 D.
4.已知的值为( )
A. B. C. D.
5.设的值是( )
A. B. C. D.
6.α,β都是锐角,且,,则sinβ的值是( )
A. B. C. D.
7.在△ABC中,若,则△ABC是( )
A.等边三角形 B.等腰三角形 C.不等边三角形 D.直角三角形
8.已知f(x)=sin(3x+θ)-cos(3x+θ)是奇函数且在区间上是减函数,则θ的一个值是( )21教育网
A. B.π C. D.
二、填空题
9.已知,则tanα的值为?? ? .
10.若的值为??? .
11.已知函数f(x)=(sinx-cosx)sinx,x∈R,则f(x)的最小正周期是??? .
三、解答题
12.已知,且sin(2α+β)=3cos(α+β)sinα,,求α+β的值.
13.已知sinα=,sin(α+β)=,α与β均为锐角,求cos.(cos)
14.已知sin=,cos=-,试确定θ的象限.
15.在△ABC中,角A,B,C的对边分别是a,b,c,已知sinC+cosC=1-sin (1)求sinC的值 (2)若?a2+b2=4(a+b)-8,求边c的值.21世纪教育网版权所有
参考答案及解析
1.B 【解析】∵已知180°<α<360°,∴90°<<180°,故>0. ∴=, 2.B 【解析】∵2sinx=1+cosx, ∴2×2sincos=1+(2cos2-1), ∴+==, ∴sinα= ∴cos2α=1-2sin2α=1-2×()2=, 5.B 【解析】==== 6.C 【解析】α,β都是锐角,∴α+β∈(0,π), ∵∴cosα===, ∵ ∴sin(α+β)=== 【解析】tanα===-, 10. 【解析】∵=cos2(+α)=2-1=2-1 =2×-1=, 11.π 【解析】∵f(x)=sin2x-sinxcosx==-, 此时可得函数的最小正周期. 12.α+β= 【解析】∵sin(2α+β)=sin[(α+β)+α]=sin(α+β)cosα+cos(α+β)sinα=3cos(α+β)sinα, ∴sin(α+β)cosα=2cos(α+β)sinα,即tan(α+β)=2tanα, ∵4tan=1-tan2, ∴=,即tanα=, ∴tan(α+β)=2tanα=1, ∵0<β<, ∴0<<. 故cos. 14.θ是第四象限角 【解析】∵sin=,cos=-, 又由sinθ=2sin?cos=-<0 cosθ=cos2-sin2=>0 故θ是第四象限角. 15.(1) (2) 【解析】(1)∵ ∵a2+b2=4(a+b)-8 ∴(a-2)2+(b-2)2=0 ∴a=2,b=2 由余弦定理得 ∴
