3.2.1 古典概型 课件3
图片预览





文档简介
课件16张PPT。3.2.1古典概型一、知识回顾:
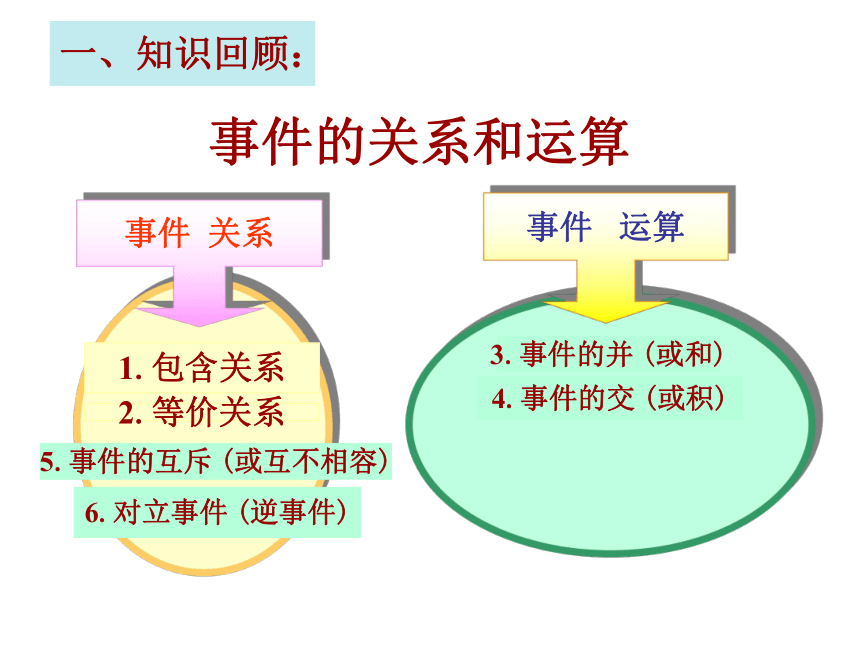
事件 运算事件 关系1.包含关系2.等价关系3.事件的并 (或和)4.事件的交 (或积)事件的关系和运算5.事件的互斥 (或互不相容)6.对立事件 (逆事件)二、概率的几个基本性质(1)、对于任何事件的概率的范围是:
0≤P(A)≤1
其中不可能事件的概率是 P(A)=0
必然事件的概率是 P(A)=1
(2)当事件A与事件B互斥时,A∪B的频率
fn(A∪B)= fn(A)+ fn(B)
由此得到概率的加法公式:二、概率的几个基本性质特别地,当事件A与事件B是对立事件时,有
P(A)=1- P(B)
如果事件A与事件B互斥,则
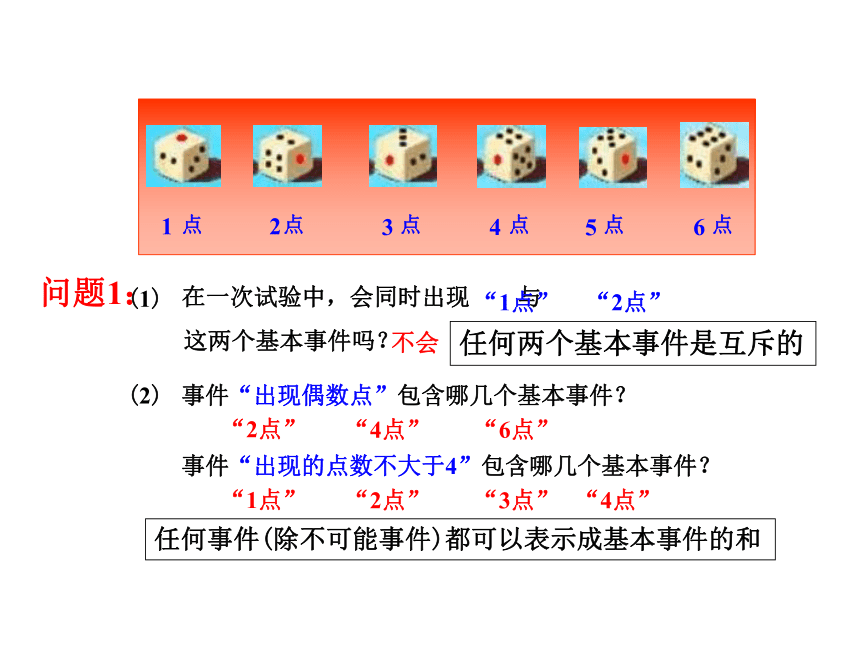
P(A∪B)=P(A)+P(B)试验2:掷一颗均匀的骰子一次,观察出现的点数有哪几种结果?试验1:掷一枚质地均匀的硬币一次,观察出现哪几种结果?2 种6 种新课探究:123456点点点点点点问题1:(1)(2)事件“出现偶数点”包含哪几个基本事件?“2点”“4点”“6点”不会任何两个基本事件是互斥的任何事件(除不可能事件)都可以表示成基本事件的和事件“出现的点数不大于4”包含哪几个基本事件?“1点”“2点”“3点”“4点”基本事件
(1)定义:在一次试验中,所有可能发生的基本结果中不能再分的最简单的随机事件称为该次试验中的基本事件,试验中其他的事件都可以用_____事件来描绘.
(2)基本事件的特点:一是任何两个基本事件是_____的;二是任何事件(除不可能事件)都可以表示成基本事件的____;三是所有基本事件的和事件是必然事件.1.基本互斥和古典概型
(1)定义:如果一个概率模型满足:
①试验中所有可能出现的基本事件只有_____个;
②每个基本事件出现的可能性_____ .
那么这样的概率模型称为古典概率模型,简称为古典概型.
(2)计算公式:对于古典概型,任何事件A的概率为:2.相等有限 (1)向一个圆面内随机地投射一个点,如果该点落在圆内任意一点都是等可能的,你认为这是古典概型吗?为什么? (2)如图,某个水平比较高的同学随机地向一靶心进行射击,这一试验的结果只有有限个:命中10环、命中9环……命中5环和不中环.你认为这是古典概型吗?为什么? 概念升华不是不是你能举出一些古典概型的例子吗?注意: 1.必然事件的概率为1; 2.不可能事件的概率为0;
3. 0≤P(A) ≤1.注意:
1.要判断该概率模型是不是古典概型;
2.要找出随机事件A包含的基本事件的个数和试验中基本事件的总数. 例1: 将一颗均匀的骰子先后抛掷两次,计算:
(1)一共有多少种不同的结果?
(2)其中向上的点数之和是质数的结果有多少种?
[思路探索] 用列举法列出所有结果,然后按要求进行判断即可.
解 (1)将抛掷两次骰子的所有结果一一列举如下:
(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)
(2,1)(2,2)(2,3)(2,4)(2,5)(2,6)
(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)
(4,1)(4,2)(4,3)(4,4)(4,5)(4,6)
(5,1)(5,2)(5,3)(5,4)(5,5)(5,6)
(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)共有36种不同的结果.
(2)总数之和是质数的结果有(1,1),(1,2),(1,4),(1,6),(2,1),(2,3),(2,5),(3,2),(3,4),(4,1),(4,3),(5,2),(5,6),(6,1),(6,5)共15种.对于两个变量或两次试验找基本事件的方法(列表) 变式一:连续掷3枚硬币,观察落地后这3枚硬币出现正面还是反面:
(1)写出这个试验的所有基本事件;
(2)求这个试验的基本事件的总数;
(3)记A=“恰有两枚正面向上”这一事件,则A包含哪几个基本事件?
解 (1)这个试验的基本事件集合为:(2)基本事件的总数是8.
(3)“恰有两枚正面向上”包含以下3个基本事件:(正,正,反),(正,反,正),(反,正,正).
正正反正正正正正反反反反反反对于三个(或以上)变量或三次(或以上)试验找基本事件的方法(树状图)例.单选题是标准化考试中常用的题型,一般是从、、、四个选项中选择一个正确的答案.假设考生不会做,他随机地选择了一个答案,则他答对的概率为如果该题是不定项选择题,假如考生也不会做,则他能够答对的概率为多少?探究:此时比单选题容易了,还是更难了?基本事件有15个:ABCDABACADBCBDCDABCABDBCDABCDACD“答对”包含的基本事件数:1P(“答对”)这节课你学到了哪些知识?1、基本事件、古典概型的定义2、古典概型的概率计算公式3.计算古典概型中的随机事件A的概率的步骤: (1)审清题意,判断本试验中的基本事件是否满足等可能性.(2)计算所有基本事件的总数(3)计算事件A所包含的基本事件数假设储蓄卡的密码由4个数字组成,每个数字可以是0,1,2,3,4,5,6,7,8,9十个数字中的任意一个,假设一个人完全不知道这张卡的密码,则他到自动取款机上随机试一次密码就能取到钱的概率是多少?〖解〗每个密码相当于一个基本事件,共有10000个基本事件,即0000,0001,0002,…,9999.是一个古典概型.其中事件A“试一次密码就能取到钱”由1个基本事件构成.所以:
事件 运算事件 关系1.包含关系2.等价关系3.事件的并 (或和)4.事件的交 (或积)事件的关系和运算5.事件的互斥 (或互不相容)6.对立事件 (逆事件)二、概率的几个基本性质(1)、对于任何事件的概率的范围是:
0≤P(A)≤1
其中不可能事件的概率是 P(A)=0
必然事件的概率是 P(A)=1
(2)当事件A与事件B互斥时,A∪B的频率
fn(A∪B)= fn(A)+ fn(B)
由此得到概率的加法公式:二、概率的几个基本性质特别地,当事件A与事件B是对立事件时,有
P(A)=1- P(B)
如果事件A与事件B互斥,则
P(A∪B)=P(A)+P(B)试验2:掷一颗均匀的骰子一次,观察出现的点数有哪几种结果?试验1:掷一枚质地均匀的硬币一次,观察出现哪几种结果?2 种6 种新课探究:123456点点点点点点问题1:(1)(2)事件“出现偶数点”包含哪几个基本事件?“2点”“4点”“6点”不会任何两个基本事件是互斥的任何事件(除不可能事件)都可以表示成基本事件的和事件“出现的点数不大于4”包含哪几个基本事件?“1点”“2点”“3点”“4点”基本事件
(1)定义:在一次试验中,所有可能发生的基本结果中不能再分的最简单的随机事件称为该次试验中的基本事件,试验中其他的事件都可以用_____事件来描绘.
(2)基本事件的特点:一是任何两个基本事件是_____的;二是任何事件(除不可能事件)都可以表示成基本事件的____;三是所有基本事件的和事件是必然事件.1.基本互斥和古典概型
(1)定义:如果一个概率模型满足:
①试验中所有可能出现的基本事件只有_____个;
②每个基本事件出现的可能性_____ .
那么这样的概率模型称为古典概率模型,简称为古典概型.
(2)计算公式:对于古典概型,任何事件A的概率为:2.相等有限 (1)向一个圆面内随机地投射一个点,如果该点落在圆内任意一点都是等可能的,你认为这是古典概型吗?为什么? (2)如图,某个水平比较高的同学随机地向一靶心进行射击,这一试验的结果只有有限个:命中10环、命中9环……命中5环和不中环.你认为这是古典概型吗?为什么? 概念升华不是不是你能举出一些古典概型的例子吗?注意: 1.必然事件的概率为1; 2.不可能事件的概率为0;
3. 0≤P(A) ≤1.注意:
1.要判断该概率模型是不是古典概型;
2.要找出随机事件A包含的基本事件的个数和试验中基本事件的总数. 例1: 将一颗均匀的骰子先后抛掷两次,计算:
(1)一共有多少种不同的结果?
(2)其中向上的点数之和是质数的结果有多少种?
[思路探索] 用列举法列出所有结果,然后按要求进行判断即可.
解 (1)将抛掷两次骰子的所有结果一一列举如下:
(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)
(2,1)(2,2)(2,3)(2,4)(2,5)(2,6)
(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)
(4,1)(4,2)(4,3)(4,4)(4,5)(4,6)
(5,1)(5,2)(5,3)(5,4)(5,5)(5,6)
(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)共有36种不同的结果.
(2)总数之和是质数的结果有(1,1),(1,2),(1,4),(1,6),(2,1),(2,3),(2,5),(3,2),(3,4),(4,1),(4,3),(5,2),(5,6),(6,1),(6,5)共15种.对于两个变量或两次试验找基本事件的方法(列表) 变式一:连续掷3枚硬币,观察落地后这3枚硬币出现正面还是反面:
(1)写出这个试验的所有基本事件;
(2)求这个试验的基本事件的总数;
(3)记A=“恰有两枚正面向上”这一事件,则A包含哪几个基本事件?
解 (1)这个试验的基本事件集合为:(2)基本事件的总数是8.
(3)“恰有两枚正面向上”包含以下3个基本事件:(正,正,反),(正,反,正),(反,正,正).
正正反正正正正正反反反反反反对于三个(或以上)变量或三次(或以上)试验找基本事件的方法(树状图)例.单选题是标准化考试中常用的题型,一般是从、、、四个选项中选择一个正确的答案.假设考生不会做,他随机地选择了一个答案,则他答对的概率为如果该题是不定项选择题,假如考生也不会做,则他能够答对的概率为多少?探究:此时比单选题容易了,还是更难了?基本事件有15个:ABCDABACADBCBDCDABCABDBCDABCDACD“答对”包含的基本事件数:1P(“答对”)这节课你学到了哪些知识?1、基本事件、古典概型的定义2、古典概型的概率计算公式3.计算古典概型中的随机事件A的概率的步骤: (1)审清题意,判断本试验中的基本事件是否满足等可能性.(2)计算所有基本事件的总数(3)计算事件A所包含的基本事件数假设储蓄卡的密码由4个数字组成,每个数字可以是0,1,2,3,4,5,6,7,8,9十个数字中的任意一个,假设一个人完全不知道这张卡的密码,则他到自动取款机上随机试一次密码就能取到钱的概率是多少?〖解〗每个密码相当于一个基本事件,共有10000个基本事件,即0000,0001,0002,…,9999.是一个古典概型.其中事件A“试一次密码就能取到钱”由1个基本事件构成.所以:
