3.1.1和3.1.2 随机事件的概率及其意义 课件
文档属性
| 名称 | 3.1.1和3.1.2 随机事件的概率及其意义 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 346.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-06 00:00:00 | ||
图片预览





文档简介
课件16张PPT。3.1.1~3.1.2
随机事件的概率及其意义【学习目标】
(1)了解随机事件、必然事件、不可能事件的概念;
(2)正确理解事件A出现的频率的意义;
(3)正确理解概率的概念和意义,明确事件A发生的频率fn(A)与事件A发生的概率P(A)的区别与联系;
(4)利用概率知识正确理解现实生活中的实际问题.
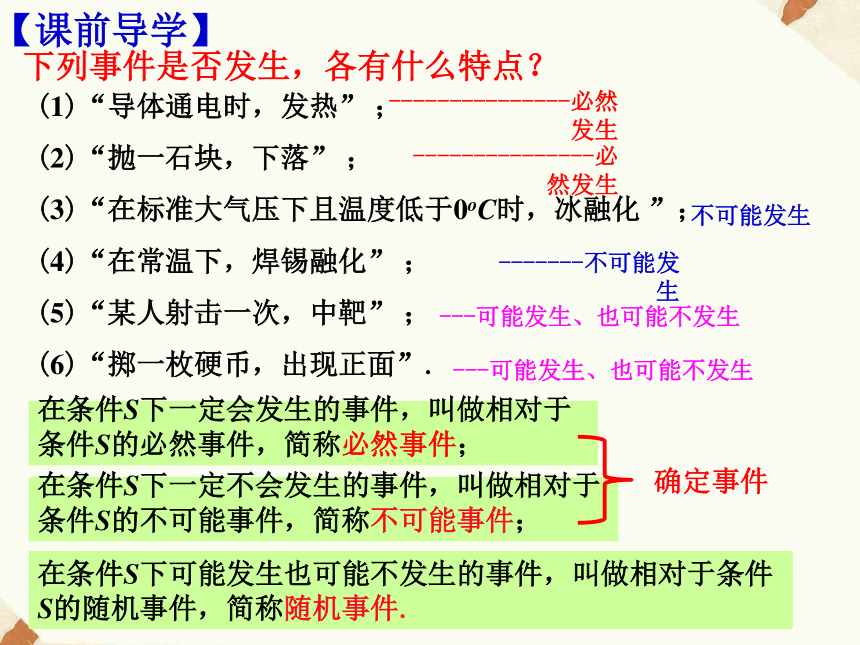
【课前导学】(1)“导体通电时,发热” ;
(2)“抛一石块,下落” ;
(3)“在标准大气压下且温度低于0oC时,冰融化 ”;
(4)“在常温下,焊锡融化” ;
(5)“某人射击一次,中靶” ;
(6)“掷一枚硬币,出现正面”.下列事件是否发生,各有什么特点?---------------必然发生---------------必然发生不可能发生-------不可能发生---可能发生、也可能不发生---可能发生、也可能不发生在条件S下一定会发生的事件,叫做相对于
条件S的必然事件,简称必然事件;在条件S下一定不会发生的事件,叫做相对于
条件S的不可能事件,简称不可能事件;在条件S下可能发生也可能不发生的事件,叫做相对于条件S的随机事件,简称随机事件.确定事件让我们来做抛掷硬币试验【规则(1)硬币统一(1元硬币);(2)垂直下抛;(3)离桌面高度大约为30cm.】2.试验、观察和归纳2、思考与讨论: 1.对于给定的事件A,在相同条件下重复n次试验,观察A是否出现,称事件A出现的次数n为事件A出现的 ,事件A出现的次数nA
与总实验次数n的比例 叫做事件A出现的 .
2.?必然事件的频率为 ,不可能事件的频率为 ,频率的取值范围是 .(为什么?)
3.试验结果与其他同学比较,你的结果和他们一致吗?为什么?
4.如果我们来做大量的重复抛掷硬币的试验,正面朝上的频率值会有什么规律吗?
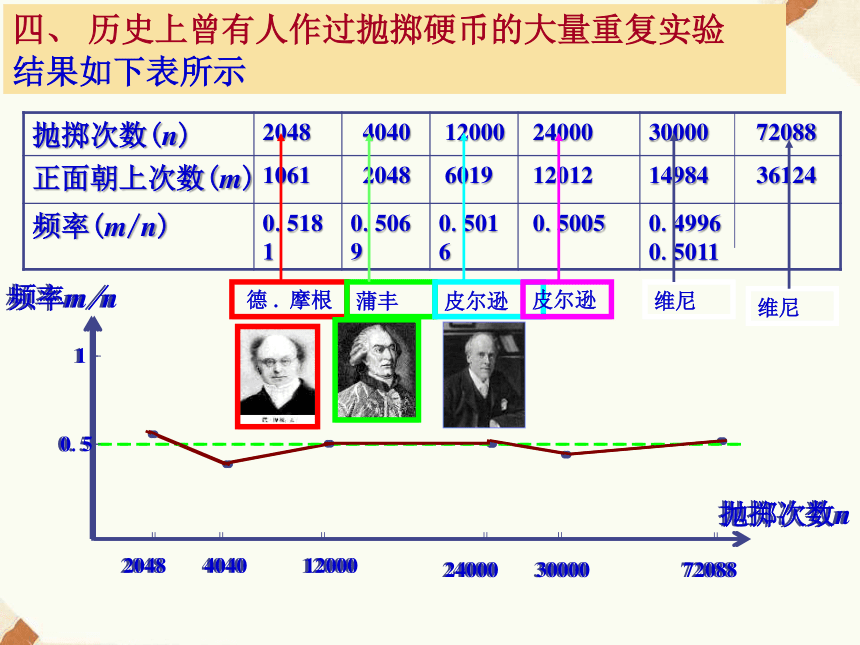
因为“抛掷一枚硬币,正面朝上”这个事件是一个随机事件,在每一次试验中,它的结果是随机的,所以10次的试验结果也是随机的,可能会不同. 频数频率fn(A)[0,1]10四、 历史上曾有人作过抛掷硬币的大量重复实验
结果如下表所示德 . 摩根蒲丰皮尔逊皮尔逊 维尼维尼 一般来说,随机事件A在每次试验中是否发生是不能预知的,但在大量重复试验后,随着试验次数的增加,事件A发生的频率会稳定在区间 [0,1] 中的某个常数上. 我们就用这个常数来度量事件A发生的可能性的大小,这个常数就叫做随机事件A的概率,用 表示.概率的定义 这个常数越接近于1,表明事件A发生的频率越大,频数就越多,也就是它发生的可能性越大;反过来,事件发生的可能性越小,频数就越少,频率就越小,这个常数就越小.【课前导学】(1)随着试验次数的增加,频率会越来越接近概率;
(2)频率本身是随机的,在试验前不能确定;
(3)概率是一个确定的数,是客观存在的,与每次试验无关;
(4)概率是频率的稳定值,而频率是概率的近似值.5、概率与频率的关系: 因此在实际中我们求一个事件的概率时,有时通过进行大量的重复试验,用这个事件发生的频率近似地作为它的概率.【课内探究】例1、某射手在同一条件下进行射击,结果如下表所示:
(1)填写表中击中靶心的频率;
(2)这个射手射击一次,击中靶心的概率约是什么?
0.80.950.880.920.890.91(2)这个射手射击一次,击中靶心的概率约是0.9 随机事件在一次实验中发生与否是随机的,但随机性中含有规律性:即随着实验次数的增加,该随机事件发生的频率会越来越接近于该事件发生的概率.认识了这种随机性中的规律性,就能使我们比较准确地预测随机事件发生的可能性.【课内探究】例2、某校共有学生12000人,学校为使学生增强交通安全观念,准备随机抽查12名学生进行交通安全知识测试,其中某学生认为抽查的几率为1/1000,不可能抽查到他,所以不再准备交通安全知识以便应试,你认为他的做法对吗?并说明理由.如果该校高三年级理科班恰好有1000人,那么高三年级理科班一定有1名学生被抽中吗?
变式1:生活中,我们经常听到这样的议论:“天气预报说昨天降水概率为90%,结果根本一点雨都没下,天气预报也太不准确了.”学了概率后,你能给出解释吗?
在一次试验中,概率为90%的事件也可能不出现.因此昨天没有下雨并不能说明“昨天降水的概率为90%”的天气预报是错误的.不对;虽然抽到的概率为0.001,但也有可能抽到他.不一定;高三年级有1000人,相当于做1000次试验,因为每次试验的结果都是随机的,所以做1000次的结果也是随机的.这就是说虽然高三理科有1000人,也可能1名学生都没被抽中.【课内探究】变式2:设有外形完全相同的两个箱子,甲箱有99个白球1个黑球,乙箱有1个白球99个黑球,随机抽取一箱,再从取出的一箱中抽取一球,结果取得白球,问此球最有可能是从哪个箱子中取出的?为什么??
解:甲箱中有99个白球1个黑球,故随机地取出一球,得白球的可能性是0.99,乙箱中有1个白球和99个黑球,从中任取一球,得白球的可能性是0.01,由此看到,这一白球从甲箱中抽出的概率比从乙箱中抽出的概率大得多.由极大似然法,既然在一次抽样中抽得白球,当然可以认为是由概率大的箱子中抽出的.所以我们作出推断是从甲箱中抽出的.?
如果我们面临的是从多个可选答案中挑选正确答案的决策任务,那么“使得样本出现的可能性最大”可以作为决策的准则,这种判断问题的方法称为极大似然法.【方法总结】2.概率是频率的稳定值,根据随机事件发生的频率只能得到概率的估计值.3.随机事件A在每次试验中是否发生是不能预知的,但是在大量重复试验后,随着试验次数的增加,事件A发生的频率逐渐稳定在区间[0,1]内的某个常数上(即事件A的概率).4.概率是描述随机事件发生的可能性大小的一个数量,即使是大概率事件,也不能肯定事件一定会发生,只是认为事件发生的可能性大.1.事件的分类:必然事件、不可能事件、随机事件.豌豆杂交试验的子二代结果遗传机理中的统计规律第二代第一代亲 本YY 表示纯黄色的豌豆 yy 表示纯绿色的豌豆
(其中Y为显性因子 y为隐性因子)黄色豌豆(YY,Yy):绿色豌豆(yy)
≈ 3 : 1【反馈检测】1、从12个同类产品(其中有10个正品,2个次品)中,任意取3个的必然事件是
A.3个都是正品 B.至少有1个是次品
C.3个都是次品 D.至少有1个是正品
2、在天气预报中,有“降水概率预报”,例如预报“明天降水概率为85%”,这是说( )
A.明天该 地区有85%的地区降水,其他15%的地区不降水
B.明天该地区约有85%的时间降水,其他时间不降水
C.气象台的专家中,有85%的人认为会降水,另外15%的专家认为不降水
D.明天该地区的降水的可能性 为85%
3、从一批准 备出厂的电视机中随机抽取10台进行质量检查,其中有一台是次品, 若用A表示抽到次品这一事件,则对A的说法正确的是( )
A.概率为1/10 B.频率为1/10
C.概率接近1/10 D.每抽10台电视机必有1台次品DDB4、每道选择题有4个选项,其中只有1个选项是正确的.某次考试12道选择题,某人说:“每个选项正确的概率是0.25,我每题都选A,则一定有3道题选择结果正确”这句话( )
A.正确 B.错误 C.不一定 D.无法解释
5、先后抛掷两枚均匀的一分?贰分的硬币,观察落地后硬币的正反面情况,则哪个事件的概率最大( )
A.至少一枚硬币正面向上
B.只有一枚硬币正面向上
C.两枚硬币都是正面向上
D.两枚硬币一枚正面向上,另一枚反面向上BA【反馈检测】6、某中学高一年级有12个班,要从中选2个班代表学校参加某项活动.由于某种原因,一班必须参加,另外再从二至十二班中选1个班.有人提议用如下的方法:掷两个骰子得到的点数和是几,就选几班,你认为这种方法公平吗?哪个班被选中的概率最大?7、一个地区从某年起几年之内的新生儿数及其中男婴数如下:(1)填写表中男婴出生的频率(结果保留到小数点后第3位);(2)这一地区男婴出生的概率约是多少?不公平.7班被选中的概率最大.0.517
(1)了解随机事件、必然事件、不可能事件的概念;
(2)正确理解事件A出现的频率的意义;
(3)正确理解概率的概念和意义,明确事件A发生的频率fn(A)与事件A发生的概率P(A)的区别与联系;
(4)利用概率知识正确理解现实生活中的实际问题.
【课前导学】(1)“导体通电时,发热” ;
(2)“抛一石块,下落” ;
(3)“在标准大气压下且温度低于0oC时,冰融化 ”;
(4)“在常温下,焊锡融化” ;
(5)“某人射击一次,中靶” ;
(6)“掷一枚硬币,出现正面”.下列事件是否发生,各有什么特点?---------------必然发生---------------必然发生不可能发生-------不可能发生---可能发生、也可能不发生---可能发生、也可能不发生在条件S下一定会发生的事件,叫做相对于
条件S的必然事件,简称必然事件;在条件S下一定不会发生的事件,叫做相对于
条件S的不可能事件,简称不可能事件;在条件S下可能发生也可能不发生的事件,叫做相对于条件S的随机事件,简称随机事件.确定事件让我们来做抛掷硬币试验【规则(1)硬币统一(1元硬币);(2)垂直下抛;(3)离桌面高度大约为30cm.】2.试验、观察和归纳2、思考与讨论: 1.对于给定的事件A,在相同条件下重复n次试验,观察A是否出现,称事件A出现的次数n为事件A出现的 ,事件A出现的次数nA
与总实验次数n的比例 叫做事件A出现的 .
2.?必然事件的频率为 ,不可能事件的频率为 ,频率的取值范围是 .(为什么?)
3.试验结果与其他同学比较,你的结果和他们一致吗?为什么?
4.如果我们来做大量的重复抛掷硬币的试验,正面朝上的频率值会有什么规律吗?
因为“抛掷一枚硬币,正面朝上”这个事件是一个随机事件,在每一次试验中,它的结果是随机的,所以10次的试验结果也是随机的,可能会不同. 频数频率fn(A)[0,1]10四、 历史上曾有人作过抛掷硬币的大量重复实验
结果如下表所示德 . 摩根蒲丰皮尔逊皮尔逊 维尼维尼 一般来说,随机事件A在每次试验中是否发生是不能预知的,但在大量重复试验后,随着试验次数的增加,事件A发生的频率会稳定在区间 [0,1] 中的某个常数上. 我们就用这个常数来度量事件A发生的可能性的大小,这个常数就叫做随机事件A的概率,用 表示.概率的定义 这个常数越接近于1,表明事件A发生的频率越大,频数就越多,也就是它发生的可能性越大;反过来,事件发生的可能性越小,频数就越少,频率就越小,这个常数就越小.【课前导学】(1)随着试验次数的增加,频率会越来越接近概率;
(2)频率本身是随机的,在试验前不能确定;
(3)概率是一个确定的数,是客观存在的,与每次试验无关;
(4)概率是频率的稳定值,而频率是概率的近似值.5、概率与频率的关系: 因此在实际中我们求一个事件的概率时,有时通过进行大量的重复试验,用这个事件发生的频率近似地作为它的概率.【课内探究】例1、某射手在同一条件下进行射击,结果如下表所示:
(1)填写表中击中靶心的频率;
(2)这个射手射击一次,击中靶心的概率约是什么?
0.80.950.880.920.890.91(2)这个射手射击一次,击中靶心的概率约是0.9 随机事件在一次实验中发生与否是随机的,但随机性中含有规律性:即随着实验次数的增加,该随机事件发生的频率会越来越接近于该事件发生的概率.认识了这种随机性中的规律性,就能使我们比较准确地预测随机事件发生的可能性.【课内探究】例2、某校共有学生12000人,学校为使学生增强交通安全观念,准备随机抽查12名学生进行交通安全知识测试,其中某学生认为抽查的几率为1/1000,不可能抽查到他,所以不再准备交通安全知识以便应试,你认为他的做法对吗?并说明理由.如果该校高三年级理科班恰好有1000人,那么高三年级理科班一定有1名学生被抽中吗?
变式1:生活中,我们经常听到这样的议论:“天气预报说昨天降水概率为90%,结果根本一点雨都没下,天气预报也太不准确了.”学了概率后,你能给出解释吗?
在一次试验中,概率为90%的事件也可能不出现.因此昨天没有下雨并不能说明“昨天降水的概率为90%”的天气预报是错误的.不对;虽然抽到的概率为0.001,但也有可能抽到他.不一定;高三年级有1000人,相当于做1000次试验,因为每次试验的结果都是随机的,所以做1000次的结果也是随机的.这就是说虽然高三理科有1000人,也可能1名学生都没被抽中.【课内探究】变式2:设有外形完全相同的两个箱子,甲箱有99个白球1个黑球,乙箱有1个白球99个黑球,随机抽取一箱,再从取出的一箱中抽取一球,结果取得白球,问此球最有可能是从哪个箱子中取出的?为什么??
解:甲箱中有99个白球1个黑球,故随机地取出一球,得白球的可能性是0.99,乙箱中有1个白球和99个黑球,从中任取一球,得白球的可能性是0.01,由此看到,这一白球从甲箱中抽出的概率比从乙箱中抽出的概率大得多.由极大似然法,既然在一次抽样中抽得白球,当然可以认为是由概率大的箱子中抽出的.所以我们作出推断是从甲箱中抽出的.?
如果我们面临的是从多个可选答案中挑选正确答案的决策任务,那么“使得样本出现的可能性最大”可以作为决策的准则,这种判断问题的方法称为极大似然法.【方法总结】2.概率是频率的稳定值,根据随机事件发生的频率只能得到概率的估计值.3.随机事件A在每次试验中是否发生是不能预知的,但是在大量重复试验后,随着试验次数的增加,事件A发生的频率逐渐稳定在区间[0,1]内的某个常数上(即事件A的概率).4.概率是描述随机事件发生的可能性大小的一个数量,即使是大概率事件,也不能肯定事件一定会发生,只是认为事件发生的可能性大.1.事件的分类:必然事件、不可能事件、随机事件.豌豆杂交试验的子二代结果遗传机理中的统计规律第二代第一代亲 本YY 表示纯黄色的豌豆 yy 表示纯绿色的豌豆
(其中Y为显性因子 y为隐性因子)黄色豌豆(YY,Yy):绿色豌豆(yy)
≈ 3 : 1【反馈检测】1、从12个同类产品(其中有10个正品,2个次品)中,任意取3个的必然事件是
A.3个都是正品 B.至少有1个是次品
C.3个都是次品 D.至少有1个是正品
2、在天气预报中,有“降水概率预报”,例如预报“明天降水概率为85%”,这是说( )
A.明天该 地区有85%的地区降水,其他15%的地区不降水
B.明天该地区约有85%的时间降水,其他时间不降水
C.气象台的专家中,有85%的人认为会降水,另外15%的专家认为不降水
D.明天该地区的降水的可能性 为85%
3、从一批准 备出厂的电视机中随机抽取10台进行质量检查,其中有一台是次品, 若用A表示抽到次品这一事件,则对A的说法正确的是( )
A.概率为1/10 B.频率为1/10
C.概率接近1/10 D.每抽10台电视机必有1台次品DDB4、每道选择题有4个选项,其中只有1个选项是正确的.某次考试12道选择题,某人说:“每个选项正确的概率是0.25,我每题都选A,则一定有3道题选择结果正确”这句话( )
A.正确 B.错误 C.不一定 D.无法解释
5、先后抛掷两枚均匀的一分?贰分的硬币,观察落地后硬币的正反面情况,则哪个事件的概率最大( )
A.至少一枚硬币正面向上
B.只有一枚硬币正面向上
C.两枚硬币都是正面向上
D.两枚硬币一枚正面向上,另一枚反面向上BA【反馈检测】6、某中学高一年级有12个班,要从中选2个班代表学校参加某项活动.由于某种原因,一班必须参加,另外再从二至十二班中选1个班.有人提议用如下的方法:掷两个骰子得到的点数和是几,就选几班,你认为这种方法公平吗?哪个班被选中的概率最大?7、一个地区从某年起几年之内的新生儿数及其中男婴数如下:(1)填写表中男婴出生的频率(结果保留到小数点后第3位);(2)这一地区男婴出生的概率约是多少?不公平.7班被选中的概率最大.0.517
