3.1.3 概率的基本性质 课件
文档属性
| 名称 | 3.1.3 概率的基本性质 课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 649.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-06 00:00:00 | ||
图片预览








文档简介
课件23张PPT。3.1.3 概率的基本性质事件
的关系
和运算
概率的
几个基
本性质
比如在掷骰子这个试验中:“出现的点数小于或等于3”这个事件中包含了哪些结果呢?①“出现的点数为1” ;
②“出现的点数为2” ;
③“出现的点数为3”这三个结果一.创设情境,引入新课 上一节课我们学习了随机事件的概率,举了生活中与概率知识有关的许多实例.今天我们来研究
概率的基本性质.在研究性质之前,我们先来研究一下事件之间有什么关系. 你能写出在掷骰子的试验中出现的其它事件吗?C1 ={出现1点};C2={出现2点}; C3={出现3点};
C4 ={出现4点};C5={出现5点}; C6={出现6点};上述事件中有必然事件或不可能事件吗?有的
话,哪些是?D1={出现的点数不大于1}; D2={出现的点数大于3};
D3={出现的点数小于5}; E={出现的点数小于7};
F={出现的点数大于6}; G={出现的点数为偶数};
H={出现的点数为奇数};……一.创设情境,引入新课2. 若事件C1发生,则还有哪些事件也一定会发生?
反过来可以吗?3.上述事件中,哪些事件发生会使得 K={出现1
点或5点}也发生?6.在掷骰子实验中事件G和事件H是否一定有一个
会发生?5.若只掷一次骰子,则事件C1和事件C2有可能同
时发生么?4.上述事件中,哪些事件发生当且仅当事件D2且事
件D3同时发生?(一)事件的关系和运算:BA如图:例.事件C1 ={出现1点 }发生,则事件 H ={出现的点数为奇数}也一定会发生,所以注:不可能事件记作 ,任何事件都包括不可能事件.(1)包含关系 一般地,对于事件A与事件B,如果事件A发生,则事件B一定发生,这时称事件B包含事件A(或称事件A包含于事件B),记作二.剖析概念,夯实基础(2)相等关系B A如图:例.事件C1={出现1点}发生,则事件D1={出现的点数不大于1}就一定会发生,反过来也一样,所以C1=D1.一般地,对事件A与事件B,若 ,那么称事件A与事件B相等,记作A=B .二.剖析概念,夯实基础(3)并事件(和事件)若某事件发生当且仅当事件A发生或事件B发生,则称此事件为事件A和事件B的并事件(或和事件),记作 .B A如图:例.若事件K={出现1点或5点} 发生,则事件C1 =
{出现1点}与事件C5 ={出现 5 点 }中至少有一个会
发生,则 二.剖析概念,夯实基础(4)交事件(积事件)若某事件发生当且仅当事件A发生且事件B发生,则称此事件为事件A和事件B的交事件(或积事件)记作 B A如图:例.若事件 M={出现1点且5点}发生,则事件C1 ={出现1点}与事件C5 ={出现5点}同时发生,则 二.剖析概念,夯实基础(5)互斥事件若 为不可能事件( ),那么称事件A与事件B互斥,其含义是:事件A与事件B在任何一次试验中都不会同时发生.AB如图:例.因为事件C1={出现1点}与事件C2={出现2点}
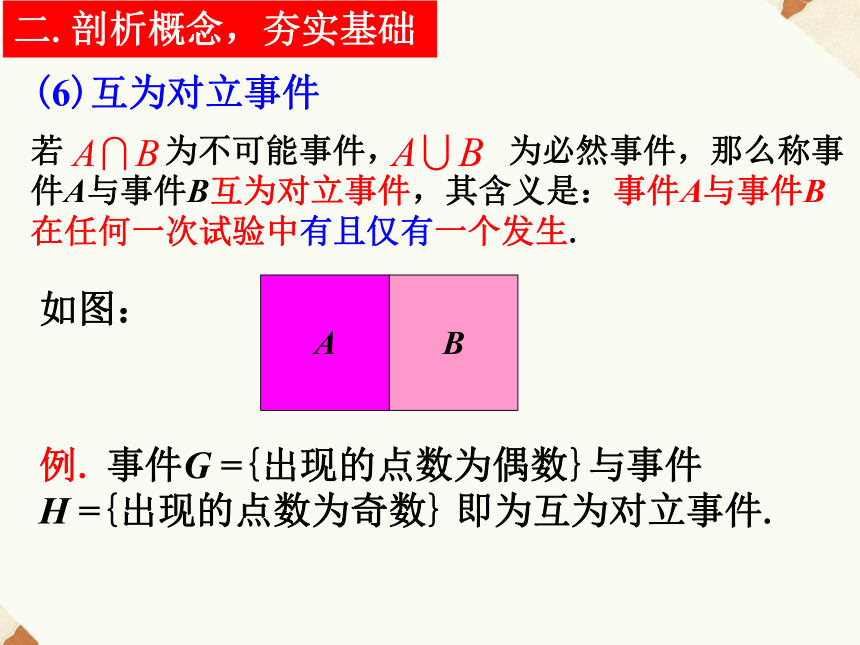
不可能同时发生,故这两个事件互斥.二.剖析概念,夯实基础(6)互为对立事件若 为不可能事件, 为必然事件,那么称事件A与事件B互为对立事件,其含义是:事件A与事件B在任何一次试验中有且仅有一个发生.如图:例. 事件G ={出现的点数为偶数}与事件
H ={出现的点数为奇数} 即为互为对立事件.二.剖析概念,夯实基础①互斥事件可以是两个或两个以上事件的关系,
而对立事件只针对两个事件而言.②从定义上看,两个互斥事件有可能都不发生,也可能有一个发生,也就是不可能同时发生;
而对立事件除了要求这两个事件不同时发生外,还要求这二者之间必须要有一个发生,因此,对立事件是互斥事件,是互斥事件的特殊情况,但互斥事件不一定是对立事件.③从集合角度看,几个事件彼此互斥,是指这几个事件所包含的结果组成的集合的交集为空集;而事件A的对立事件所包含的结果组成的集合是全集中由事件A所包含的结果组成的集合的补集.
互斥事件与对立事件的区别:事件与集合之间的对应关系1.概率P(A)的取值范围(1)0≤P(A)≤1.(2)必然事件的概率是1.(3)不可能事件的概率是0.(4)若A B, 则 P(A) ≤P(B)(二)概率的基本性质二.剖析概念,夯实基础思考:掷一枚骰子,事件C1={出现1点},事件
C3={出现3点}则事件C1 ? C3 发生的频率
与事件C1和事件C3发生的频率之间有什
么关系?结论:当事件A与事件B互斥时
二.剖析概念,夯实基础2.概率的加法公式:如果事件A与事件B互斥,则
P (A ? B)= P (A) + P (B)若事件A,B为对立事件,则
P(B)=1-P(A)3.对立事件的概率公式二.剖析概念,夯实基础注意:1.利用上述公式求概率是,首先要确定
两事件是否互斥,如果没有这一条件,该公式
不能运用.即当两事件不互斥时,应有:如果事件A与事件B互斥,则
P (A ? B)= P (A) + P (B)P (A ? B)= P (A) + P (B) - P(???)2.上述公式可推广,即如果随机事件A1,A2,
……,An中任何两个都是互斥事件,那么有P (A1 ? A2 ?… ?An)= P (A1) + P (A2)+…+P(?n)一般地,在解决比较复杂的事件的概率问题时,常常把复杂事件分解为几个互斥事件,借助该推广公式解决.事件B:命中环数为10环;
事件C:命中环数小于6环.
事件D:命中环数为6、7、8、9、10环
2、从40张扑克牌(红桃、黑桃、方块和梅花点数从1-10各10张)中,任取一张.课中探究1、一个射手进行一次射击:
事件A:命中环数大于7环;例1:试判断下列事件哪些是互斥事件?哪些是对立事件?(1)“抽出红桃”与“抽出黑桃”;
(2)“抽出红色牌”与“抽出黑色牌”;
(3)“抽出点数为5的倍数”与“抽出的点数大于9”;
解:互斥事件有:A和C、B和C、C和D.
对立事件有:C和D.解:互斥事件有:(1)、(2) ;对立事件有:(2)课中探究例2:袋中有12个小球,分别为红球、黑球、黄球、绿球,从中任取一球,得到红球的概率为 ,得到黑球或黄球的概率是 ,得到黄球或绿球的概率也是 ,试求得到黑球、得到黄球、得到绿球的概率各是多少?分析:利用方程的思想及互斥事件、对立事件的概率公式求解 有P(B∪C)=P(B)+P(C)= ;
P(C∪D)=P(C)+P(D)= ;
P(B∪C∪D)=1-P(A)=1- = ,
解得P(B)= ,P(C)= ,P(D)= 解:从袋中任取一球,记事件“摸到红球”、“摸到黑球”、“摸到黄球”、“摸到绿球”为A、B、C、D,则1、事件的关系与运算,区分互斥事件与对立事件小结提升2.概率的基本性质:
1)必然事件概率为1,不可能事件概率为0,因此0≤P(A)≤1;
2)当事件A与B互斥时,满足加法公式:P(A∪B)= P(A)+ P(B);
3)若事件A与B为对立事件,则A∪B为必然事件,所以P(A∪B)= P(A)+ P(B)=1,于是有P(A)=1-P(B);小结提升B反馈检测1、(4)一个人打靶时连续射击两次,事件“至少有一次中靶”的互斥事件是( )
(A)至少有一次中靶.(B)两次都中靶.
(C)只有一次中靶. (D)两次都不中靶.
(5)把红、蓝、黑、白4张纸牌随机分给甲、乙、丙、丁4个人,每人分得一张,事件“甲分得红牌”与事件“乙分得红牌”是( )
(A)对立事件 . (B)互斥但不对立事件.
(C)不可能事件 .( D)以上都不是.
D课本121页B2.抽查10件产品,设事件A:至少有两件次品,则A的对立事件为( )
A. 至多两件次品 B. 至多一件次品
C. 至多两件正品 D. 至少两件正品3.某产品分甲、乙、丙三级,其中乙、丙两级均属次品,若生产中出现乙级品的概率为0.03、丙级品的概率为0.01,则对成品抽查一件抽得正品的概率为( )
A.0.09 B.0.98 C.0.97 D.0.96D4、某射手射击一次射中10环,9环,8环,7环的概率是0.24,0.28,0.19,0.16,计算这名射手射击一次:(1)射中10环或9环的概率;
(2)至少射中7环的概率.(1) P(A∪B)=P(A)+P(B) =0.24+0.28=0.52.(2) 因为它们是互斥事件,所以至少射中7环的概率是0.24+0.28+0.19+0.16=0.875、甲,乙两人下棋,和棋的概率为1/2,乙获胜的概率为1/3,求:(1)甲获胜的概率;(2)甲不输的概率.分析:甲乙两人下棋,其结果有甲胜、和棋、乙胜三种,它们是互斥事件.解:(1)“甲获胜”是“和棋或乙胜”的对立事件,所以甲获胜的概率是P=1-1/2-1/3=1/6.(2)解法1:“甲不输”看作是“甲胜”,“和棋”这两个事件的并事件所以P=1/6+1/2=2/3.
解法2:“甲不输”看作是“乙胜”的对立事件,P=1-1/3=2/3.
的关系
和运算
概率的
几个基
本性质
比如在掷骰子这个试验中:“出现的点数小于或等于3”这个事件中包含了哪些结果呢?①“出现的点数为1” ;
②“出现的点数为2” ;
③“出现的点数为3”这三个结果一.创设情境,引入新课 上一节课我们学习了随机事件的概率,举了生活中与概率知识有关的许多实例.今天我们来研究
概率的基本性质.在研究性质之前,我们先来研究一下事件之间有什么关系. 你能写出在掷骰子的试验中出现的其它事件吗?C1 ={出现1点};C2={出现2点}; C3={出现3点};
C4 ={出现4点};C5={出现5点}; C6={出现6点};上述事件中有必然事件或不可能事件吗?有的
话,哪些是?D1={出现的点数不大于1}; D2={出现的点数大于3};
D3={出现的点数小于5}; E={出现的点数小于7};
F={出现的点数大于6}; G={出现的点数为偶数};
H={出现的点数为奇数};……一.创设情境,引入新课2. 若事件C1发生,则还有哪些事件也一定会发生?
反过来可以吗?3.上述事件中,哪些事件发生会使得 K={出现1
点或5点}也发生?6.在掷骰子实验中事件G和事件H是否一定有一个
会发生?5.若只掷一次骰子,则事件C1和事件C2有可能同
时发生么?4.上述事件中,哪些事件发生当且仅当事件D2且事
件D3同时发生?(一)事件的关系和运算:BA如图:例.事件C1 ={出现1点 }发生,则事件 H ={出现的点数为奇数}也一定会发生,所以注:不可能事件记作 ,任何事件都包括不可能事件.(1)包含关系 一般地,对于事件A与事件B,如果事件A发生,则事件B一定发生,这时称事件B包含事件A(或称事件A包含于事件B),记作二.剖析概念,夯实基础(2)相等关系B A如图:例.事件C1={出现1点}发生,则事件D1={出现的点数不大于1}就一定会发生,反过来也一样,所以C1=D1.一般地,对事件A与事件B,若 ,那么称事件A与事件B相等,记作A=B .二.剖析概念,夯实基础(3)并事件(和事件)若某事件发生当且仅当事件A发生或事件B发生,则称此事件为事件A和事件B的并事件(或和事件),记作 .B A如图:例.若事件K={出现1点或5点} 发生,则事件C1 =
{出现1点}与事件C5 ={出现 5 点 }中至少有一个会
发生,则 二.剖析概念,夯实基础(4)交事件(积事件)若某事件发生当且仅当事件A发生且事件B发生,则称此事件为事件A和事件B的交事件(或积事件)记作 B A如图:例.若事件 M={出现1点且5点}发生,则事件C1 ={出现1点}与事件C5 ={出现5点}同时发生,则 二.剖析概念,夯实基础(5)互斥事件若 为不可能事件( ),那么称事件A与事件B互斥,其含义是:事件A与事件B在任何一次试验中都不会同时发生.AB如图:例.因为事件C1={出现1点}与事件C2={出现2点}
不可能同时发生,故这两个事件互斥.二.剖析概念,夯实基础(6)互为对立事件若 为不可能事件, 为必然事件,那么称事件A与事件B互为对立事件,其含义是:事件A与事件B在任何一次试验中有且仅有一个发生.如图:例. 事件G ={出现的点数为偶数}与事件
H ={出现的点数为奇数} 即为互为对立事件.二.剖析概念,夯实基础①互斥事件可以是两个或两个以上事件的关系,
而对立事件只针对两个事件而言.②从定义上看,两个互斥事件有可能都不发生,也可能有一个发生,也就是不可能同时发生;
而对立事件除了要求这两个事件不同时发生外,还要求这二者之间必须要有一个发生,因此,对立事件是互斥事件,是互斥事件的特殊情况,但互斥事件不一定是对立事件.③从集合角度看,几个事件彼此互斥,是指这几个事件所包含的结果组成的集合的交集为空集;而事件A的对立事件所包含的结果组成的集合是全集中由事件A所包含的结果组成的集合的补集.
互斥事件与对立事件的区别:事件与集合之间的对应关系1.概率P(A)的取值范围(1)0≤P(A)≤1.(2)必然事件的概率是1.(3)不可能事件的概率是0.(4)若A B, 则 P(A) ≤P(B)(二)概率的基本性质二.剖析概念,夯实基础思考:掷一枚骰子,事件C1={出现1点},事件
C3={出现3点}则事件C1 ? C3 发生的频率
与事件C1和事件C3发生的频率之间有什
么关系?结论:当事件A与事件B互斥时
二.剖析概念,夯实基础2.概率的加法公式:如果事件A与事件B互斥,则
P (A ? B)= P (A) + P (B)若事件A,B为对立事件,则
P(B)=1-P(A)3.对立事件的概率公式二.剖析概念,夯实基础注意:1.利用上述公式求概率是,首先要确定
两事件是否互斥,如果没有这一条件,该公式
不能运用.即当两事件不互斥时,应有:如果事件A与事件B互斥,则
P (A ? B)= P (A) + P (B)P (A ? B)= P (A) + P (B) - P(???)2.上述公式可推广,即如果随机事件A1,A2,
……,An中任何两个都是互斥事件,那么有P (A1 ? A2 ?… ?An)= P (A1) + P (A2)+…+P(?n)一般地,在解决比较复杂的事件的概率问题时,常常把复杂事件分解为几个互斥事件,借助该推广公式解决.事件B:命中环数为10环;
事件C:命中环数小于6环.
事件D:命中环数为6、7、8、9、10环
2、从40张扑克牌(红桃、黑桃、方块和梅花点数从1-10各10张)中,任取一张.课中探究1、一个射手进行一次射击:
事件A:命中环数大于7环;例1:试判断下列事件哪些是互斥事件?哪些是对立事件?(1)“抽出红桃”与“抽出黑桃”;
(2)“抽出红色牌”与“抽出黑色牌”;
(3)“抽出点数为5的倍数”与“抽出的点数大于9”;
解:互斥事件有:A和C、B和C、C和D.
对立事件有:C和D.解:互斥事件有:(1)、(2) ;对立事件有:(2)课中探究例2:袋中有12个小球,分别为红球、黑球、黄球、绿球,从中任取一球,得到红球的概率为 ,得到黑球或黄球的概率是 ,得到黄球或绿球的概率也是 ,试求得到黑球、得到黄球、得到绿球的概率各是多少?分析:利用方程的思想及互斥事件、对立事件的概率公式求解 有P(B∪C)=P(B)+P(C)= ;
P(C∪D)=P(C)+P(D)= ;
P(B∪C∪D)=1-P(A)=1- = ,
解得P(B)= ,P(C)= ,P(D)= 解:从袋中任取一球,记事件“摸到红球”、“摸到黑球”、“摸到黄球”、“摸到绿球”为A、B、C、D,则1、事件的关系与运算,区分互斥事件与对立事件小结提升2.概率的基本性质:
1)必然事件概率为1,不可能事件概率为0,因此0≤P(A)≤1;
2)当事件A与B互斥时,满足加法公式:P(A∪B)= P(A)+ P(B);
3)若事件A与B为对立事件,则A∪B为必然事件,所以P(A∪B)= P(A)+ P(B)=1,于是有P(A)=1-P(B);小结提升B反馈检测1、(4)一个人打靶时连续射击两次,事件“至少有一次中靶”的互斥事件是( )
(A)至少有一次中靶.(B)两次都中靶.
(C)只有一次中靶. (D)两次都不中靶.
(5)把红、蓝、黑、白4张纸牌随机分给甲、乙、丙、丁4个人,每人分得一张,事件“甲分得红牌”与事件“乙分得红牌”是( )
(A)对立事件 . (B)互斥但不对立事件.
(C)不可能事件 .( D)以上都不是.
D课本121页B2.抽查10件产品,设事件A:至少有两件次品,则A的对立事件为( )
A. 至多两件次品 B. 至多一件次品
C. 至多两件正品 D. 至少两件正品3.某产品分甲、乙、丙三级,其中乙、丙两级均属次品,若生产中出现乙级品的概率为0.03、丙级品的概率为0.01,则对成品抽查一件抽得正品的概率为( )
A.0.09 B.0.98 C.0.97 D.0.96D4、某射手射击一次射中10环,9环,8环,7环的概率是0.24,0.28,0.19,0.16,计算这名射手射击一次:(1)射中10环或9环的概率;
(2)至少射中7环的概率.(1) P(A∪B)=P(A)+P(B) =0.24+0.28=0.52.(2) 因为它们是互斥事件,所以至少射中7环的概率是0.24+0.28+0.19+0.16=0.875、甲,乙两人下棋,和棋的概率为1/2,乙获胜的概率为1/3,求:(1)甲获胜的概率;(2)甲不输的概率.分析:甲乙两人下棋,其结果有甲胜、和棋、乙胜三种,它们是互斥事件.解:(1)“甲获胜”是“和棋或乙胜”的对立事件,所以甲获胜的概率是P=1-1/2-1/3=1/6.(2)解法1:“甲不输”看作是“甲胜”,“和棋”这两个事件的并事件所以P=1/6+1/2=2/3.
解法2:“甲不输”看作是“乙胜”的对立事件,P=1-1/3=2/3.
