1.1.2 余弦定理 课件

课件19张PPT。1.1.2 余弦定理第一章 解三角形一、复习回顾1.正弦定理及其推论： =2R(R为△ABC外接圆半径）BCAabc思考： 在△ABC中,已知AB=2,BC=5,△ABC的面积为4，
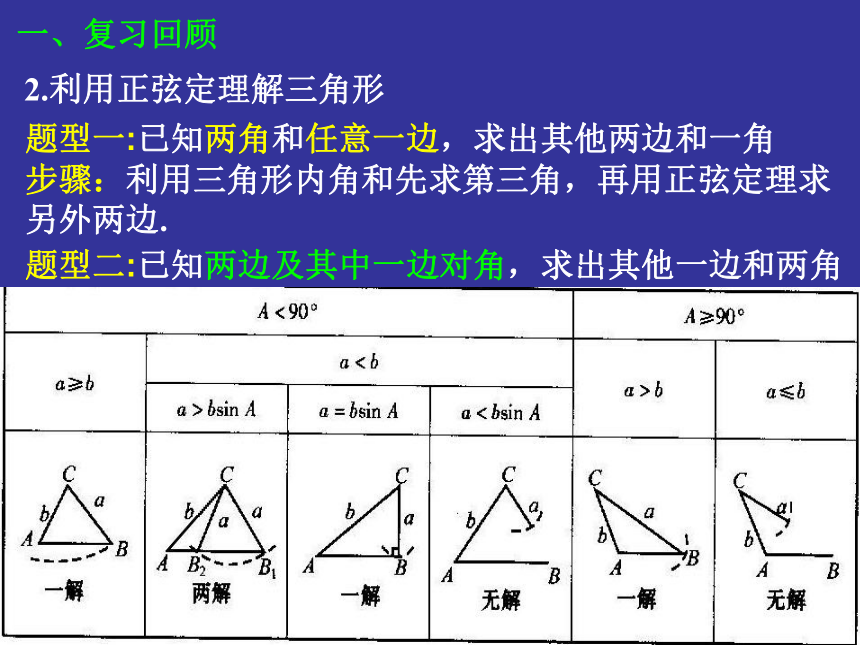
∠ABC=θ，则sinθ= .练习：在△ABC中， ，求此三角形的面积．2.利用正弦定理解三角形题型一:已知两角和任意一边，求出其他两边和一角
步骤：利用三角形内角和先求第三角，再用正弦定理求另外两边.
题型二:已知两边及其中一边对角，求出其他一边和两角一、复习回顾若已知a、b、A的值，则解该三角形的步骤如下：
（1）先利用 求出sinB，从而求出角B；
（2）利用A、B求出角C=180o-(A+B)；
（3）再利用 求出边c.注意：求角B时应注意检验！依条件可知，同理可得二、新课讲解问题：在△ABC中，a=8，b=3，C=60o，求c.如图，在△ABC中，BC=a，AC=b，边BC与AC的夹角为C，试求AB边的长c.题型三:已知三角形的两条边及其夹角,求出另一边。 三角形任何一边的平方等于其他两边的平方和减去
这两边与它们夹角的余弦的积的两倍，即余弦定理：注：利用余弦定理，可以从已知的两边及其夹角求出三角形的第三条边二、新课讲解例3 在△ABC中，已知b=60cm，c=34cm，A=41o，
解该三角形（角度精确到1°，边长精确到1cm）.解：∵a2=b2+c2-2bccosA
=602+342-2×60×34×cos41o≈1676.82
∴a≈41(cm)故由正弦定理可得∵c∴利用计算器可求得 C≈33°
∴B=180o-(A+C) ≈ 180o-(41o+33o)=106°故由余弦定理可得 三、例题讲解 一般地，在“知三边及一角”要求剩下的两个角时，应先求最小的边所对的角.∴利用计算器可求得 C≈33°
∴B=180o-(A+C) ≈ 180o-(41o+33o)=106°
余弦定理的推论：注: 由上述推论, 可以由三角形的三条边求出相应的三个角二、新课讲解例4 在△ABC中，已知a=134.6cm，b=87.8cm，
c=161.7cm，解三角形（角度精确到1′）。解：∴A≈56°20′∴B≈32°53′三、例题讲解利用余弦定理及其推论，可以解决以下两类解三角形的问题：（1）已知两边及其夹角，求其它的边和角；
（2）已知三边，求三个角.练习：在△ABC中
（1）已知a= ，c=2，B=150o，求b；
（2）已知a=2，b= ，c= ，求A.745o二、新课讲解余弦定理及其推论：解三角形的四种基本类型：例5.已知△ABC的三条边长的比为1：2： ，求该
三角形的最大内角.解：依题意可设该三角形三条边分别为则角C为最大内角∴C=120o三、例题讲解又∵0o（2）若A为锐角，则a2 < b2+c2
（3）若A为钝角，则a2 > b2+c2由a2=b2+c2－2bccosA可得利用余弦定理可判断三角形的形状.二、新课讲解钝角三角形2.在锐角三角形三条边的长度分别为2、3、x，试求x的取值范围.变式：若该三角形是钝角三角形呢？AC练习4.在△ABC, ∠B=30o,AB= ,面积S= ,则AC=______.3.在△ABC中，若A=120o，c=5，b=3，则sinBsinC =( )2.△ABC的两边长为2，3，其夹角的余弦为 ，则其外
接圆的半径为( )1.在△ABC中，已知 ，则△ABC中的最小内角的度数是（ ）
A．60o B．45o C．30o D．15oC2 练习在 ⊿ABC中，内角A、B、C对边的边长分别
是 a、b、c已知 c＝2，C＝ ．
（1）若⊿ABC的面积等于 ，求 a、b；
（2）若 ，求 ⊿ABC的面积． 练习在 ⊿ABC中，内角A、B、C对边的边长分别
是 a、b、c已知 c＝2，C＝ ．
（1）若⊿ABC的面积等于 ，求 a、b；
（2）若 ，求 ⊿ABC的面积． 练习在 ⊿ABC中，内角A、B、C对边的边长分别
是 a、b、c已知 c＝2，C＝ ．
（1）若⊿ABC的面积等于 ，求 a、b；
（2）若 ，求 ⊿ABC的面积．四、小结余弦定理及其推论：利用余弦定理判断三角形的形状：
（1）若A为直角，则a2 = b2+c2
（2）若A为锐角，则a2 < b2+c2
（3）若A为钝角，则a2 > b2+c2