1.2 应用举例 课件2
图片预览











文档简介
课件30张PPT。1.2 应用举例[研一题]
[例1]如图,已知在四边形ABCD中,
AD⊥CD,AD=10,AB=14,∠BDA=
60°,∠BCD=135°,求BC的长. [提示] 在△ABD中,利用余弦定理求BD,进而考虑在△BCD中,运用正弦定理求BC. [自主解答] 设BD=x.
在△ABD中,由余弦定理,
得AB2=AD2+BD2-2AD·BDcos∠ADB,
即142=102+x2-2×10xcos 60°,
整理得x2-10x-96=0,
解之得x1=16,x2=-6(舍),
即BD=16.[悟一法]
对于三角形中的长度计算,可直接应用正弦定理或余弦定理解答,而有关四边形中的长度计算问题,一般则需要构造三角形,转化为解三角形问题,这时需分析所求长度与三角形的哪几个要素有关,往往是正弦定理与余弦定理的综合应用.[通一类]
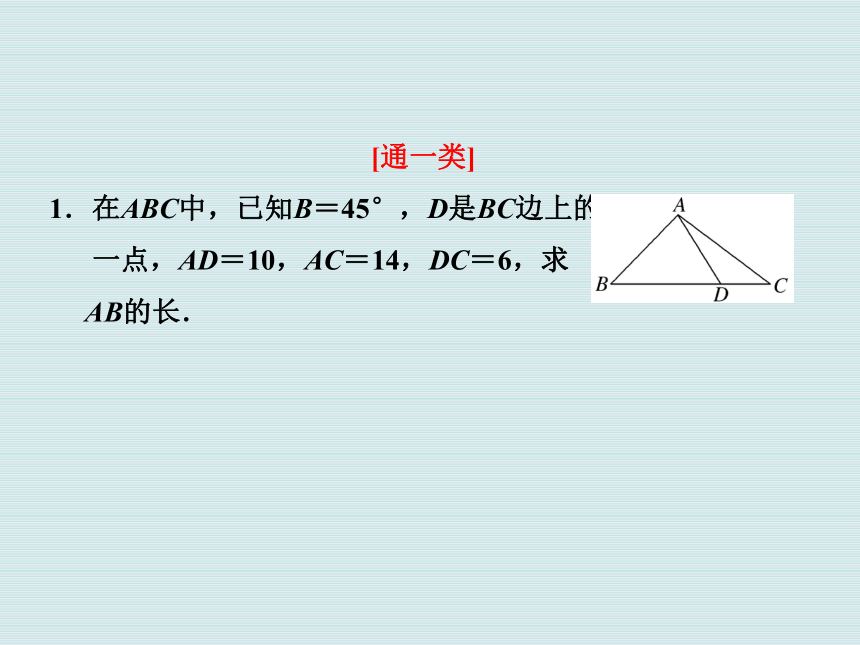
1.在ABC中,已知B=45°,D是BC边上的
一点,AD=10,AC=14,DC=6,求
AB的长.[悟一法]
求三角形的面积,要充分挖掘题目中的条件,转化为求两边及其夹角的正弦问题,要注意方程思想在解题中的应用.[通一类]
3.如图,四边形ABCD中,B=C=120°,
AB=4,BC=CD=2,则该四边形ABCD
的面积.[悟一法]
在三角形几何计算中解决最值问题的关键是引入变量,一般是角,θ,通过正弦定理和余弦定理或其他条件,寻求所需边与θ的关系,从而建立函数关系,转化为三角函数求最值问题加以解决,但求最值时应注意变量θ的取值范围.
[例1]如图,已知在四边形ABCD中,
AD⊥CD,AD=10,AB=14,∠BDA=
60°,∠BCD=135°,求BC的长. [提示] 在△ABD中,利用余弦定理求BD,进而考虑在△BCD中,运用正弦定理求BC. [自主解答] 设BD=x.
在△ABD中,由余弦定理,
得AB2=AD2+BD2-2AD·BDcos∠ADB,
即142=102+x2-2×10xcos 60°,
整理得x2-10x-96=0,
解之得x1=16,x2=-6(舍),
即BD=16.[悟一法]
对于三角形中的长度计算,可直接应用正弦定理或余弦定理解答,而有关四边形中的长度计算问题,一般则需要构造三角形,转化为解三角形问题,这时需分析所求长度与三角形的哪几个要素有关,往往是正弦定理与余弦定理的综合应用.[通一类]
1.在ABC中,已知B=45°,D是BC边上的
一点,AD=10,AC=14,DC=6,求
AB的长.[悟一法]
求三角形的面积,要充分挖掘题目中的条件,转化为求两边及其夹角的正弦问题,要注意方程思想在解题中的应用.[通一类]
3.如图,四边形ABCD中,B=C=120°,
AB=4,BC=CD=2,则该四边形ABCD
的面积.[悟一法]
在三角形几何计算中解决最值问题的关键是引入变量,一般是角,θ,通过正弦定理和余弦定理或其他条件,寻求所需边与θ的关系,从而建立函数关系,转化为三角函数求最值问题加以解决,但求最值时应注意变量θ的取值范围.
