1.2 应用举例 课件3
图片预览








文档简介
课件36张PPT。1.2 应用举例第一课时/正、余弦定理在实际中的应用 新课导入知识探究题型探究达标检测新课导入——实例引领 思维激活实例:李明出校门向南前进200米,再向东走了200米,回到自己家中.
想一想 李明家在学校的哪个方向?能否用角度进一步确定其方位?
(东南方向;能,南偏东45°)知识探究——自主梳理 思考辨析1.仰角和俯角
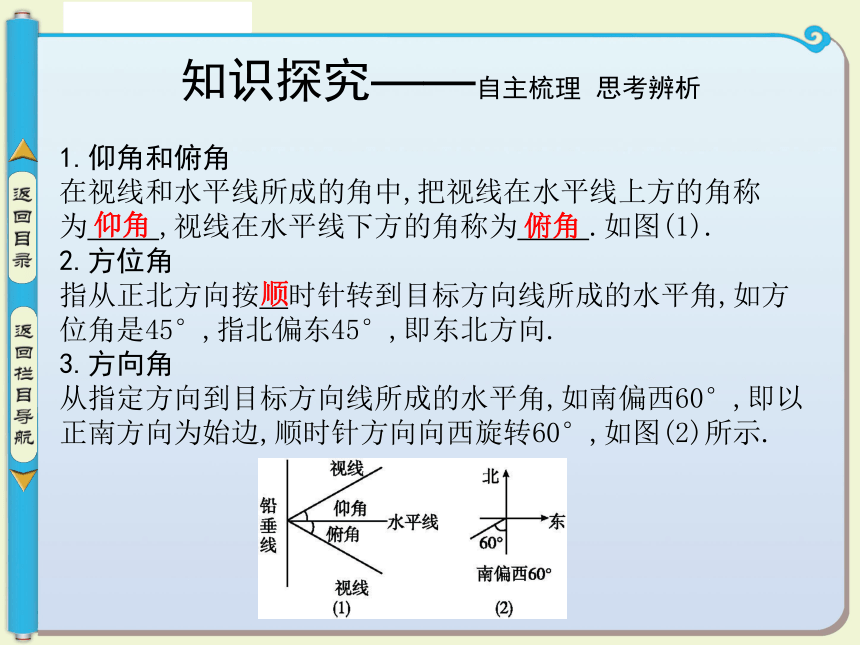
在视线和水平线所成的角中,把视线在水平线上方的角称为 ,视线在水平线下方的角称为 .如图(1).
2.方位角
指从正北方向按 时针转到目标方向线所成的水平角,如方位角是45°,指北偏东45°,即东北方向.
3.方向角
从指定方向到目标方向线所成的水平角,如南偏西60°,即以正南方向为始边,顺时针方向向西旋转60°,如图(2)所示.仰角俯角顺4.基线
在测量上,我们根据测量需要适当确定的线段叫做 .一般来说,基线越长,测量的精确度 .
5.坡度
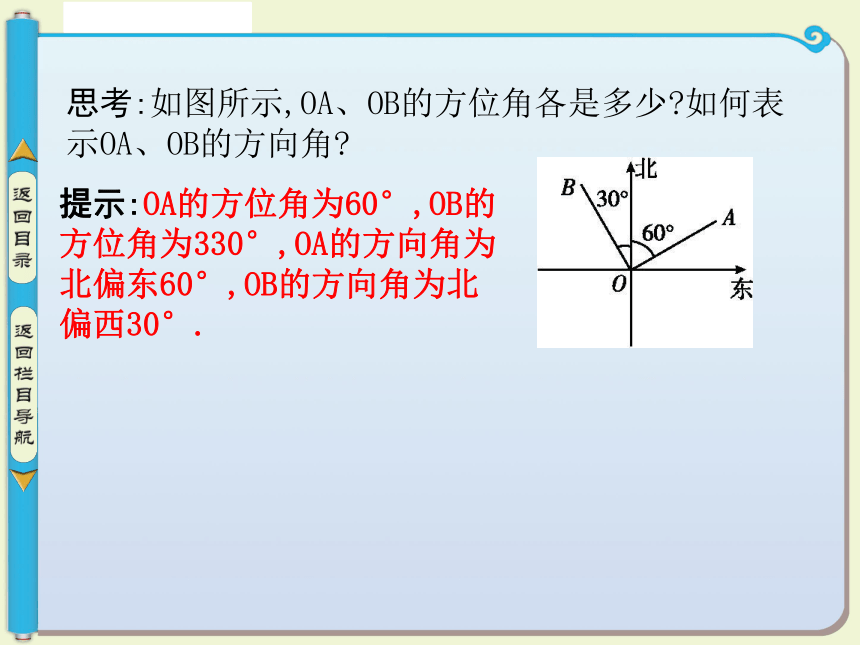
坡面的垂直高度h和水平宽度l的比叫做 (或叫做坡比).基线越高坡度思考:如图所示,OA、OB的方位角各是多少?如何表示OA、OB的方向角? 提示:OA的方位角为60°,OB的方位角为330°,OA的方向角为北偏东60°,OB的方向角为北偏西30°.题型探究——典例剖析 举一反三名师导引:(1)求A、B之间的距离实质就是求线段AB的长度,应把它放在哪个三角形中求解?(可放在△ABC中或△ABD中)
(2)要在△ABC中计算AB,需要知道哪些量?(由于∠ACB=75°已知,因此可求出AC与BC的长度,然后用余弦定理计算)
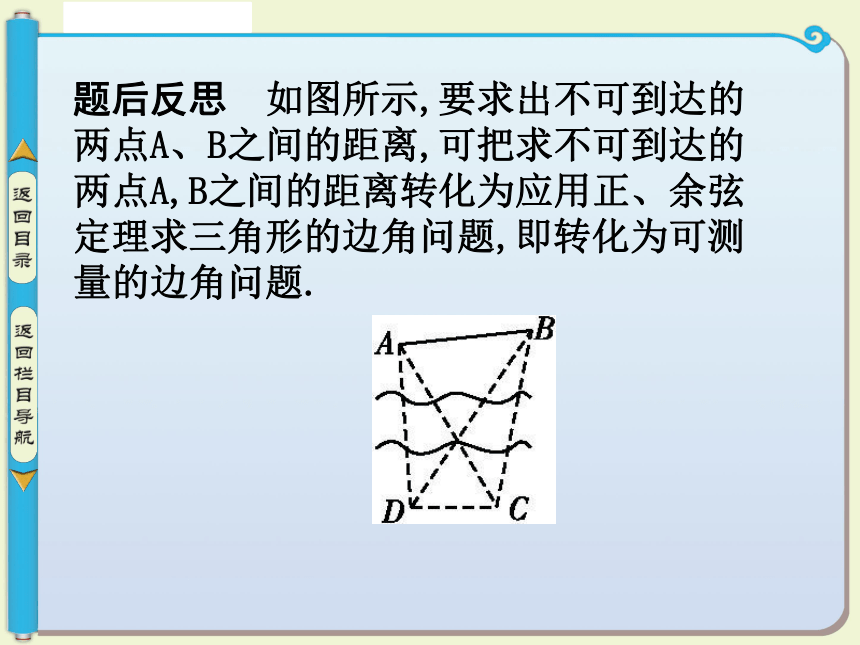
(3)怎样求得AC与BC的长度呢?(可在△ACD中求AC,在△BCD中求BC)题后反思 如图所示,要求出不可到达的两点A、B之间的距离,可把求不可到达的两点A,B之间的距离转化为应用正、余弦定理求三角形的边角问题,即转化为可测量的边角问题.跟踪训练1-1:如图所示,为了计算湖岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两个测量点,现测得AD⊥CD,AD=5 km,AB=7 km,
∠BDA=60°,∠BCD=135°,求两景点B与C的距离.(假设A,B,C,D在同一平面内)答:两景点B与C的距离为4km.题型二 测量高度问题
【例2】 如图,为了测量河对岸的塔高AB,有不同的方案,其中之一是选取与塔底B在同一水平面内的两个测点C和D,测得CD=200米,在C点和D点测得塔顶A的仰角分别是45°和30°,且∠CBD=30°,求塔高AB.(2)在△BCD中,已知CD、∠CBD,又用塔高表示了BC、BD,如何建立关于塔高的方程?(用余弦定理)
(3)怎样求得塔高AB?(解方程,据实际意义得到塔高)题后反思 本题中若无法测得D点看塔顶A的仰角,要得到塔高AB,可再测量∠BCD或∠BDC,这样在△BCD中先用正弦定理求出BC的长度,再在△ACB中求得AB=BC·tan 45°. 跟踪训练2-1:在平地上有A、B两点,A在山的正东,B在山的东南,而且在A的南偏西25°的300米的地方,在A测得山顶的仰角是30°,求山高.(精确到0.1米)答:台风向北偏西45°方向移动.题后反思 测量角度问题也就是通过解三角形求角问题,求角问题可转化为求该角的三角函数值.若是用余弦定理求得该角的余弦,则该角易确定,若用正弦定理求得该角的正弦,则需讨论解的情况.备选例题【例题】 在海岛A上有一座海拔1 km的山峰,山顶设有一个观察站P.有一艘轮船按一固定方向做匀速直线航行,上午11:00时,测得此船在岛北偏东15°、俯角为30°的B处,到11:10时,又测得该船在岛北偏西45°、俯角为60°的C处.求船的航行速度. 达标检测——反馈矫正 及时总结1.从A处望B处的仰角为α,从B处望A处的俯角为β,则α、β的关系为( )
(A)α>β (B)α=β
(C)α+β=90° (D)α+β=180°
解析:根据仰角与俯角的定义知α=β.故选B.BA 3.一船从港口A出发,沿北偏东30°方向行驶了3 km到达B岛,又沿东偏南30°方向行驶了3 km到达C岛,则C岛在港口A的北偏东 方向,距港口A km.?课堂小结
1.测量距离问题:这类问题的情境一般属于“测量有障碍物相隔的两点间的距离”.在测量过程中,要根据实际需要选取合适的基线长度,测量工具要有较高的精确度.
2.测量底部不可到达的建筑物的高度问题.由于底部不可到达,这类问题不能直接用解直角三角形的方法解决,但常用正弦定理和余弦定理,计算出建筑物顶部到一个可到达的点之间的距离,然后转化为解直角三角形的问题.
3.测量角度就是在三角形内利用正弦定理和余弦定理求角的正弦值或余弦值,再根据需要求出所求的角.
想一想 李明家在学校的哪个方向?能否用角度进一步确定其方位?
(东南方向;能,南偏东45°)知识探究——自主梳理 思考辨析1.仰角和俯角
在视线和水平线所成的角中,把视线在水平线上方的角称为 ,视线在水平线下方的角称为 .如图(1).
2.方位角
指从正北方向按 时针转到目标方向线所成的水平角,如方位角是45°,指北偏东45°,即东北方向.
3.方向角
从指定方向到目标方向线所成的水平角,如南偏西60°,即以正南方向为始边,顺时针方向向西旋转60°,如图(2)所示.仰角俯角顺4.基线
在测量上,我们根据测量需要适当确定的线段叫做 .一般来说,基线越长,测量的精确度 .
5.坡度
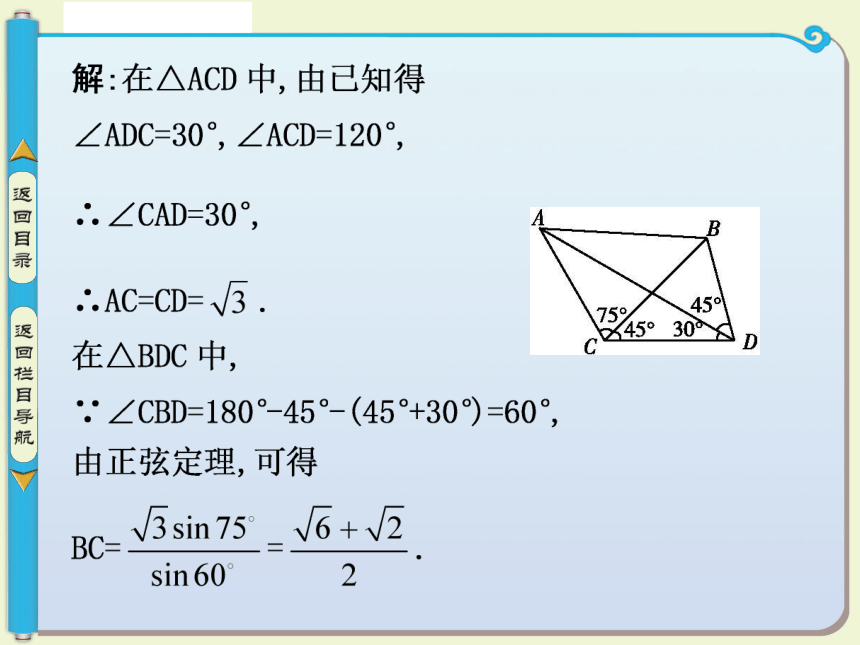
坡面的垂直高度h和水平宽度l的比叫做 (或叫做坡比).基线越高坡度思考:如图所示,OA、OB的方位角各是多少?如何表示OA、OB的方向角? 提示:OA的方位角为60°,OB的方位角为330°,OA的方向角为北偏东60°,OB的方向角为北偏西30°.题型探究——典例剖析 举一反三名师导引:(1)求A、B之间的距离实质就是求线段AB的长度,应把它放在哪个三角形中求解?(可放在△ABC中或△ABD中)
(2)要在△ABC中计算AB,需要知道哪些量?(由于∠ACB=75°已知,因此可求出AC与BC的长度,然后用余弦定理计算)
(3)怎样求得AC与BC的长度呢?(可在△ACD中求AC,在△BCD中求BC)题后反思 如图所示,要求出不可到达的两点A、B之间的距离,可把求不可到达的两点A,B之间的距离转化为应用正、余弦定理求三角形的边角问题,即转化为可测量的边角问题.跟踪训练1-1:如图所示,为了计算湖岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两个测量点,现测得AD⊥CD,AD=5 km,AB=7 km,
∠BDA=60°,∠BCD=135°,求两景点B与C的距离.(假设A,B,C,D在同一平面内)答:两景点B与C的距离为4km.题型二 测量高度问题
【例2】 如图,为了测量河对岸的塔高AB,有不同的方案,其中之一是选取与塔底B在同一水平面内的两个测点C和D,测得CD=200米,在C点和D点测得塔顶A的仰角分别是45°和30°,且∠CBD=30°,求塔高AB.(2)在△BCD中,已知CD、∠CBD,又用塔高表示了BC、BD,如何建立关于塔高的方程?(用余弦定理)
(3)怎样求得塔高AB?(解方程,据实际意义得到塔高)题后反思 本题中若无法测得D点看塔顶A的仰角,要得到塔高AB,可再测量∠BCD或∠BDC,这样在△BCD中先用正弦定理求出BC的长度,再在△ACB中求得AB=BC·tan 45°. 跟踪训练2-1:在平地上有A、B两点,A在山的正东,B在山的东南,而且在A的南偏西25°的300米的地方,在A测得山顶的仰角是30°,求山高.(精确到0.1米)答:台风向北偏西45°方向移动.题后反思 测量角度问题也就是通过解三角形求角问题,求角问题可转化为求该角的三角函数值.若是用余弦定理求得该角的余弦,则该角易确定,若用正弦定理求得该角的正弦,则需讨论解的情况.备选例题【例题】 在海岛A上有一座海拔1 km的山峰,山顶设有一个观察站P.有一艘轮船按一固定方向做匀速直线航行,上午11:00时,测得此船在岛北偏东15°、俯角为30°的B处,到11:10时,又测得该船在岛北偏西45°、俯角为60°的C处.求船的航行速度. 达标检测——反馈矫正 及时总结1.从A处望B处的仰角为α,从B处望A处的俯角为β,则α、β的关系为( )
(A)α>β (B)α=β
(C)α+β=90° (D)α+β=180°
解析:根据仰角与俯角的定义知α=β.故选B.BA 3.一船从港口A出发,沿北偏东30°方向行驶了3 km到达B岛,又沿东偏南30°方向行驶了3 km到达C岛,则C岛在港口A的北偏东 方向,距港口A km.?课堂小结
1.测量距离问题:这类问题的情境一般属于“测量有障碍物相隔的两点间的距离”.在测量过程中,要根据实际需要选取合适的基线长度,测量工具要有较高的精确度.
2.测量底部不可到达的建筑物的高度问题.由于底部不可到达,这类问题不能直接用解直角三角形的方法解决,但常用正弦定理和余弦定理,计算出建筑物顶部到一个可到达的点之间的距离,然后转化为解直角三角形的问题.
3.测量角度就是在三角形内利用正弦定理和余弦定理求角的正弦值或余弦值,再根据需要求出所求的角.
