1.2 应用举例 课件4

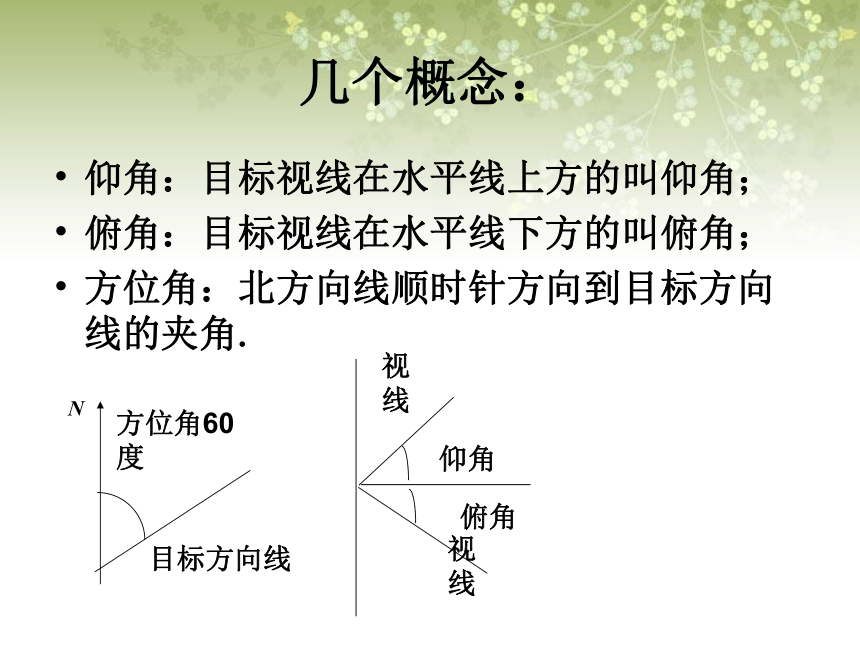
课件18张PPT。1.2 应用实例（其中：R为△ABC的外接圆半径）复习回顾 2、余弦定理：变形1、正弦定理：几个概念：仰角：目标视线在水平线上方的叫仰角；
俯角：目标视线在水平线下方的叫俯角；
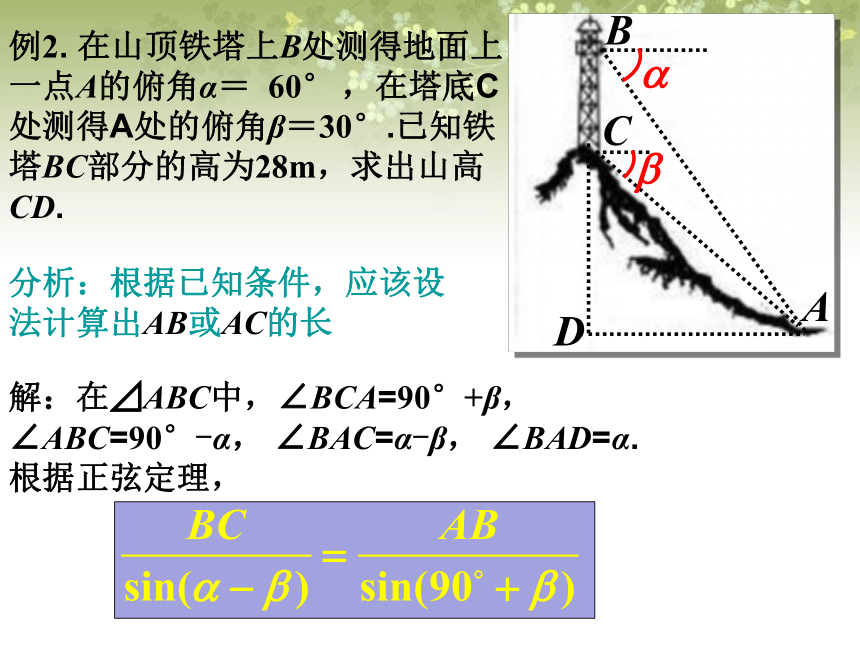
方位角：北方向线顺时针方向到目标方向线的夹角.N目标方向线方位角60度俯角视线仰角视线在△ABC中，边BC，CA，AB上的高分别为 ，那么它们如何用已知边和角来表示呢?根据三角形面积公式 ，和以上公式可推导出如下面积公式：正弦定理和余弦定理在实际测量中有许多应用：定理应用例1.如图为了测量河对岸两点A，B之间的距离，在河岸这边取C，D，测得∠BDC=60°，∠ACD=47°，∠BCD=72°，∠ADC=85°，，CD=100m，设A，B，C，D在同一平面内，试求A，B之间的距离?解：例2. 在山顶铁塔上B处测得地面上一点A的俯角α＝ 60° ，在塔底C处测得A处的俯角β＝30°.已知铁塔BC部分的高为28m，求出山高CD.分析：根据已知条件，应该设法计算出AB或AC的长解：在⊿ABC中，∠BCA=90°+β， ∠ABC=90°-α， ∠BAC=α-β， ∠BAD=α.根据正弦定理，CD=BD-BC=42-28=14(m)答：山的高度约为14米.例3.在△ABC中，根据下列条件，求三角形的面积S(精确到0.1cm2). (1)已知a =14.8cm，c =23.5 cm ，B =148.5°；解：(2)已知B=62.7°，C =65.8°，b=3.16cm；解：（3）已知三边的长分别为a=41.4cm，b=27.3cm，c=38.7cm.解： 例4. 在△ABC 中，求证：
（1）（2）分析：这是一道关于三角形边角关系恒等
式的证明问题，观察式子左右两边的特点，联
想到用正弦定理来证明.显然 k≠0，所以证明：（1）根据正弦定理，可设（2）根据余弦定理的推论，右边==左边解题关键：
利用正弦定理或余弦定理将已知条件转化为只含边的式子或只含角的三角函数式，然后化简并考察边或角的关系，从而确定三角形的形状.特别是有些条件既可用正弦定理也可用余弦定理甚至可以两者混用.1、分析题意，弄清已知和所求；
2、根据题意，画出示意图；
3、将实际问题转化为数学问题，写出已知所求；
4、正确运用正、余弦定理.求解三角形应用题的一般步骤：课堂小结实际问题抽象概括示意图数学模型推理演算数学模型的解实际问题的解还原说明课堂小结三角形面积公式：谢谢观看！