1.1.1 正弦定理 课件3
图片预览










文档简介
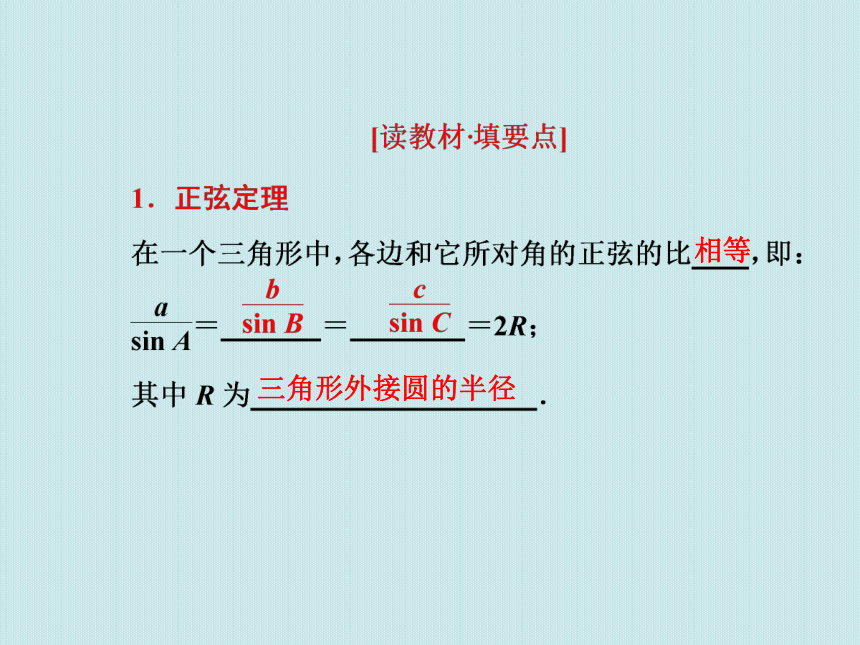
课件35张PPT。1.1.1 正弦定理相等三角形外接圆的半径[小问题·大思维]
1.正弦定理对于任意的三角形都成立吗?
提示:都成立.
2.在△ABC中,角A,B,C的对边分别为a,b,c,那么
a∶b∶c=A∶B∶C对吗?
提示:不对.根据正弦定理,a=2Rsin A,b=2Rsin B,c=2Rsin C.所以a∶b∶c=sin A∶sin B∶sin C. [提示] (1)由三角形内角和定理可求得C,进而运用正弦定理求a,b.
(2)先运用正弦定理求sin A,再用三角形的性质“大边对大角”确定角A,进而用三角形的内角和定理和正弦定理求B,b.[悟一法]
1.把三角形的三个角和它们的对边叫作三角形的元素,已知三角形的几个元素求其他元素的过程,叫做解三角形.
2.应用正弦定理可解两类三角形
(1)已知两角和任意一边,求第三个角和另外两边;
(2)已知两边和其中一边的对角,求第三边和另外两角.
其中类型(1)只有一解,类型(2)可能有两解、一解或无解. 3.已知两边及其中一边的对角,判断三角形解的个数的方法
方法一:应用三角形中大边对大角的性质以及正弦函数的值域判断解的个数.
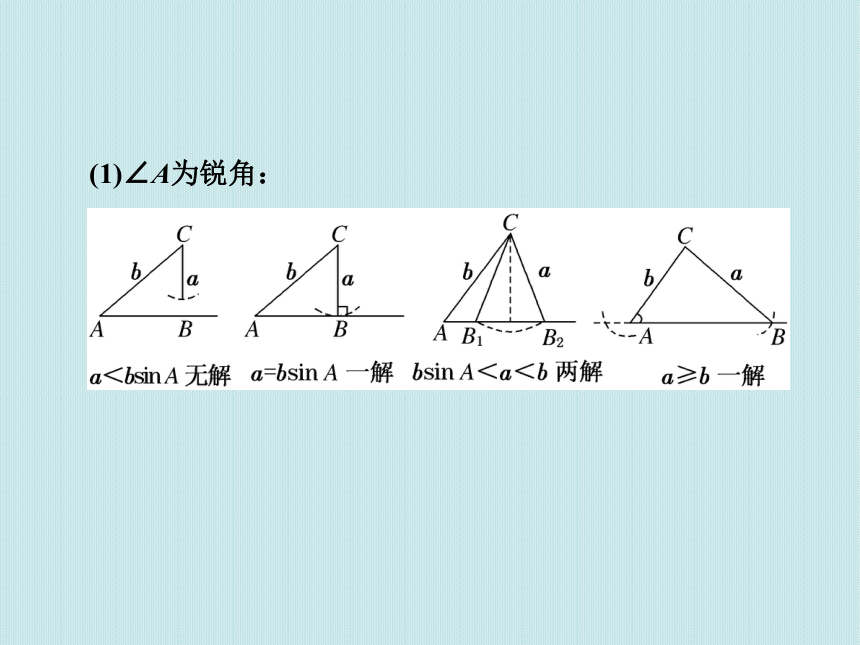
方法二:在△ABC中,已知a、b和∠A,以点C为圆心,以边长a为半径画弧,此弧与除去顶点A的射线AB的公共点的个数即为三角形的个数,如图,解的个数见下表:(1)∠A为锐角:(2)∠A为直角或钝角:[研一题]
[例2] 已知△ABC中,bsin B=csin C,且sin2 A=sin2B+sin2C,试判断三角形的形状.
[提示] 利用正弦定理的变形(如a=2Rsin A),将条件中的角化为边,或将边化为角,从而进行判断.[悟一法]
1.判断三角形的形状,可以从考察三边的关系入手,也可以从三个内角的关系入手,从条件出发,利用正弦定理进行代换、转化,呈现出边与边的关系,或角与角的关系,从而进行判断.
2.判断三角形的形状,主要看其是否是正三角形,等腰三角形、直角三角形、钝角三角形、锐角三角形等,要特别注意“等腰直角三角形”与“等腰或直角三角形”的区别.[通一类]
2.[例题多维思考] 若将本题条件中“bsin B=csin C”改为
“sin A=2sin Bcos C”,其他不变,结果如何?
1.正弦定理对于任意的三角形都成立吗?
提示:都成立.
2.在△ABC中,角A,B,C的对边分别为a,b,c,那么
a∶b∶c=A∶B∶C对吗?
提示:不对.根据正弦定理,a=2Rsin A,b=2Rsin B,c=2Rsin C.所以a∶b∶c=sin A∶sin B∶sin C. [提示] (1)由三角形内角和定理可求得C,进而运用正弦定理求a,b.
(2)先运用正弦定理求sin A,再用三角形的性质“大边对大角”确定角A,进而用三角形的内角和定理和正弦定理求B,b.[悟一法]
1.把三角形的三个角和它们的对边叫作三角形的元素,已知三角形的几个元素求其他元素的过程,叫做解三角形.
2.应用正弦定理可解两类三角形
(1)已知两角和任意一边,求第三个角和另外两边;
(2)已知两边和其中一边的对角,求第三边和另外两角.
其中类型(1)只有一解,类型(2)可能有两解、一解或无解. 3.已知两边及其中一边的对角,判断三角形解的个数的方法
方法一:应用三角形中大边对大角的性质以及正弦函数的值域判断解的个数.
方法二:在△ABC中,已知a、b和∠A,以点C为圆心,以边长a为半径画弧,此弧与除去顶点A的射线AB的公共点的个数即为三角形的个数,如图,解的个数见下表:(1)∠A为锐角:(2)∠A为直角或钝角:[研一题]
[例2] 已知△ABC中,bsin B=csin C,且sin2 A=sin2B+sin2C,试判断三角形的形状.
[提示] 利用正弦定理的变形(如a=2Rsin A),将条件中的角化为边,或将边化为角,从而进行判断.[悟一法]
1.判断三角形的形状,可以从考察三边的关系入手,也可以从三个内角的关系入手,从条件出发,利用正弦定理进行代换、转化,呈现出边与边的关系,或角与角的关系,从而进行判断.
2.判断三角形的形状,主要看其是否是正三角形,等腰三角形、直角三角形、钝角三角形、锐角三角形等,要特别注意“等腰直角三角形”与“等腰或直角三角形”的区别.[通一类]
2.[例题多维思考] 若将本题条件中“bsin B=csin C”改为
“sin A=2sin Bcos C”,其他不变,结果如何?
