1.3 探究与发现—解斜三角形的应用举例 学案5(无答案)
文档属性
| 名称 | 1.3 探究与发现—解斜三角形的应用举例 学案5(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 119.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-06 00:00:00 | ||
图片预览

文档简介
1.2
解斜三角形的应用举例
学案
学习目标
能够运用正弦定理、余弦定理等知识和方法解决一些有关计算角度的实际问题
培养学生提出问题、正确分析问题、独立解决问题的能力,并在学习过程中激发学生的探索精神。
重点、难点
能根据正弦定理、余弦定理的特点找到已知条件和所求角的关系;灵活运用正弦定理和余弦定理解关于角度的问题。
自主学习
Ⅰ.
[创设情境]
在浩瀚无垠的海面上如何确保轮船不迷失方向,保持一定的航速和航向呢?今天我们接着探讨这方面的测量问题。
Ⅱ.合作探究
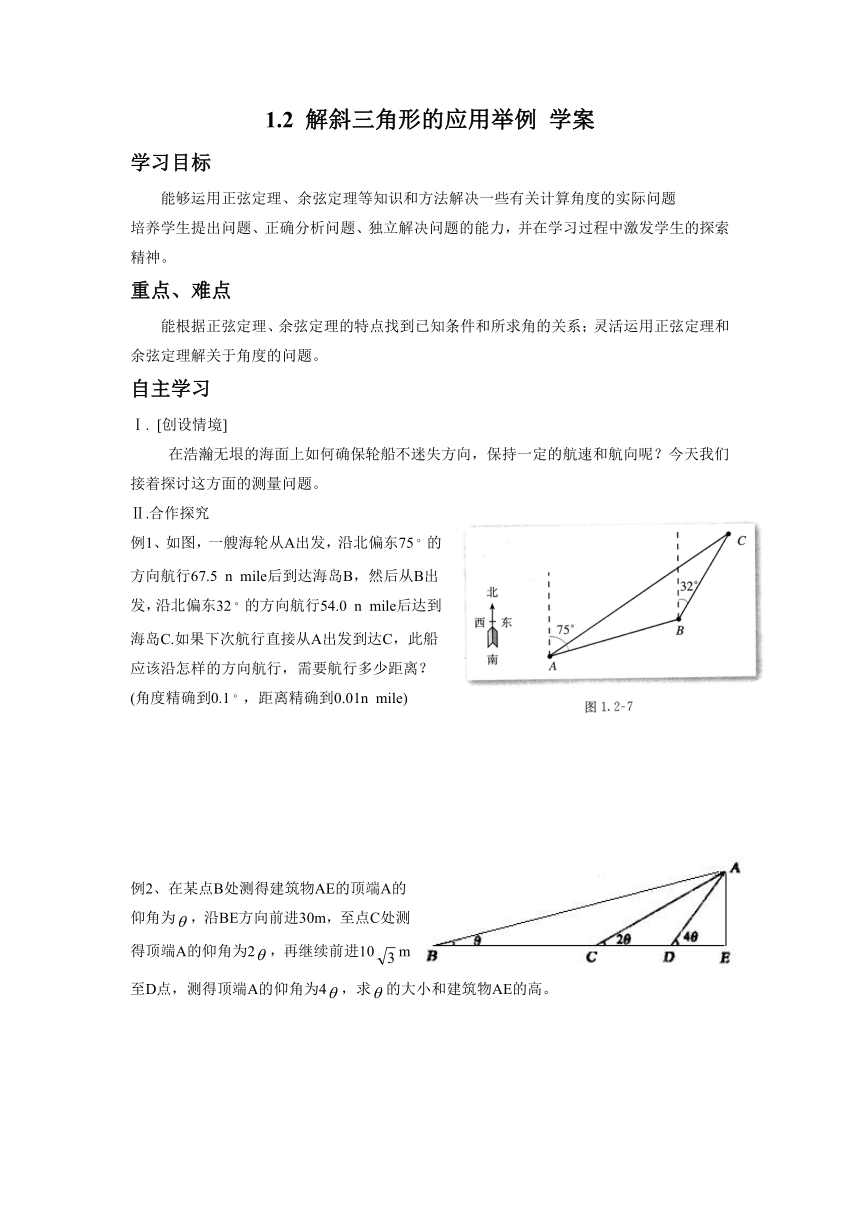
例1、如图,一艘海轮从A出发,沿北偏东75的方向航行67.5
n
mile后到达海岛B,然后从B出发,沿北偏东32的方向航行54.0
n
mile后达到海岛C.如果下次航行直接从A出发到达C,此船应该沿怎样的方向航行,需要航行多少距离?(角度精确到0.1,距离精确到0.01n
mile)
例2、在某点B处测得建筑物AE的顶端A的仰角为,沿BE方向前进30m,至点C处测得顶端A的仰角为2,再继续前进10m至D点,测得顶端A的仰角为4,求的大小和建筑物AE的高。
课堂检测
1、某巡逻艇在A处发现北偏东45相距9海里的C处有一艘走私船,正沿南偏东75的方向以10海里/小时的速度向我海岸行驶,巡逻艇立即以14海里/小时的速度沿着直线方向追去,问巡逻艇应该沿什么方向去追?需要多少时间才追赶上该走私船?()
2、如图,一架飞机原计划从空中A处直飞相距680
km的空间B处,为避开直飞途中的雷雨云层,飞机在A处沿与原飞行方向成θ角的方向直飞,在中途C处转向与原方向成45°角的方向直飞到达B处,已知sin
θ=.
(1)求tan
C;
(2)求新的飞行路程比原飞行路程多多少
km(取≈1.414)
解斜三角形的应用举例
学案
学习目标
能够运用正弦定理、余弦定理等知识和方法解决一些有关计算角度的实际问题
培养学生提出问题、正确分析问题、独立解决问题的能力,并在学习过程中激发学生的探索精神。
重点、难点
能根据正弦定理、余弦定理的特点找到已知条件和所求角的关系;灵活运用正弦定理和余弦定理解关于角度的问题。
自主学习
Ⅰ.
[创设情境]
在浩瀚无垠的海面上如何确保轮船不迷失方向,保持一定的航速和航向呢?今天我们接着探讨这方面的测量问题。
Ⅱ.合作探究
例1、如图,一艘海轮从A出发,沿北偏东75的方向航行67.5
n
mile后到达海岛B,然后从B出发,沿北偏东32的方向航行54.0
n
mile后达到海岛C.如果下次航行直接从A出发到达C,此船应该沿怎样的方向航行,需要航行多少距离?(角度精确到0.1,距离精确到0.01n
mile)
例2、在某点B处测得建筑物AE的顶端A的仰角为,沿BE方向前进30m,至点C处测得顶端A的仰角为2,再继续前进10m至D点,测得顶端A的仰角为4,求的大小和建筑物AE的高。
课堂检测
1、某巡逻艇在A处发现北偏东45相距9海里的C处有一艘走私船,正沿南偏东75的方向以10海里/小时的速度向我海岸行驶,巡逻艇立即以14海里/小时的速度沿着直线方向追去,问巡逻艇应该沿什么方向去追?需要多少时间才追赶上该走私船?()
2、如图,一架飞机原计划从空中A处直飞相距680
km的空间B处,为避开直飞途中的雷雨云层,飞机在A处沿与原飞行方向成θ角的方向直飞,在中途C处转向与原方向成45°角的方向直飞到达B处,已知sin
θ=.
(1)求tan
C;
(2)求新的飞行路程比原飞行路程多多少
km(取≈1.414)
