福建省福州文博中学2016-2017学年高一上学期期中考试数学试题
文档属性
| 名称 | 福建省福州文博中学2016-2017学年高一上学期期中考试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 195.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-06 19:56:29 | ||
图片预览




文档简介
福州文博中学2016-2017学年第一学期
高一年级期中考数学科考试(题目卷)
(完卷时间:120分钟,总分150分)
一、选择题:(本大题共12小题,每小题5
( http: / / www.21cnjy.com )分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案的序号填在答题纸上.)
1.下列关系正确的是(
)
A.
B.
C.
D.
2.下列四组函数中,相等的两个函数是(
)
A.
B.
C.,
D.
3.函数的定义域为(
)
A.
(,+∞)
B.(
,1
C.[1,+∞
D.
4.已知幂函数的图象经过点,则的值为(
)
A.
B. 16 C.2
D.
5.下列函数中,既是奇函数又在区间上单调递增的函数为(
)
A
B
C
D
6.下列大小关系正确的是(
)
A
B
C
D
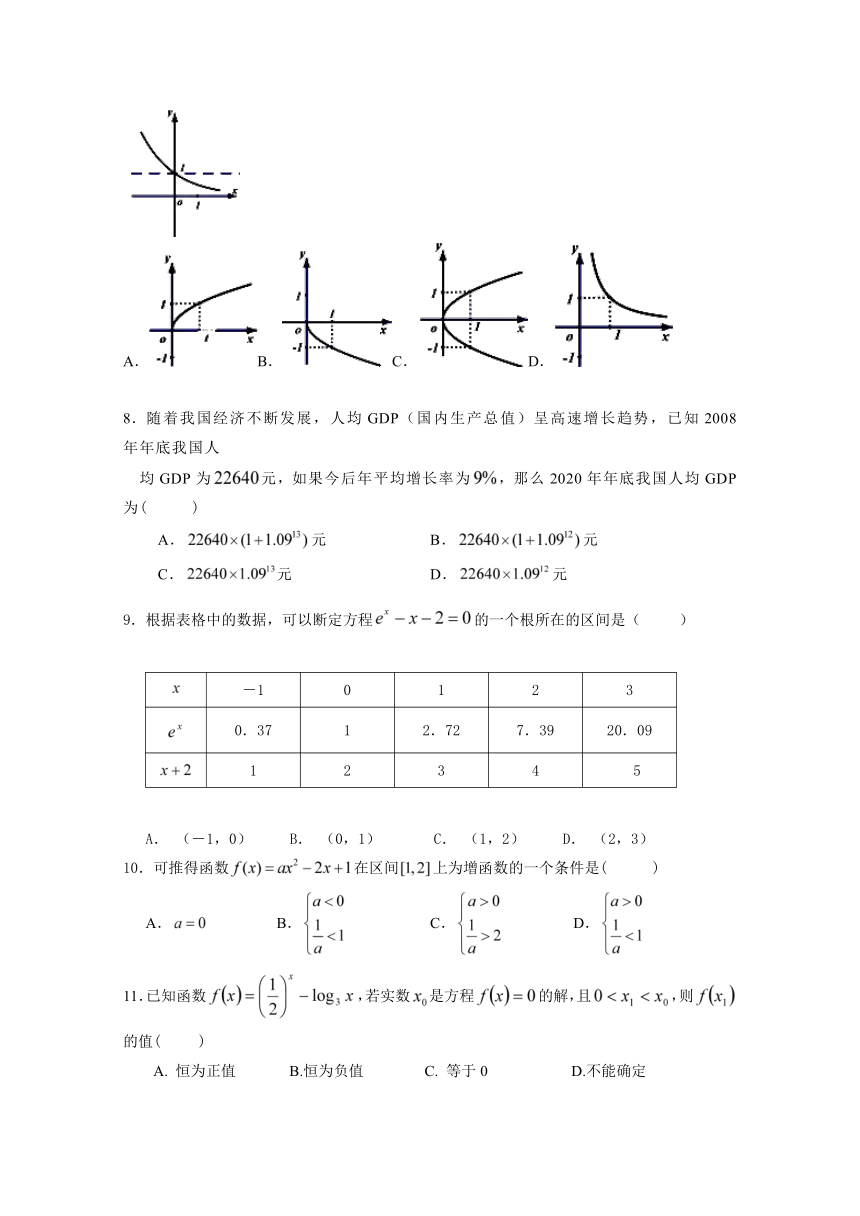
7.若函数(,且)的图象如图,其中为常数.则函数的大致图象是(
)
( http: / / www.21cnjy.com )
A.
( http: / / www.21cnjy.com )B.
( http: / / www.21cnjy.com )C.
( http: / / www.21cnjy.com )D.
( http: / / www.21cnjy.com )
8.随着我国经济不断发展,人均GDP(国内生产总值)呈高速增长趋势,已知2008年年底我国人
均GDP为元,如果今后年平均增长率为,那么2020年年底我国人均GDP为(
)
A.元
B.元
C.元
D.元
9.根据表格中的数据,可以断定方程的一个根所在的区间是(
)
-1
0
1
2
3
0.37
1
2.72
7.39
20.09
1
2
3
4
5
A.
(-1,0)
B.
(0,1)
C.
(1,2)
D.
(2,3)
10.可推得函数在区间上为增函数的一个条件是(
)
A.
B.
C.
D.
11.已知函数,若实数是方程的解,且,则的值(
)
A.
恒为正值
B.恒为负值
C.
等于0
D.不能确定
12.定义在上的偶函数,当时,且为增函数,给出下列四个结论:
①在上单调递增;
②当时,有;
③在上单调递减;
④
在上单调递减.
其中正确的结论是(
)
A.①③
B.②③
C.②④
D.③④
二、填空题:(本大题共4小题,每小题5分,共20分。在答题卡上的相应题目的答题区域内作答)
13.已知集合,则该集合的真子集个数为
14.
已知函数,则=
15.已知函数,若函数有个零点,则实数的取值范围
16.下列几个命题
①方程的有一个正实根,一个负实根,则;
②函数是偶函数,但不是奇函数;
③函数的值域是,则函数的值域为;
④一条曲线和直线的公共点个数是,则的值不可能是1。
其中正确的有___________________
三、解答题(本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分10分)计算下列各小题的值:
(1)
计算:
(2)
解关于的方程:.
18.(本小题满分12分)
已知集合,,.
(1)求,;(2)若,求实数的取值范围.
19.(本小题满分12分)
已知是定义在上的奇函数,当时,。
(1)
如图所示已画出在轴右侧的图象,请补全函数完整的图象;
(2)求函数的表达式;
(3)写出函数的单调区间(不需要证明).
20.(本小题满分12分)
某商场销售某种商品的经验表明,该商品每日的销售量(单位:千克)与销售价格(单位:元/千克)满足关系式:,其中,为常数。已知销售价格为元/千克时,每日可售出该商品千克。
(1)求的值;
(2)若该商品的成本为元/千克,试确定销售价格的值,使商场每日销售该商品所获得的利润最大。
21.(本小题满分12分)
已知二次函数为常数,且)满足条件:,且方程有两个相等的实数根。(1)求的解析式;(2)求在上的最大值。
22.(本小题满分12分)
对于函数(且)
(Ⅰ)判断函数的奇偶性;
(Ⅱ)探究函数的单调区间,并给予证明;
(Ⅲ)当时,求函数在上的最大值和最小值.
福州文博中学2016-2017学年第一学期
高一年级期中考数学科考试(答案卷)
(完卷时间:120分钟,总分:150分)
题号
一
二
17
18
19
20
21
22
总分
得分
评卷教师
一、选择题:(本题共12小题,每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
B
D
C
C
A
D
C
D
A
B
二、填空题:(本题共4小题,每小题5分,共20分)
13.
.
14
15.
.
16.
①④
三、解答题:(本题共6小题,共70分)
17.(本题10分)
计算:
………………………………………3分
………………………………………5分
解关于的方程:
………………………………………8分
经检验得
………………………………………10分
18.(本题12分)
解:(1),,
∴或,又,……………………4分
∴;………………………6分
(2)若,则需
,解得,
…………………10分
故实数的取值范围为.…………………………………………………12分
19.(本题12分)
(1)略
---------
4分
(2)由图像可得,,
-------
6分
当时,由图像或利用奇函数可得
8分
---------
9分
(3)单调递增区间:,
单调递减区间………………12分
20.
(本题12分)
解:(1)因为时,,由函数式 得 ,
所以.--------------------4分
(2)因为,所以该商品每日的销售量为,.
每日销售该商品所获得的利润为,.----7分
当时
21.(本题12分)
解:(1)∵方程有两等根,即有两等根,
∴,解得; ………………………………………2分
∵,得,……………………………4分
∴是函数图象的对称轴,而此函数图象的对称轴是直线,
∴,∴,故.
……………………………6分
(2)∵函数的图象的对称轴为,,
∴当时,在上是增函数,∴,………………………8分
当时,在上是增函数,在上是减函数,∴,…10分
综上,.……………………………12分
22.解:(Ⅰ)由得
∴ 函数的定义域为,关于原点对称 ……………1分
∵ ………………………………………2分
∴ ………………3分
∴ 函数为奇函数 ……………………………………………………4分
(Ⅱ)任取,且,则
………………………5分
∵
⑴ 当时,
∴
∴ ,即
∴ 在为增函数 ……………………………………………6分
⑵ 当时,
∴
∴ ,即
∴ 在为减函数 ……………………………………………8分
由(Ⅰ)知,函数为奇函数,其图象关于原点对称
∴ 当时,函数的递增区间为和;当时,函数的递减
区间为和. ……………………………………………9分
(Ⅲ)由(Ⅱ)可知,当时,函数在区间和均上为减函数,则
当时,
………………………………………………………………………………………10分
当时,
………………………………………………………………………………………11分
∴ 函数在上的
最大值为,最小值为.
……………………………………………………………………………………12分
得分
高一年级期中考数学科考试(题目卷)
(完卷时间:120分钟,总分150分)
一、选择题:(本大题共12小题,每小题5
( http: / / www.21cnjy.com )分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案的序号填在答题纸上.)
1.下列关系正确的是(
)
A.
B.
C.
D.
2.下列四组函数中,相等的两个函数是(
)
A.
B.
C.,
D.
3.函数的定义域为(
)
A.
(,+∞)
B.(
,1
C.[1,+∞
D.
4.已知幂函数的图象经过点,则的值为(
)
A.
B. 16 C.2
D.
5.下列函数中,既是奇函数又在区间上单调递增的函数为(
)
A
B
C
D
6.下列大小关系正确的是(
)
A
B
C
D
7.若函数(,且)的图象如图,其中为常数.则函数的大致图象是(
)
( http: / / www.21cnjy.com )
A.
( http: / / www.21cnjy.com )B.
( http: / / www.21cnjy.com )C.
( http: / / www.21cnjy.com )D.
( http: / / www.21cnjy.com )
8.随着我国经济不断发展,人均GDP(国内生产总值)呈高速增长趋势,已知2008年年底我国人
均GDP为元,如果今后年平均增长率为,那么2020年年底我国人均GDP为(
)
A.元
B.元
C.元
D.元
9.根据表格中的数据,可以断定方程的一个根所在的区间是(
)
-1
0
1
2
3
0.37
1
2.72
7.39
20.09
1
2
3
4
5
A.
(-1,0)
B.
(0,1)
C.
(1,2)
D.
(2,3)
10.可推得函数在区间上为增函数的一个条件是(
)
A.
B.
C.
D.
11.已知函数,若实数是方程的解,且,则的值(
)
A.
恒为正值
B.恒为负值
C.
等于0
D.不能确定
12.定义在上的偶函数,当时,且为增函数,给出下列四个结论:
①在上单调递增;
②当时,有;
③在上单调递减;
④
在上单调递减.
其中正确的结论是(
)
A.①③
B.②③
C.②④
D.③④
二、填空题:(本大题共4小题,每小题5分,共20分。在答题卡上的相应题目的答题区域内作答)
13.已知集合,则该集合的真子集个数为
14.
已知函数,则=
15.已知函数,若函数有个零点,则实数的取值范围
16.下列几个命题
①方程的有一个正实根,一个负实根,则;
②函数是偶函数,但不是奇函数;
③函数的值域是,则函数的值域为;
④一条曲线和直线的公共点个数是,则的值不可能是1。
其中正确的有___________________
三、解答题(本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分10分)计算下列各小题的值:
(1)
计算:
(2)
解关于的方程:.
18.(本小题满分12分)
已知集合,,.
(1)求,;(2)若,求实数的取值范围.
19.(本小题满分12分)
已知是定义在上的奇函数,当时,。
(1)
如图所示已画出在轴右侧的图象,请补全函数完整的图象;
(2)求函数的表达式;
(3)写出函数的单调区间(不需要证明).
20.(本小题满分12分)
某商场销售某种商品的经验表明,该商品每日的销售量(单位:千克)与销售价格(单位:元/千克)满足关系式:,其中,为常数。已知销售价格为元/千克时,每日可售出该商品千克。
(1)求的值;
(2)若该商品的成本为元/千克,试确定销售价格的值,使商场每日销售该商品所获得的利润最大。
21.(本小题满分12分)
已知二次函数为常数,且)满足条件:,且方程有两个相等的实数根。(1)求的解析式;(2)求在上的最大值。
22.(本小题满分12分)
对于函数(且)
(Ⅰ)判断函数的奇偶性;
(Ⅱ)探究函数的单调区间,并给予证明;
(Ⅲ)当时,求函数在上的最大值和最小值.
福州文博中学2016-2017学年第一学期
高一年级期中考数学科考试(答案卷)
(完卷时间:120分钟,总分:150分)
题号
一
二
17
18
19
20
21
22
总分
得分
评卷教师
一、选择题:(本题共12小题,每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
B
D
C
C
A
D
C
D
A
B
二、填空题:(本题共4小题,每小题5分,共20分)
13.
.
14
15.
.
16.
①④
三、解答题:(本题共6小题,共70分)
17.(本题10分)
计算:
………………………………………3分
………………………………………5分
解关于的方程:
………………………………………8分
经检验得
………………………………………10分
18.(本题12分)
解:(1),,
∴或,又,……………………4分
∴;………………………6分
(2)若,则需
,解得,
…………………10分
故实数的取值范围为.…………………………………………………12分
19.(本题12分)
(1)略
---------
4分
(2)由图像可得,,
-------
6分
当时,由图像或利用奇函数可得
8分
---------
9分
(3)单调递增区间:,
单调递减区间………………12分
20.
(本题12分)
解:(1)因为时,,由函数式 得 ,
所以.--------------------4分
(2)因为,所以该商品每日的销售量为,.
每日销售该商品所获得的利润为,.----7分
当时
21.(本题12分)
解:(1)∵方程有两等根,即有两等根,
∴,解得; ………………………………………2分
∵,得,……………………………4分
∴是函数图象的对称轴,而此函数图象的对称轴是直线,
∴,∴,故.
……………………………6分
(2)∵函数的图象的对称轴为,,
∴当时,在上是增函数,∴,………………………8分
当时,在上是增函数,在上是减函数,∴,…10分
综上,.……………………………12分
22.解:(Ⅰ)由得
∴ 函数的定义域为,关于原点对称 ……………1分
∵ ………………………………………2分
∴ ………………3分
∴ 函数为奇函数 ……………………………………………………4分
(Ⅱ)任取,且,则
………………………5分
∵
⑴ 当时,
∴
∴ ,即
∴ 在为增函数 ……………………………………………6分
⑵ 当时,
∴
∴ ,即
∴ 在为减函数 ……………………………………………8分
由(Ⅰ)知,函数为奇函数,其图象关于原点对称
∴ 当时,函数的递增区间为和;当时,函数的递减
区间为和. ……………………………………………9分
(Ⅲ)由(Ⅱ)可知,当时,函数在区间和均上为减函数,则
当时,
………………………………………………………………………………………10分
当时,
………………………………………………………………………………………11分
∴ 函数在上的
最大值为,最小值为.
……………………………………………………………………………………12分
得分
同课章节目录
