湖南省郴州市中学2015-2016学年九年级下期中数学试卷含答案解析
文档属性
| 名称 | 湖南省郴州市中学2015-2016学年九年级下期中数学试卷含答案解析 |
|
|
| 格式 | zip | ||
| 文件大小 | 244.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-06 00:00:00 | ||
图片预览



文档简介
2015-2016学年湖南省郴州市XX中学九年级(下)期中数学试卷
一、选择题(共8小题,每小题3分,满分24分)
1.的相反数是( )
A.
B.2016
C.﹣
D.﹣2016
2.计算(﹣3)2的结果是( )
A.﹣6
B.6
C.﹣9
D.9
3.下列计算正确的是( )
A.a2+a2=a4
B.(a2)3=a5
C.2a﹣a=2
D.(ab)2=a2b2
4.下列四个几何体中,它们的主视图、左视图、俯视图都是正方形的是( )
A.
B.
C.
D.
5.以下图形既是轴对称图形,又是中心对称图形的是( )
A.等腰三角形
B.平行四边形
C.矩形
D.等腰梯形
6.已知圆锥的母线长为3,底面的半径为2,则圆锥的侧面积是( )
A.4π
B.6π
C.10π
D.12π
7.某射击运动员在一次射击练习中,成绩(单位:环)记录如下:8,9,8,7,10.这组数据的平均数和中位数分别是( )
A.8,8
B.8.4,8
C.8.4,8.4
D.8,8.4
8.如图,在矩形ABCD中,AB=3,将△ABD沿对角线BD对折,得到△EBD,DE与BC交于点F,∠ADB=30°,则EF=( )
A.
B.2
C.3
D.3
二、填空题.(共8小题,每小题3分,满分24分)
9.根据相关部门统计,2014年我国共有9390000名学生参加高考,9390000用科学记数法表示为 .
10.若点P1(﹣1,m),P2(﹣2,n)在反比例函数y=(k>0)的图象上,则m n(填“>”“<”或“=”号).
11.分解因式:2x2﹣2= .
12.函数中自变量x的取值范围是 .
13.如图,在△ABC中,若E是AB的中点,F是AC的中点,∠B=50°,则∠AEF= .
14.如图,已知A、B、C三点都在⊙O上,∠AOB=60°,∠ACB= .
15.在m2□6m□9的“□”中任意填上“+”或“﹣”号,所得的代数式为完全平方式的概率为 .
16.如图,按此规律,第6行最后一个数字是 ,第 行最后一个数是2014.
三、解答题(17~19每题6分,20~23每题8分,24~25每题10分,26题12分,共82分)
17.计算:(1﹣)0+(﹣1)2016﹣tan30°+()﹣2.
18.解方程组.
19.在13×13的网格图中,已知△ABC和点M(1,2).
(1)以点M为位似中心,位似比为2,画出△ABC的位似图形△A′B′C′;
(2)写出△A′B′C′的各顶点坐标.
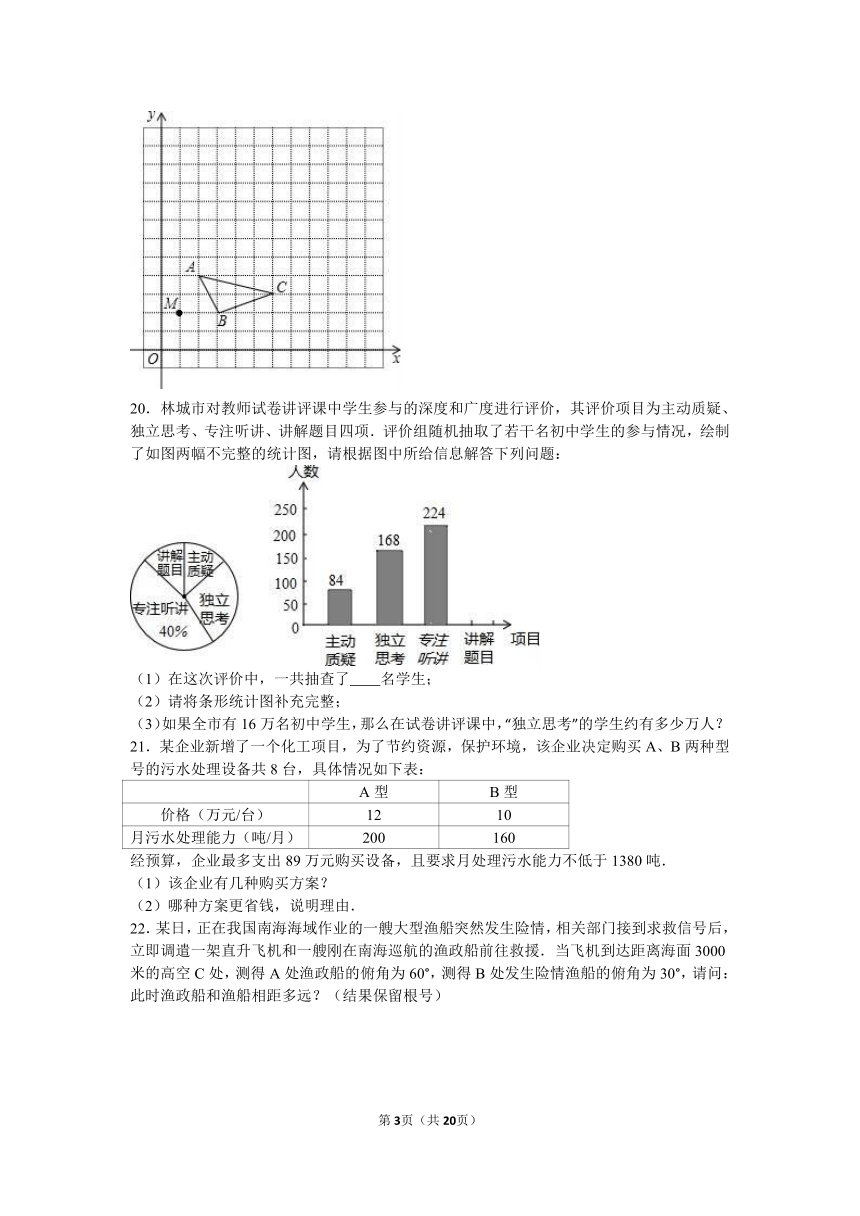
20.林城市对教师试卷讲评课中学生参与的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如图两幅不完整的统计图,请根据图中所给信息解答下列问题:
(1)在这次评价中,一共抽查了 名学生;
(2)请将条形统计图补充完整;
(3)如果全市有16万名初中学生,那么在试卷讲评课中,“独立思考”的学生约有多少万人?
21.某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共8台,具体情况如下表:
A型
B型
价格(万元/台)
12
10
月污水处理能力(吨/月)
200
160
经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低于1380吨.
(1)该企业有几种购买方案?
(2)哪种方案更省钱,说明理由.
22.某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)
23.如图,已知四边形ABCD是平行四边形,点E、B、D、F在同一直线上,且BE=DF.求证:AE=CF.
24.先阅读,后解答:
===3+
像上述解题过程中,﹣与+相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
(1)的有理化因式是 ;
+2的有理化因式是 .
(2)将下列式子进行分母有理化:
= ;
= .
(3)已知a=,b=2﹣,比较a与b的大小关系.
25.如图,已知抛物线经过点A(4,0),B(0,4),C(6,6).
(1)求抛物线的表达式;
(2)证明:四边形AOBC的两条对角线互相垂直;
(3)在四边形AOBC的内部能否截出面积最大的 DEFG?(顶点D,E,F,G分别在线段AO,OB,BC,CA上,且不与四边形AOBC的顶点重合)若能,求出 DEFG的最大面积,并求出此时点D的坐标;若不能,请说明理由.
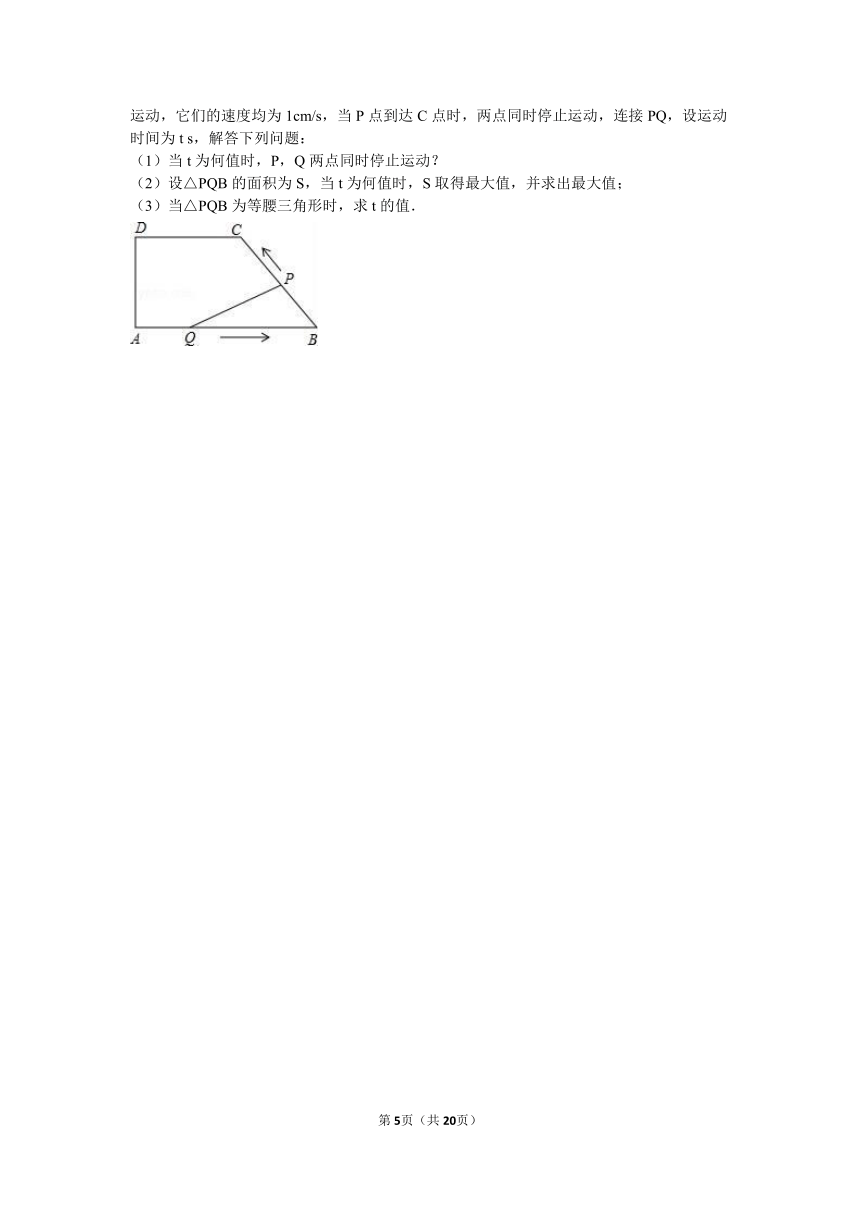
26.如图,在四边形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为1cm/s,当P点到达C点时,两点同时停止运动,连接PQ,设运动时间为t
s,解答下列问题:
(1)当t为何值时,P,Q两点同时停止运动?
(2)设△PQB的面积为S,当t为何值时,S取得最大值,并求出最大值;
(3)当△PQB为等腰三角形时,求t的值.
2015-2016学年湖南省郴州市XX中学九年级(下)期中数学试卷
参考答案与试题解析
一、选择题(共8小题,每小题3分,满分24分)
1.的相反数是( )
A.
B.2016
C.﹣
D.﹣2016
【考点】相反数.
【分析】根据相反数的意义,只有符号不同的数为相反数.
【解答】解:的相反数是﹣,
故选:C.
2.计算(﹣3)2的结果是( )
A.﹣6
B.6
C.﹣9
D.9
【考点】有理数的乘方.
【分析】根据有理数的乘方运算,乘方的运算可以利用乘法的运算来进行.
【解答】解:(﹣3)2=(﹣3)×(﹣3)=9.
故选:D.
3.下列计算正确的是( )
A.a2+a2=a4
B.(a2)3=a5
C.2a﹣a=2
D.(ab)2=a2b2
【考点】幂的乘方与积的乘方;合并同类项.
【分析】结合选项分别进行幂的乘方和积的乘方、合并同类项等运算,然后选择正确选项.
【解答】解:A、a2+a2=2a2,原式错误,故本选项错误;
B、(a2)3=a6,原式错误,故本选项错误;
C、2a﹣a=a,原式错误,故本选项错误;
D、(ab)2=a2b2,原式正确,故本选项正确.
故选D.
4.下列四个几何体中,它们的主视图、左视图、俯视图都是正方形的是( )
A.
B.
C.
D.
【考点】简单几何体的三视图.
【分析】分别分析四个选项的主视图、左视图、俯视图,从而得出都是正方体的几何体.
【解答】解:A、正方体的主视图、左视图、俯视图都正方形,符合题意;
B、圆柱的主视图、左视图都是矩形、俯视图是圆,不符合题意;
C、圆锥主视图、左视图都是等腰三角形,俯视图是圆和圆中间一点,不符合题意;
D、球的主视图、左视图、俯视图都是圆,不符合题意.
故选A.
5.以下图形既是轴对称图形,又是中心对称图形的是( )
A.等腰三角形
B.平行四边形
C.矩形
D.等腰梯形
【考点】中心对称图形;轴对称图形.
【分析】根据轴对称图形与中心对称图形的概念求解.
【解答】解:A、是轴对称图形,不是中心对称图形;
B、是中心对称图形,不是轴对称图形;
C、是中心对称图形,也是轴对称图形;
D、不是中心对称图形,是轴对称图形.
故选:C.
6.已知圆锥的母线长为3,底面的半径为2,则圆锥的侧面积是( )
A.4π
B.6π
C.10π
D.12π
【考点】圆锥的计算.
【分析】根据锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式计算即可.
【解答】解:圆锥的侧面积= 2π 2 3=6π.
故选:B.
7.某射击运动员在一次射击练习中,成绩(单位:环)记录如下:8,9,8,7,10.这组数据的平均数和中位数分别是( )
A.8,8
B.8.4,8
C.8.4,8.4
D.8,8.4
【考点】中位数;算术平均数.
【分析】根据平均数公式求解即可,即用所有数据的和除以5即可;5个数据的中位数是排序后的第三个数.
【解答】解:8,9,8,7,10的平均数为×(8+9+8+7+10)=8.4.
8,9,8,7,10排序后为7,8,8,9,10,
故中位数为8.
故选B.
8.如图,在矩形ABCD中,AB=3,将△ABD沿对角线BD对折,得到△EBD,DE与BC交于点F,∠ADB=30°,则EF=( )
A.
B.2
C.3
D.3
【考点】翻折变换(折叠问题).
【分析】利用翻折变换的性质得出:∠1=∠2=30°,进而结合锐角三角函数关系求出FE的长.
【解答】解:如图所示:由题意可得:∠1=∠2=30°,则∠3=30°,
可得∠4=∠5=60°,
∵AB=DC=BE=3,
∴tan60°===,
解得:EF=.
故选:A.
二、填空题.(共8小题,每小题3分,满分24分)
9.根据相关部门统计,2014年我国共有9390000名学生参加高考,9390000用科学记数法表示为 9.39×106 .
【考点】科学记数法—表示较大的数.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:9390000用科学记数法表示为9.39×106,
故答案为:9.39×106.
10.若点P1(﹣1,m),P2(﹣2,n)在反比例函数y=(k>0)的图象上,则m < n(填“>”“<”或“=”号).
【考点】反比例函数图象上点的坐标特征.
【分析】根据反比例函数图象上点的坐标特征得到﹣1 m=k,﹣2 n=k,解得m=﹣k,n=﹣,然后利用k>0比较m、n的大小.
【解答】解:∵P1(﹣1,m),P2(﹣2,n)在反比例函数y=(k>0)的图象上,
∴﹣1 m=k,﹣2 n=k,
∴m=﹣k,n=﹣,
而k>0,
∴m<n.
故答案为:<.
11.分解因式:2x2﹣2= 2(x+1)(x﹣1) .
【考点】提公因式法与公式法的综合运用.
【分析】先提取公因式2,再根据平方差公式进行二次分解即可求得答案.
【解答】解:2x2﹣2=2(x2﹣1)=2(x+1)(x﹣1).
故答案为:2(x+1)(x﹣1).
12.函数中自变量x的取值范围是 x≥2 .
【考点】函数自变量的取值范围.
【分析】根据二次根式的性质,被开方数大于等于0,就可以求解.
【解答】解:依题意,得x﹣2≥0,
解得:x≥2,
故答案为:x≥2.
13.如图,在△ABC中,若E是AB的中点,F是AC的中点,∠B=50°,则∠AEF= 50° .
【考点】三角形中位线定理.
【分析】根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC,再根据两直线平行,同位角相等可得∠AEF=∠B.
【解答】解:∵E是AB的中点,F是AC的中点,
∴EF是△ABC的中位线,
∴EF∥BC,
∴∠AEF=∠B=50°.
故答案为:50°.
14.如图,已知A、B、C三点都在⊙O上,∠AOB=60°,∠ACB= 30° .
【考点】圆周角定理.
【分析】由∠ACB是⊙O的圆周角,∠AOB是圆心角,且∠AOB=60°,根据圆周角定理,即可求得圆周角∠ACB的度数.
【解答】解:如图,∵∠AOB=60°,
∴∠ACB=∠AOB=30°.
故答案是:30°.
15.在m2□6m□9的“□”中任意填上“+”或“﹣”号,所得的代数式为完全平方式的概率为 .
【考点】列表法与树状图法;完全平方式.
【分析】先画树状图展示所有四种等可能的结果数,再根据完全平方式的定义得到“++”和“﹣+”能使所得的代数式为完全平方式,然后根据概率公式求解.
【解答】解:画树状图为:
共有四种等可能的结果数,其中“++”和“﹣+”能使所得的代数式为完全平方式,
所以所得的代数式为完全平方式的概率==.
故答案为.
16.如图,按此规律,第6行最后一个数字是 16 ,第 672 行最后一个数是2014.
【考点】规律型:数字的变化类.
【分析】每一行的最后一个数字分别是1,4,7,10…,易得第n行的最后一个数字为1+3(n﹣1)=3n﹣2,由此求得第6行最后一个数字,建立方程求得最后一个数是2014在哪一行.
【解答】解:每一行的最后一个数分别是1,4,7,10…,
第n行的最后一个数字为1+3(n﹣1)=3n﹣2,
∴第6行最后一个数字是3×6﹣2=16;
3n﹣2=2014
解得n=672.
因此第6行最后一个数字是16,第672行最后一个数是2014.
故答案为:16,672.
三、解答题(17~19每题6分,20~23每题8分,24~25每题10分,26题12分,共82分)
17.计算:(1﹣)0+(﹣1)2016﹣tan30°+()﹣2.
【考点】实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.
【分析】原式利用零指数幂、负整数指数幂法则,乘方的意义,以及特殊角的三角函数值计算即可得到结果.
【解答】解:原式=1+1﹣1+9=10.
18.解方程组.
【考点】解二元一次方程组.
【分析】根据y的系数互为相反数,利用加减消元法求解即可.
【解答】解:,
①+②得,4x=20,
解得x=5,
把x=5代入①得,5﹣y=8,
解得y=﹣3,
所以方程组的解是.
19.在13×13的网格图中,已知△ABC和点M(1,2).
(1)以点M为位似中心,位似比为2,画出△ABC的位似图形△A′B′C′;
(2)写出△A′B′C′的各顶点坐标.
【考点】作图-位似变换.
【分析】(1)利用位似图形的性质即可位似比为2,进而得出各对应点位置;
(2)利用所画图形得出对应点坐标即可.
【解答】解:(1)如图所示:△A′B′C′即为所求;
(2)△A′B′C′的各顶点坐标分别为:A′(3,6),B′(5,2),C′(11,4).
20.林城市对教师试卷讲评课中学生参与的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如图两幅不完整的统计图,请根据图中所给信息解答下列问题:
(1)在这次评价中,一共抽查了 560 名学生;
(2)请将条形统计图补充完整;
(3)如果全市有16万名初中学生,那么在试卷讲评课中,“独立思考”的学生约有多少万人?
【考点】条形统计图;用样本估计总体;扇形统计图.
【分析】(1)根据扇形统计图专注听讲的百分比与条形统计图中专注听讲的人数,列式计算即可;
(2)用被抽查的学生人数减去主动质疑、独立思考、专注听讲的人数,求出讲解题目的人数,然后补全统计图即可;
(3)用独立思考的学生的百分比乘以16万,进行计算即可得解.
【解答】解:(1)224÷40%=560名;
(2)讲解题目的学生数为:560﹣84﹣168﹣224=560﹣476=84,
补全统计图如图;
(3)×16=4.8万,
答:在试卷讲评课中,“独立思考”的学生约有4.8万人.
21.某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共8台,具体情况如下表:
A型
B型
价格(万元/台)
12
10
月污水处理能力(吨/月)
200
160
经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低于1380吨.
(1)该企业有几种购买方案?
(2)哪种方案更省钱,说明理由.
【考点】一元一次不等式组的应用.
【分析】(1)设购买污水处理设备A型号x台,则购买B型号(8﹣x)台,根据企业最多支出89万元购买设备,要求月处理污水能力不低于1380吨,列出不等式组,然后找出最合适的方案即可.
(2)计算出每一方案的花费,通过比较即可得到答案.
【解答】解:设购买污水处理设备A型号x台,则购买B型号(8﹣x)台,
根据题意,得
,
解这个不等式组,得:2.5≤x≤4.5.
∵x是整数,
∴x=3或x=4.
当x=3时,8﹣x=5;
当x=4时,8﹣x=4.
答:有2种购买方案:第一种是购买3台A型污水处理设备,5台B型污水处理设备;
第二种是购买4台A型污水处理设备,4台B型污水处理设备;
(2)当x=3时,购买资金为12×3+10×5=86(万元),
当x=4时,购买资金为12×4+10×4=88(万元).
因为88>86,
所以为了节约资金,应购污水处理设备A型号3台,B型号5台.
答:购买3台A型污水处理设备,5台B型污水处理设备更省钱.
22.某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)
【考点】解直角三角形的应用-仰角俯角问题.
【分析】在Rt△CDB中求出BD,在Rt△CDA中求出AD,继而可得AB,也即此时渔政船和渔船的距离.
【解答】解:在Rt△CDA中,∠ACD=30°,CD=3000米,
∴AD=CDtan∠ACD=1000米,
在Rt△CDB中,∠BCD=60°,
∴BD=CDtan∠BCD=3000米,
∴AB=BD﹣AD=2000米.
答:此时渔政船和渔船相距2000米.
23.如图,已知四边形ABCD是平行四边形,点E、B、D、F在同一直线上,且BE=DF.求证:AE=CF.
【考点】全等三角形的判定与性质;平行四边形的性质.
【分析】根据平行四边形的对边相等可得AB=CD,AB∥CD,再根据两直线平行,内错角相等可得∠ABD=∠CDB,然后求出∠ABE=∠CDF,再利用“边角边”证明△ABE和△CDF全等,根据全等三角形对应边相等证明即可.
【解答】证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABD=∠CDB,
∴180°﹣∠ABD=180°﹣∠CDB,
即∠ABE=∠CDF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴AE=CF.
24.先阅读,后解答:
===3+
像上述解题过程中,﹣与+相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
(1)的有理化因式是 ;
+2的有理化因式是 ﹣2 .
(2)将下列式子进行分母有理化:
= ;
= 1﹣ .
(3)已知a=,b=2﹣,比较a与b的大小关系.
【考点】分母有理化;实数大小比较.
【分析】(1)根据题意找出各式的有理化因式即可;
(2)各式分母有理化即可;
(3)把a分母有理化,比较即可.
【解答】解:(1)的有理化因式是,
+2的有理化因式是﹣2;
故答案为:;﹣2;
(2)原式=;原式==1﹣;
故答案为:;1﹣;
(3)a==2﹣=b.
25.如图,已知抛物线经过点A(4,0),B(0,4),C(6,6).
(1)求抛物线的表达式;
(2)证明:四边形AOBC的两条对角线互相垂直;
(3)在四边形AOBC的内部能否截出面积最大的 DEFG?(顶点D,E,F,G分别在线段AO,OB,BC,CA上,且不与四边形AOBC的顶点重合)若能,求出 DEFG的最大面积,并求出此时点D的坐标;若不能,请说明理由.
【考点】二次函数综合题.
【分析】(1)根据抛物线经过点A(4,0),B(0,4),C(6,6),利用待定系数法,求出抛物线的表达式即可;
(2)利用两点间的距离公式分别计算出OA=4,OB=4,CB=2,CA=2,则OA=OB,CA=CB,根据线段垂直平分线定理的逆定理得到OC垂直平分AB,所以四边形AOBC的两条对角线互相垂直;
(3)如图2,利用两点间的距离公式分别计算出AB=4,OC=6,设D(t,0),根据平行四边形的性质四边形DEFG为平行四边形得到EF∥DG,EF=DG,再由OC垂直平分AB得到△OBC与△OAC关于OC对称,则可判断EF和DG为对应线段,所以四边形DEFG为矩形,DG∥OC,则DE∥AB,于是可判断△ODE∽△OAB,利用相似比得DE=t,接着证明△ADG∽△AOC,利用相似比得DG=(4﹣t),所以矩形DEFG的面积=DE DG=t (4﹣t)=﹣3t2+12t,然后根据二次函数的性质求平行四边形DEFG的面积的最大值,从而得到此时D点坐标.
【解答】解:(1)设该抛物线的解析式为y=ax2+bx+c,
根据题意得,解得,
∴抛物线的表达式为y=x2﹣x+4;
(2)如图1,连结AB、OC,
∵A(4,0),B(0,4),C(6,6),
∴OA=4,OB=4,CB==2,CA==2,
∴OA=OB,CA=CB,
∴OC垂直平分AB,
即四边形AOBC的两条对角线互相垂直;
(3)能.
如图2,AB==4,OC==6,设D(t,0),
∵四边形DEFG为平行四边形,
∴EF∥DG,EF=DG,
∵OC垂直平分AB,
∴△OBC与△OAC关于OC对称,
∴EF和DG为对应线段,
∴四边形DEFG为矩形,DG∥OC,
∴DE∥AB,
∴△ODE∽△OAB,
∴=,即=,解得DE=t,
∵DG∥OC,
∴△ADG∽△AOC,
∴=,即=,解得DG=(4﹣t),
∴矩形DEFG的面积=DE DG=t (4﹣t)=﹣3t2+12t=﹣3(t﹣2)2+12,
当t=2时,平行四边形DEFG的面积最大,最大值为12,此时D点坐标为(2,0).
26.如图,在四边形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为1cm/s,当P点到达C点时,两点同时停止运动,连接PQ,设运动时间为t
s,解答下列问题:
(1)当t为何值时,P,Q两点同时停止运动?
(2)设△PQB的面积为S,当t为何值时,S取得最大值,并求出最大值;
(3)当△PQB为等腰三角形时,求t的值.
【考点】四边形综合题.
【分析】(1)通过比较线段AB,BC的大小,找出较短的线段,根据速度公式可以直接求得;
(2)由已知条件,把△PQB的边QB用含t的代数式表示出来,三角形的高可由相似三角形的性质也用含t的代数式表示出来,代入三角形的面积公式可得到一个二次函数,即可求出S的最值;
(3)根据等腰三角形的性质和余弦公式列出等式求解,即可求的结论.
【解答】解:(1)作CE⊥AB于E,
∵DC∥AB,DA⊥AB,
∴四边形AECD是矩形,
∴AE=CD=5,CE=AD=4,
∴BE=3,
∴BC=,
∴BC<AB,
∴P到C时,P、Q同时停止运动,
∴t=(秒),
即t=5秒时,P,Q两点同时停止运动.
(2)由题意知,AQ=BP=t,
∴QB=8﹣t,
作PF⊥QB于F,则△BPF~△BCE,
∴,即,
∴BF=,
∴S=QB PF=×(8﹣t)==﹣(t﹣4)2+(0<t≤5),
∵﹣<0,
∴S有最大值,当t=4时,S的最大值是;
(3)∵cos∠B=,
①当PQ=PB时(如图2所示),则BG=BQ,
==,解得t=s,
②当PQ=BQ时(如图3所示),则BG=PB,
==,解得t=s,
③当BP=BQ时(如图4所示),则8﹣t=t,
解得:t=4.
综上所述:当t=s,
s或t=4s时,△PQB为等腰三角形.
2016年11月23日
第6页(共20页)
一、选择题(共8小题,每小题3分,满分24分)
1.的相反数是( )
A.
B.2016
C.﹣
D.﹣2016
2.计算(﹣3)2的结果是( )
A.﹣6
B.6
C.﹣9
D.9
3.下列计算正确的是( )
A.a2+a2=a4
B.(a2)3=a5
C.2a﹣a=2
D.(ab)2=a2b2
4.下列四个几何体中,它们的主视图、左视图、俯视图都是正方形的是( )
A.
B.
C.
D.
5.以下图形既是轴对称图形,又是中心对称图形的是( )
A.等腰三角形
B.平行四边形
C.矩形
D.等腰梯形
6.已知圆锥的母线长为3,底面的半径为2,则圆锥的侧面积是( )
A.4π
B.6π
C.10π
D.12π
7.某射击运动员在一次射击练习中,成绩(单位:环)记录如下:8,9,8,7,10.这组数据的平均数和中位数分别是( )
A.8,8
B.8.4,8
C.8.4,8.4
D.8,8.4
8.如图,在矩形ABCD中,AB=3,将△ABD沿对角线BD对折,得到△EBD,DE与BC交于点F,∠ADB=30°,则EF=( )
A.
B.2
C.3
D.3
二、填空题.(共8小题,每小题3分,满分24分)
9.根据相关部门统计,2014年我国共有9390000名学生参加高考,9390000用科学记数法表示为 .
10.若点P1(﹣1,m),P2(﹣2,n)在反比例函数y=(k>0)的图象上,则m n(填“>”“<”或“=”号).
11.分解因式:2x2﹣2= .
12.函数中自变量x的取值范围是 .
13.如图,在△ABC中,若E是AB的中点,F是AC的中点,∠B=50°,则∠AEF= .
14.如图,已知A、B、C三点都在⊙O上,∠AOB=60°,∠ACB= .
15.在m2□6m□9的“□”中任意填上“+”或“﹣”号,所得的代数式为完全平方式的概率为 .
16.如图,按此规律,第6行最后一个数字是 ,第 行最后一个数是2014.
三、解答题(17~19每题6分,20~23每题8分,24~25每题10分,26题12分,共82分)
17.计算:(1﹣)0+(﹣1)2016﹣tan30°+()﹣2.
18.解方程组.
19.在13×13的网格图中,已知△ABC和点M(1,2).
(1)以点M为位似中心,位似比为2,画出△ABC的位似图形△A′B′C′;
(2)写出△A′B′C′的各顶点坐标.
20.林城市对教师试卷讲评课中学生参与的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如图两幅不完整的统计图,请根据图中所给信息解答下列问题:
(1)在这次评价中,一共抽查了 名学生;
(2)请将条形统计图补充完整;
(3)如果全市有16万名初中学生,那么在试卷讲评课中,“独立思考”的学生约有多少万人?
21.某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共8台,具体情况如下表:
A型
B型
价格(万元/台)
12
10
月污水处理能力(吨/月)
200
160
经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低于1380吨.
(1)该企业有几种购买方案?
(2)哪种方案更省钱,说明理由.
22.某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)
23.如图,已知四边形ABCD是平行四边形,点E、B、D、F在同一直线上,且BE=DF.求证:AE=CF.
24.先阅读,后解答:
===3+
像上述解题过程中,﹣与+相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
(1)的有理化因式是 ;
+2的有理化因式是 .
(2)将下列式子进行分母有理化:
= ;
= .
(3)已知a=,b=2﹣,比较a与b的大小关系.
25.如图,已知抛物线经过点A(4,0),B(0,4),C(6,6).
(1)求抛物线的表达式;
(2)证明:四边形AOBC的两条对角线互相垂直;
(3)在四边形AOBC的内部能否截出面积最大的 DEFG?(顶点D,E,F,G分别在线段AO,OB,BC,CA上,且不与四边形AOBC的顶点重合)若能,求出 DEFG的最大面积,并求出此时点D的坐标;若不能,请说明理由.
26.如图,在四边形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为1cm/s,当P点到达C点时,两点同时停止运动,连接PQ,设运动时间为t
s,解答下列问题:
(1)当t为何值时,P,Q两点同时停止运动?
(2)设△PQB的面积为S,当t为何值时,S取得最大值,并求出最大值;
(3)当△PQB为等腰三角形时,求t的值.
2015-2016学年湖南省郴州市XX中学九年级(下)期中数学试卷
参考答案与试题解析
一、选择题(共8小题,每小题3分,满分24分)
1.的相反数是( )
A.
B.2016
C.﹣
D.﹣2016
【考点】相反数.
【分析】根据相反数的意义,只有符号不同的数为相反数.
【解答】解:的相反数是﹣,
故选:C.
2.计算(﹣3)2的结果是( )
A.﹣6
B.6
C.﹣9
D.9
【考点】有理数的乘方.
【分析】根据有理数的乘方运算,乘方的运算可以利用乘法的运算来进行.
【解答】解:(﹣3)2=(﹣3)×(﹣3)=9.
故选:D.
3.下列计算正确的是( )
A.a2+a2=a4
B.(a2)3=a5
C.2a﹣a=2
D.(ab)2=a2b2
【考点】幂的乘方与积的乘方;合并同类项.
【分析】结合选项分别进行幂的乘方和积的乘方、合并同类项等运算,然后选择正确选项.
【解答】解:A、a2+a2=2a2,原式错误,故本选项错误;
B、(a2)3=a6,原式错误,故本选项错误;
C、2a﹣a=a,原式错误,故本选项错误;
D、(ab)2=a2b2,原式正确,故本选项正确.
故选D.
4.下列四个几何体中,它们的主视图、左视图、俯视图都是正方形的是( )
A.
B.
C.
D.
【考点】简单几何体的三视图.
【分析】分别分析四个选项的主视图、左视图、俯视图,从而得出都是正方体的几何体.
【解答】解:A、正方体的主视图、左视图、俯视图都正方形,符合题意;
B、圆柱的主视图、左视图都是矩形、俯视图是圆,不符合题意;
C、圆锥主视图、左视图都是等腰三角形,俯视图是圆和圆中间一点,不符合题意;
D、球的主视图、左视图、俯视图都是圆,不符合题意.
故选A.
5.以下图形既是轴对称图形,又是中心对称图形的是( )
A.等腰三角形
B.平行四边形
C.矩形
D.等腰梯形
【考点】中心对称图形;轴对称图形.
【分析】根据轴对称图形与中心对称图形的概念求解.
【解答】解:A、是轴对称图形,不是中心对称图形;
B、是中心对称图形,不是轴对称图形;
C、是中心对称图形,也是轴对称图形;
D、不是中心对称图形,是轴对称图形.
故选:C.
6.已知圆锥的母线长为3,底面的半径为2,则圆锥的侧面积是( )
A.4π
B.6π
C.10π
D.12π
【考点】圆锥的计算.
【分析】根据锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式计算即可.
【解答】解:圆锥的侧面积= 2π 2 3=6π.
故选:B.
7.某射击运动员在一次射击练习中,成绩(单位:环)记录如下:8,9,8,7,10.这组数据的平均数和中位数分别是( )
A.8,8
B.8.4,8
C.8.4,8.4
D.8,8.4
【考点】中位数;算术平均数.
【分析】根据平均数公式求解即可,即用所有数据的和除以5即可;5个数据的中位数是排序后的第三个数.
【解答】解:8,9,8,7,10的平均数为×(8+9+8+7+10)=8.4.
8,9,8,7,10排序后为7,8,8,9,10,
故中位数为8.
故选B.
8.如图,在矩形ABCD中,AB=3,将△ABD沿对角线BD对折,得到△EBD,DE与BC交于点F,∠ADB=30°,则EF=( )
A.
B.2
C.3
D.3
【考点】翻折变换(折叠问题).
【分析】利用翻折变换的性质得出:∠1=∠2=30°,进而结合锐角三角函数关系求出FE的长.
【解答】解:如图所示:由题意可得:∠1=∠2=30°,则∠3=30°,
可得∠4=∠5=60°,
∵AB=DC=BE=3,
∴tan60°===,
解得:EF=.
故选:A.
二、填空题.(共8小题,每小题3分,满分24分)
9.根据相关部门统计,2014年我国共有9390000名学生参加高考,9390000用科学记数法表示为 9.39×106 .
【考点】科学记数法—表示较大的数.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:9390000用科学记数法表示为9.39×106,
故答案为:9.39×106.
10.若点P1(﹣1,m),P2(﹣2,n)在反比例函数y=(k>0)的图象上,则m < n(填“>”“<”或“=”号).
【考点】反比例函数图象上点的坐标特征.
【分析】根据反比例函数图象上点的坐标特征得到﹣1 m=k,﹣2 n=k,解得m=﹣k,n=﹣,然后利用k>0比较m、n的大小.
【解答】解:∵P1(﹣1,m),P2(﹣2,n)在反比例函数y=(k>0)的图象上,
∴﹣1 m=k,﹣2 n=k,
∴m=﹣k,n=﹣,
而k>0,
∴m<n.
故答案为:<.
11.分解因式:2x2﹣2= 2(x+1)(x﹣1) .
【考点】提公因式法与公式法的综合运用.
【分析】先提取公因式2,再根据平方差公式进行二次分解即可求得答案.
【解答】解:2x2﹣2=2(x2﹣1)=2(x+1)(x﹣1).
故答案为:2(x+1)(x﹣1).
12.函数中自变量x的取值范围是 x≥2 .
【考点】函数自变量的取值范围.
【分析】根据二次根式的性质,被开方数大于等于0,就可以求解.
【解答】解:依题意,得x﹣2≥0,
解得:x≥2,
故答案为:x≥2.
13.如图,在△ABC中,若E是AB的中点,F是AC的中点,∠B=50°,则∠AEF= 50° .
【考点】三角形中位线定理.
【分析】根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC,再根据两直线平行,同位角相等可得∠AEF=∠B.
【解答】解:∵E是AB的中点,F是AC的中点,
∴EF是△ABC的中位线,
∴EF∥BC,
∴∠AEF=∠B=50°.
故答案为:50°.
14.如图,已知A、B、C三点都在⊙O上,∠AOB=60°,∠ACB= 30° .
【考点】圆周角定理.
【分析】由∠ACB是⊙O的圆周角,∠AOB是圆心角,且∠AOB=60°,根据圆周角定理,即可求得圆周角∠ACB的度数.
【解答】解:如图,∵∠AOB=60°,
∴∠ACB=∠AOB=30°.
故答案是:30°.
15.在m2□6m□9的“□”中任意填上“+”或“﹣”号,所得的代数式为完全平方式的概率为 .
【考点】列表法与树状图法;完全平方式.
【分析】先画树状图展示所有四种等可能的结果数,再根据完全平方式的定义得到“++”和“﹣+”能使所得的代数式为完全平方式,然后根据概率公式求解.
【解答】解:画树状图为:
共有四种等可能的结果数,其中“++”和“﹣+”能使所得的代数式为完全平方式,
所以所得的代数式为完全平方式的概率==.
故答案为.
16.如图,按此规律,第6行最后一个数字是 16 ,第 672 行最后一个数是2014.
【考点】规律型:数字的变化类.
【分析】每一行的最后一个数字分别是1,4,7,10…,易得第n行的最后一个数字为1+3(n﹣1)=3n﹣2,由此求得第6行最后一个数字,建立方程求得最后一个数是2014在哪一行.
【解答】解:每一行的最后一个数分别是1,4,7,10…,
第n行的最后一个数字为1+3(n﹣1)=3n﹣2,
∴第6行最后一个数字是3×6﹣2=16;
3n﹣2=2014
解得n=672.
因此第6行最后一个数字是16,第672行最后一个数是2014.
故答案为:16,672.
三、解答题(17~19每题6分,20~23每题8分,24~25每题10分,26题12分,共82分)
17.计算:(1﹣)0+(﹣1)2016﹣tan30°+()﹣2.
【考点】实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.
【分析】原式利用零指数幂、负整数指数幂法则,乘方的意义,以及特殊角的三角函数值计算即可得到结果.
【解答】解:原式=1+1﹣1+9=10.
18.解方程组.
【考点】解二元一次方程组.
【分析】根据y的系数互为相反数,利用加减消元法求解即可.
【解答】解:,
①+②得,4x=20,
解得x=5,
把x=5代入①得,5﹣y=8,
解得y=﹣3,
所以方程组的解是.
19.在13×13的网格图中,已知△ABC和点M(1,2).
(1)以点M为位似中心,位似比为2,画出△ABC的位似图形△A′B′C′;
(2)写出△A′B′C′的各顶点坐标.
【考点】作图-位似变换.
【分析】(1)利用位似图形的性质即可位似比为2,进而得出各对应点位置;
(2)利用所画图形得出对应点坐标即可.
【解答】解:(1)如图所示:△A′B′C′即为所求;
(2)△A′B′C′的各顶点坐标分别为:A′(3,6),B′(5,2),C′(11,4).
20.林城市对教师试卷讲评课中学生参与的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如图两幅不完整的统计图,请根据图中所给信息解答下列问题:
(1)在这次评价中,一共抽查了 560 名学生;
(2)请将条形统计图补充完整;
(3)如果全市有16万名初中学生,那么在试卷讲评课中,“独立思考”的学生约有多少万人?
【考点】条形统计图;用样本估计总体;扇形统计图.
【分析】(1)根据扇形统计图专注听讲的百分比与条形统计图中专注听讲的人数,列式计算即可;
(2)用被抽查的学生人数减去主动质疑、独立思考、专注听讲的人数,求出讲解题目的人数,然后补全统计图即可;
(3)用独立思考的学生的百分比乘以16万,进行计算即可得解.
【解答】解:(1)224÷40%=560名;
(2)讲解题目的学生数为:560﹣84﹣168﹣224=560﹣476=84,
补全统计图如图;
(3)×16=4.8万,
答:在试卷讲评课中,“独立思考”的学生约有4.8万人.
21.某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共8台,具体情况如下表:
A型
B型
价格(万元/台)
12
10
月污水处理能力(吨/月)
200
160
经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低于1380吨.
(1)该企业有几种购买方案?
(2)哪种方案更省钱,说明理由.
【考点】一元一次不等式组的应用.
【分析】(1)设购买污水处理设备A型号x台,则购买B型号(8﹣x)台,根据企业最多支出89万元购买设备,要求月处理污水能力不低于1380吨,列出不等式组,然后找出最合适的方案即可.
(2)计算出每一方案的花费,通过比较即可得到答案.
【解答】解:设购买污水处理设备A型号x台,则购买B型号(8﹣x)台,
根据题意,得
,
解这个不等式组,得:2.5≤x≤4.5.
∵x是整数,
∴x=3或x=4.
当x=3时,8﹣x=5;
当x=4时,8﹣x=4.
答:有2种购买方案:第一种是购买3台A型污水处理设备,5台B型污水处理设备;
第二种是购买4台A型污水处理设备,4台B型污水处理设备;
(2)当x=3时,购买资金为12×3+10×5=86(万元),
当x=4时,购买资金为12×4+10×4=88(万元).
因为88>86,
所以为了节约资金,应购污水处理设备A型号3台,B型号5台.
答:购买3台A型污水处理设备,5台B型污水处理设备更省钱.
22.某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)
【考点】解直角三角形的应用-仰角俯角问题.
【分析】在Rt△CDB中求出BD,在Rt△CDA中求出AD,继而可得AB,也即此时渔政船和渔船的距离.
【解答】解:在Rt△CDA中,∠ACD=30°,CD=3000米,
∴AD=CDtan∠ACD=1000米,
在Rt△CDB中,∠BCD=60°,
∴BD=CDtan∠BCD=3000米,
∴AB=BD﹣AD=2000米.
答:此时渔政船和渔船相距2000米.
23.如图,已知四边形ABCD是平行四边形,点E、B、D、F在同一直线上,且BE=DF.求证:AE=CF.
【考点】全等三角形的判定与性质;平行四边形的性质.
【分析】根据平行四边形的对边相等可得AB=CD,AB∥CD,再根据两直线平行,内错角相等可得∠ABD=∠CDB,然后求出∠ABE=∠CDF,再利用“边角边”证明△ABE和△CDF全等,根据全等三角形对应边相等证明即可.
【解答】证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABD=∠CDB,
∴180°﹣∠ABD=180°﹣∠CDB,
即∠ABE=∠CDF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴AE=CF.
24.先阅读,后解答:
===3+
像上述解题过程中,﹣与+相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
(1)的有理化因式是 ;
+2的有理化因式是 ﹣2 .
(2)将下列式子进行分母有理化:
= ;
= 1﹣ .
(3)已知a=,b=2﹣,比较a与b的大小关系.
【考点】分母有理化;实数大小比较.
【分析】(1)根据题意找出各式的有理化因式即可;
(2)各式分母有理化即可;
(3)把a分母有理化,比较即可.
【解答】解:(1)的有理化因式是,
+2的有理化因式是﹣2;
故答案为:;﹣2;
(2)原式=;原式==1﹣;
故答案为:;1﹣;
(3)a==2﹣=b.
25.如图,已知抛物线经过点A(4,0),B(0,4),C(6,6).
(1)求抛物线的表达式;
(2)证明:四边形AOBC的两条对角线互相垂直;
(3)在四边形AOBC的内部能否截出面积最大的 DEFG?(顶点D,E,F,G分别在线段AO,OB,BC,CA上,且不与四边形AOBC的顶点重合)若能,求出 DEFG的最大面积,并求出此时点D的坐标;若不能,请说明理由.
【考点】二次函数综合题.
【分析】(1)根据抛物线经过点A(4,0),B(0,4),C(6,6),利用待定系数法,求出抛物线的表达式即可;
(2)利用两点间的距离公式分别计算出OA=4,OB=4,CB=2,CA=2,则OA=OB,CA=CB,根据线段垂直平分线定理的逆定理得到OC垂直平分AB,所以四边形AOBC的两条对角线互相垂直;
(3)如图2,利用两点间的距离公式分别计算出AB=4,OC=6,设D(t,0),根据平行四边形的性质四边形DEFG为平行四边形得到EF∥DG,EF=DG,再由OC垂直平分AB得到△OBC与△OAC关于OC对称,则可判断EF和DG为对应线段,所以四边形DEFG为矩形,DG∥OC,则DE∥AB,于是可判断△ODE∽△OAB,利用相似比得DE=t,接着证明△ADG∽△AOC,利用相似比得DG=(4﹣t),所以矩形DEFG的面积=DE DG=t (4﹣t)=﹣3t2+12t,然后根据二次函数的性质求平行四边形DEFG的面积的最大值,从而得到此时D点坐标.
【解答】解:(1)设该抛物线的解析式为y=ax2+bx+c,
根据题意得,解得,
∴抛物线的表达式为y=x2﹣x+4;
(2)如图1,连结AB、OC,
∵A(4,0),B(0,4),C(6,6),
∴OA=4,OB=4,CB==2,CA==2,
∴OA=OB,CA=CB,
∴OC垂直平分AB,
即四边形AOBC的两条对角线互相垂直;
(3)能.
如图2,AB==4,OC==6,设D(t,0),
∵四边形DEFG为平行四边形,
∴EF∥DG,EF=DG,
∵OC垂直平分AB,
∴△OBC与△OAC关于OC对称,
∴EF和DG为对应线段,
∴四边形DEFG为矩形,DG∥OC,
∴DE∥AB,
∴△ODE∽△OAB,
∴=,即=,解得DE=t,
∵DG∥OC,
∴△ADG∽△AOC,
∴=,即=,解得DG=(4﹣t),
∴矩形DEFG的面积=DE DG=t (4﹣t)=﹣3t2+12t=﹣3(t﹣2)2+12,
当t=2时,平行四边形DEFG的面积最大,最大值为12,此时D点坐标为(2,0).
26.如图,在四边形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为1cm/s,当P点到达C点时,两点同时停止运动,连接PQ,设运动时间为t
s,解答下列问题:
(1)当t为何值时,P,Q两点同时停止运动?
(2)设△PQB的面积为S,当t为何值时,S取得最大值,并求出最大值;
(3)当△PQB为等腰三角形时,求t的值.
【考点】四边形综合题.
【分析】(1)通过比较线段AB,BC的大小,找出较短的线段,根据速度公式可以直接求得;
(2)由已知条件,把△PQB的边QB用含t的代数式表示出来,三角形的高可由相似三角形的性质也用含t的代数式表示出来,代入三角形的面积公式可得到一个二次函数,即可求出S的最值;
(3)根据等腰三角形的性质和余弦公式列出等式求解,即可求的结论.
【解答】解:(1)作CE⊥AB于E,
∵DC∥AB,DA⊥AB,
∴四边形AECD是矩形,
∴AE=CD=5,CE=AD=4,
∴BE=3,
∴BC=,
∴BC<AB,
∴P到C时,P、Q同时停止运动,
∴t=(秒),
即t=5秒时,P,Q两点同时停止运动.
(2)由题意知,AQ=BP=t,
∴QB=8﹣t,
作PF⊥QB于F,则△BPF~△BCE,
∴,即,
∴BF=,
∴S=QB PF=×(8﹣t)==﹣(t﹣4)2+(0<t≤5),
∵﹣<0,
∴S有最大值,当t=4时,S的最大值是;
(3)∵cos∠B=,
①当PQ=PB时(如图2所示),则BG=BQ,
==,解得t=s,
②当PQ=BQ时(如图3所示),则BG=PB,
==,解得t=s,
③当BP=BQ时(如图4所示),则8﹣t=t,
解得:t=4.
综上所述:当t=s,
s或t=4s时,△PQB为等腰三角形.
2016年11月23日
第6页(共20页)
同课章节目录
