八年级上册14.1《直角三角形三边的关系》专题练习题含答案
文档属性
| 名称 | 八年级上册14.1《直角三角形三边的关系》专题练习题含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 193.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-06 00:00:00 | ||
图片预览

文档简介
华东师大版数学八年级上册
第14章
勾股定理直角三角形三边的关系
专题练习题
1.如图,在边长为1个单位长度的小正方形组成的网格中,点A,B都是格点,则线段AB的长度为( )
A.5
B.6
C.7
D.25
2.在Rt△ABC中,斜边BC=8
cm,则AB2+BC2+AC2等于( )
A.64
cm2
B.96
cm2
C.128
cm2
D.144
cm2
3.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,
(1)若a=3
cm,c=5
cm,则b=________;
(2)若a=5
cm,b=12
cm,则c=________;
(3)若a∶b=3∶4,c=10
cm,则a=________,b=________.
4.如图,在等腰△ABC中,AB=AC,AD是底边上的高,若AB=5
cm,BC=6
cm,则AD=________cm.
5.如图,三个正方形中的两个的面积S1=25,S2=144,则另一个的面积S3为________.
6.求出下列直角三角形中未知边AB的长度.
7.如图,在Rt△ABC中,∠C=90°,AB=15
cm,则两个正方形面积的和为( )
A.150
cm2
B.200
cm2
C.225
cm2
D.350
cm2
8.如图,矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为( )
A.14
B.16
C.20
D.28
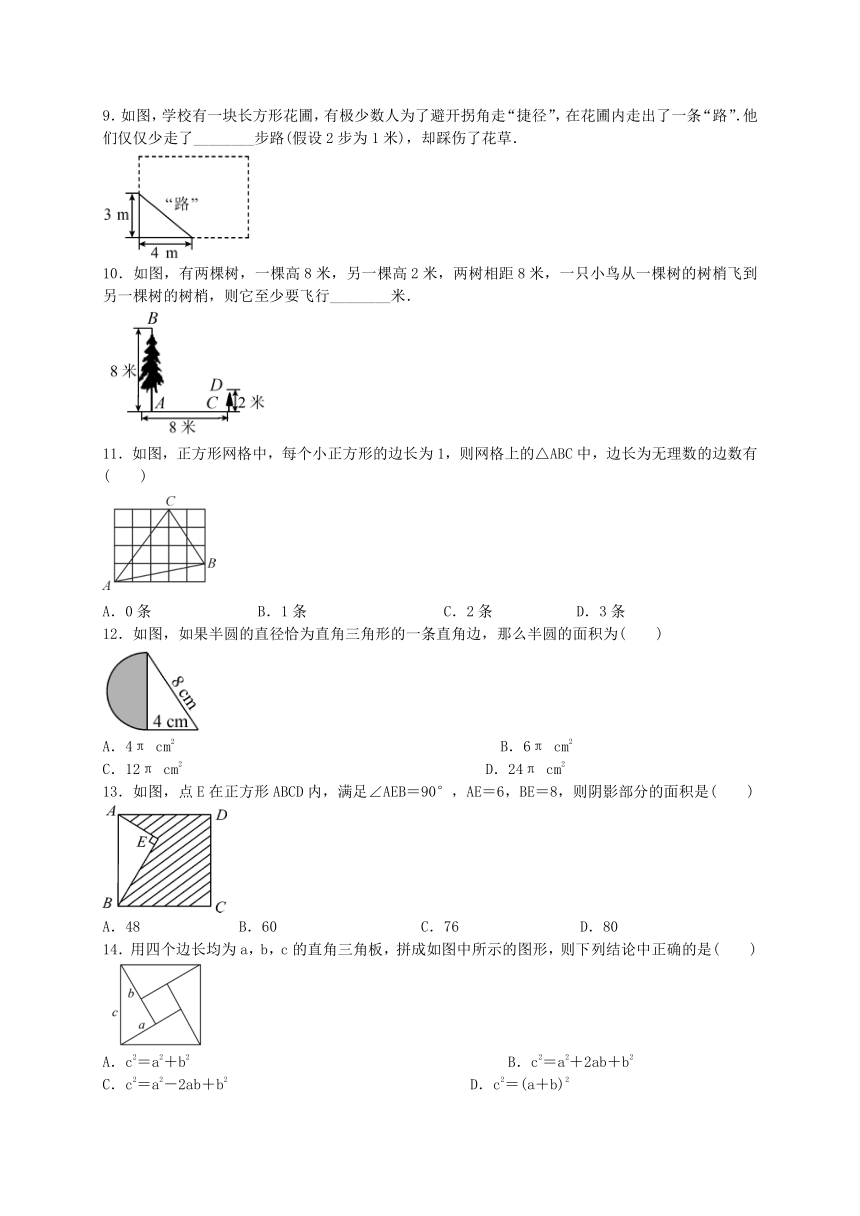
9.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了________步路(假设2步为1米),却踩伤了花草.
10.如图,有两棵树,一棵高8米,另一棵高2米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,则它至少要飞行________米.
11.如图,正方形网格中,每个小正方形的边长为1,则网格上的△ABC中,边长为无理数的边数有( )
A.0条
B.1条
C.2条
D.3条
12.如图,如果半圆的直径恰为直角三角形的一条直角边,那么半圆的面积为( )
A.4π
cm2
B.6π
cm2
C.12π
cm2
D.24π
cm2
13.如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A.48
B.60
C.76
D.80
14.用四个边长均为a,b,c的直角三角板,拼成如图中所示的图形,则下列结论中正确的是( )
A.c2=a2+b2
B.c2=a2+2ab+b2
C.c2=a2-2ab+b2
D.c2=(a+b)2
15.如图,在Rt△ABC中,∠B=90°,沿AD折叠,使点B落在斜边AC上,若AB=3,BC=4,则BD=________.
16.如图,在锐角△ABC中,高AD=12,边AC=13,BC=14,求AB的长.
17.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.
(1)求DE的长;
(2)求△ADB的面积.
18.如图,折叠长方形的一边AD,使点D落在BC边的点F处,且AB=8
cm,BC=10
cm,求EC的长.
19.一架云梯长25米,如图斜靠在一面墙上,梯子底端离墙7米.
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米,
那么梯子的底部在水平方向也滑动了4米吗?
答案:
1.
A
2.
C
3.
(1)
4cm
(2)
13cm
(3)
6cm
8cm
4.
4
5.
169
6.
(1)AB=16
(2)AB=25
7.
C
8.
D
9.
4
10.
10
11.
C
12.
B
13.
C
14.
A
15.
16.
在Rt△ADC中,CD===5,∴BD=BC-CD=14-5=9,∴AB===15
17.
(1)∵AD平分∠CAB,DE⊥AB,∠C=90°,∴CD=DE,∵CD=3,∴DE=3
(2)在Rt△ABC中,由勾股定理得:AB===10,∴△ADB的面积为S△ADB=AB·DE=×10×3=15
18.
∵D,F关于AE对称,∴△AFE≌△ADE,∴AF=AD=BC=10,DE=EF,设EC=x,则DE=8-x,在Rt△ABF中,BF==[JP]6,∴FC=BC-BF=4,在Rt△CEF中,EF2=EC2+FC2,∴(8-x)2=x2+42,解得x=3,
即EC的长为3
cm
19.
(1)设这个梯子的顶端距地面有x米高,据题意得AB2+BC2=AC2,即x2+72=252,解得x=24.
即这个梯子的顶端距地面有24米高
(2)如果梯子的顶端下滑了4米,即AD=4米,BD=20米,设梯子底端离墙距离为y米,据题意得BD2+BE2=DE2,即202+y2=252,解得y=15,此时CE=15-7=8,即梯子的底部在水平方向滑动了8米
第14章
勾股定理直角三角形三边的关系
专题练习题
1.如图,在边长为1个单位长度的小正方形组成的网格中,点A,B都是格点,则线段AB的长度为( )
A.5
B.6
C.7
D.25
2.在Rt△ABC中,斜边BC=8
cm,则AB2+BC2+AC2等于( )
A.64
cm2
B.96
cm2
C.128
cm2
D.144
cm2
3.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,
(1)若a=3
cm,c=5
cm,则b=________;
(2)若a=5
cm,b=12
cm,则c=________;
(3)若a∶b=3∶4,c=10
cm,则a=________,b=________.
4.如图,在等腰△ABC中,AB=AC,AD是底边上的高,若AB=5
cm,BC=6
cm,则AD=________cm.
5.如图,三个正方形中的两个的面积S1=25,S2=144,则另一个的面积S3为________.
6.求出下列直角三角形中未知边AB的长度.
7.如图,在Rt△ABC中,∠C=90°,AB=15
cm,则两个正方形面积的和为( )
A.150
cm2
B.200
cm2
C.225
cm2
D.350
cm2
8.如图,矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为( )
A.14
B.16
C.20
D.28
9.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了________步路(假设2步为1米),却踩伤了花草.
10.如图,有两棵树,一棵高8米,另一棵高2米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,则它至少要飞行________米.
11.如图,正方形网格中,每个小正方形的边长为1,则网格上的△ABC中,边长为无理数的边数有( )
A.0条
B.1条
C.2条
D.3条
12.如图,如果半圆的直径恰为直角三角形的一条直角边,那么半圆的面积为( )
A.4π
cm2
B.6π
cm2
C.12π
cm2
D.24π
cm2
13.如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A.48
B.60
C.76
D.80
14.用四个边长均为a,b,c的直角三角板,拼成如图中所示的图形,则下列结论中正确的是( )
A.c2=a2+b2
B.c2=a2+2ab+b2
C.c2=a2-2ab+b2
D.c2=(a+b)2
15.如图,在Rt△ABC中,∠B=90°,沿AD折叠,使点B落在斜边AC上,若AB=3,BC=4,则BD=________.
16.如图,在锐角△ABC中,高AD=12,边AC=13,BC=14,求AB的长.
17.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.
(1)求DE的长;
(2)求△ADB的面积.
18.如图,折叠长方形的一边AD,使点D落在BC边的点F处,且AB=8
cm,BC=10
cm,求EC的长.
19.一架云梯长25米,如图斜靠在一面墙上,梯子底端离墙7米.
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米,
那么梯子的底部在水平方向也滑动了4米吗?
答案:
1.
A
2.
C
3.
(1)
4cm
(2)
13cm
(3)
6cm
8cm
4.
4
5.
169
6.
(1)AB=16
(2)AB=25
7.
C
8.
D
9.
4
10.
10
11.
C
12.
B
13.
C
14.
A
15.
16.
在Rt△ADC中,CD===5,∴BD=BC-CD=14-5=9,∴AB===15
17.
(1)∵AD平分∠CAB,DE⊥AB,∠C=90°,∴CD=DE,∵CD=3,∴DE=3
(2)在Rt△ABC中,由勾股定理得:AB===10,∴△ADB的面积为S△ADB=AB·DE=×10×3=15
18.
∵D,F关于AE对称,∴△AFE≌△ADE,∴AF=AD=BC=10,DE=EF,设EC=x,则DE=8-x,在Rt△ABF中,BF==[JP]6,∴FC=BC-BF=4,在Rt△CEF中,EF2=EC2+FC2,∴(8-x)2=x2+42,解得x=3,
即EC的长为3
cm
19.
(1)设这个梯子的顶端距地面有x米高,据题意得AB2+BC2=AC2,即x2+72=252,解得x=24.
即这个梯子的顶端距地面有24米高
(2)如果梯子的顶端下滑了4米,即AD=4米,BD=20米,设梯子底端离墙距离为y米,据题意得BD2+BE2=DE2,即202+y2=252,解得y=15,此时CE=15-7=8,即梯子的底部在水平方向滑动了8米
