2.1 数列的概念与简单表示法 课件1
文档属性
| 名称 | 2.1 数列的概念与简单表示法 课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-08 00:00:00 | ||
图片预览





文档简介
课件17张PPT。 第二章 数列
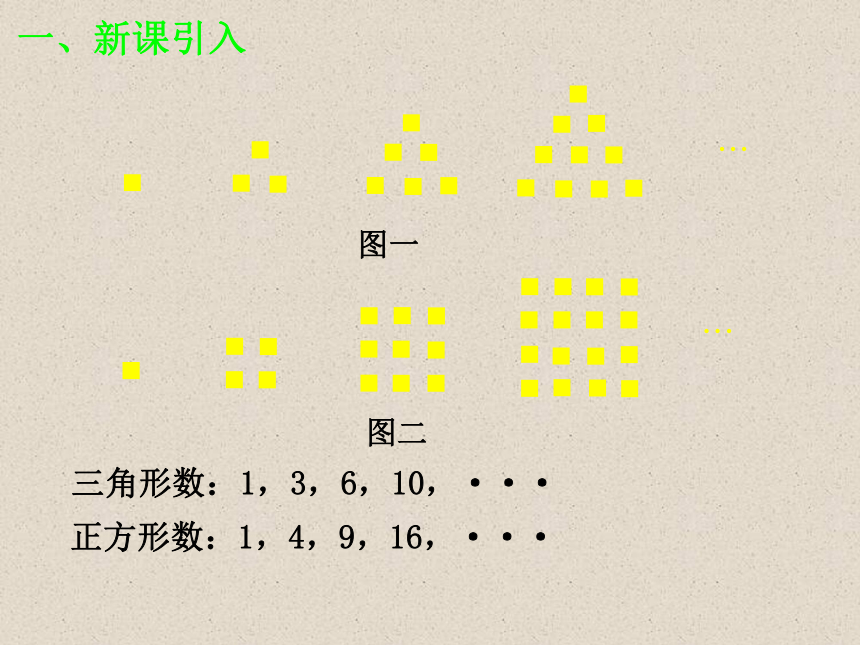
2.1 数列的概念与简单表示法正方形数:1,4,9,16,·········三角形数:1,3,6,10,···图一图二一、新课引入二、新课讲解1. 定义:按一定顺序排列着的一列数称为数列的特征:有序性数列思考: 数列-1,1,-1,1……改为1,-1,1,-1……,
请问:是不是同一数列?数列的一般形式可以写成:简记为{an}2.数列中的每一个数叫做这个数列的项。各项依次叫做这个数列的首项,第2项,···,第n项, ···不是二、新课讲解3.数列的分类(1)按项数分:项数有限的数列叫有穷数列项数无限的数列叫无穷数列(2)按项之间的大小关系:递增数列,递减数列,摆动数列,常数列。二、新课讲解(1) 全体自然数构成的数列:0,1,2,3,…(2) 无穷多个3构成的数列:3,3,3,3,…(3) 人民币面额(单位:元)按一定顺序构成的数列:
100,50,20,10,5,2,1,0.5,0.2,0.1,0.05,0.02,0.01.(4) -1的1次幂,2次幂,3次幂,4次幂…构成的数列:
-1,1,-1,1, …练习: 判断下列数列是属于哪类数列.答案:
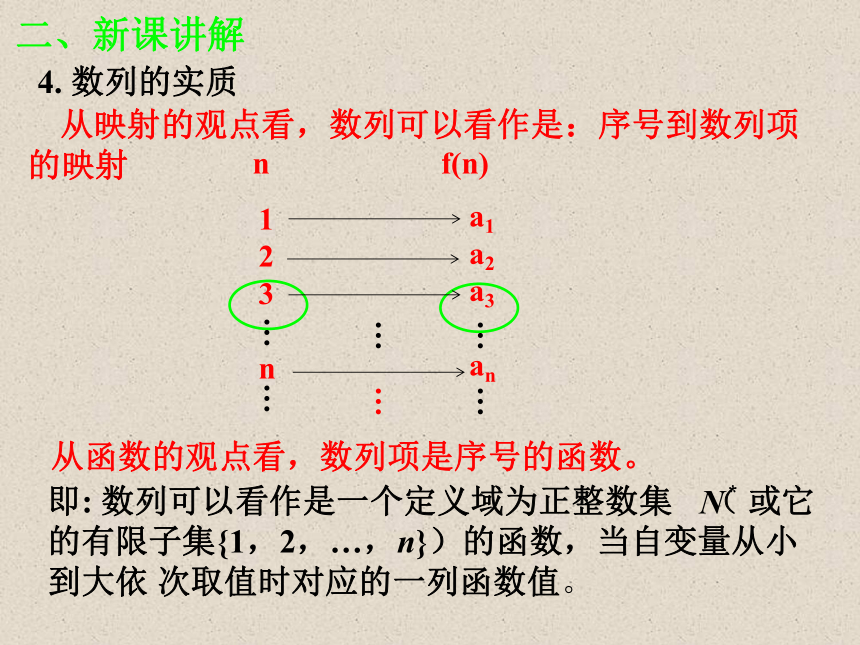
1.递增数列 2.常数列 3.递减数列 4.摆动数列 从映射的观点看,数列可以看作是:序号到数列项的映射4. 数列的实质即: 数列可以看作是一个定义域为正整数集 ( 或它的有限子集{1,2,…,n})的函数,当自变量从小到大依 次取值时对应的一列函数值。 从函数的观点看,数列项是序号的函数。二、新课讲解5. 数列的项an与项数n的关系如果数列{an}的第n项an与序号n之间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的通项公式. 二、新课讲解例1.根据下列数列的前几项的值,写出数列的一个通项公式: 答案:二、新课讲解请思考:根据数列的前若干项写出的通项公式的形式唯一吗?①一些数列的通项公式不是唯一的②不是每一个数列都能写出它的通项公式③数列的通项公式不一定是一个式子,也可以是分段
函数. 二、新课讲解6. 数列的表示法列表法以数列: 2, 4, 6, 8, 10, 12, · · · 为例通项公式法: 图象法(见下一页)an=2n递推法an= an-1 +2a1= 2(n>1)二、新课讲解图象法为:an
10
9
8
7
6
5
4
3
2 0 1 2 3 4 5 n图象为直线
上的无数个
孤立点例2.下图中的三角形称为谢宾斯基三角形,在下图4个
三角形中,着色三角形的个数依次构成一个数列的前
4项,请写出这个数列的一个通项公式,并在直角坐标
系中画出它的图象.二、新课讲解an
30
27
24
21
18
15
12
9
6
3
o 1 2 3 4 5 n图象为曲线上的无数个孤立点观察:1,3,9,27这些数有什么规律吗?首项为1,从第2项起每一项等于它的前一项的2
倍再加1,即an=2an-1+1(n>1)二、新课讲解解:∵a1=1二、新课讲解写出下列数列{an}的前5项
(1)a1=5,an=an-1+3 (n≥2);
(2)a1=2,an=2an-1 (n≥2);(1)5,8,11,14,17
(2)2,4,8,16,32三、练习思考:你能否利用上面两题的条件求出数列{an}的
通项公式?(1)后一项比前一项多3分析(2)后一项是前一项的2倍
2.1 数列的概念与简单表示法正方形数:1,4,9,16,·········三角形数:1,3,6,10,···图一图二一、新课引入二、新课讲解1. 定义:按一定顺序排列着的一列数称为数列的特征:有序性数列思考: 数列-1,1,-1,1……改为1,-1,1,-1……,
请问:是不是同一数列?数列的一般形式可以写成:简记为{an}2.数列中的每一个数叫做这个数列的项。各项依次叫做这个数列的首项,第2项,···,第n项, ···不是二、新课讲解3.数列的分类(1)按项数分:项数有限的数列叫有穷数列项数无限的数列叫无穷数列(2)按项之间的大小关系:递增数列,递减数列,摆动数列,常数列。二、新课讲解(1) 全体自然数构成的数列:0,1,2,3,…(2) 无穷多个3构成的数列:3,3,3,3,…(3) 人民币面额(单位:元)按一定顺序构成的数列:
100,50,20,10,5,2,1,0.5,0.2,0.1,0.05,0.02,0.01.(4) -1的1次幂,2次幂,3次幂,4次幂…构成的数列:
-1,1,-1,1, …练习: 判断下列数列是属于哪类数列.答案:
1.递增数列 2.常数列 3.递减数列 4.摆动数列 从映射的观点看,数列可以看作是:序号到数列项的映射4. 数列的实质即: 数列可以看作是一个定义域为正整数集 ( 或它的有限子集{1,2,…,n})的函数,当自变量从小到大依 次取值时对应的一列函数值。 从函数的观点看,数列项是序号的函数。二、新课讲解5. 数列的项an与项数n的关系如果数列{an}的第n项an与序号n之间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的通项公式. 二、新课讲解例1.根据下列数列的前几项的值,写出数列的一个通项公式: 答案:二、新课讲解请思考:根据数列的前若干项写出的通项公式的形式唯一吗?①一些数列的通项公式不是唯一的②不是每一个数列都能写出它的通项公式③数列的通项公式不一定是一个式子,也可以是分段
函数. 二、新课讲解6. 数列的表示法列表法以数列: 2, 4, 6, 8, 10, 12, · · · 为例通项公式法: 图象法(见下一页)an=2n递推法an= an-1 +2a1= 2(n>1)二、新课讲解图象法为:an
10
9
8
7
6
5
4
3
2 0 1 2 3 4 5 n图象为直线
上的无数个
孤立点例2.下图中的三角形称为谢宾斯基三角形,在下图4个
三角形中,着色三角形的个数依次构成一个数列的前
4项,请写出这个数列的一个通项公式,并在直角坐标
系中画出它的图象.二、新课讲解an
30
27
24
21
18
15
12
9
6
3
o 1 2 3 4 5 n图象为曲线上的无数个孤立点观察:1,3,9,27这些数有什么规律吗?首项为1,从第2项起每一项等于它的前一项的2
倍再加1,即an=2an-1+1(n>1)二、新课讲解解:∵a1=1二、新课讲解写出下列数列{an}的前5项
(1)a1=5,an=an-1+3 (n≥2);
(2)a1=2,an=2an-1 (n≥2);(1)5,8,11,14,17
(2)2,4,8,16,32三、练习思考:你能否利用上面两题的条件求出数列{an}的
通项公式?(1)后一项比前一项多3分析(2)后一项是前一项的2倍
