2.1 数列的概念与简单表示法 课件2
文档属性
| 名称 | 2.1 数列的概念与简单表示法 课件2 |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-08 09:30:08 | ||
图片预览







文档简介
课件23张PPT。 第二章 数列
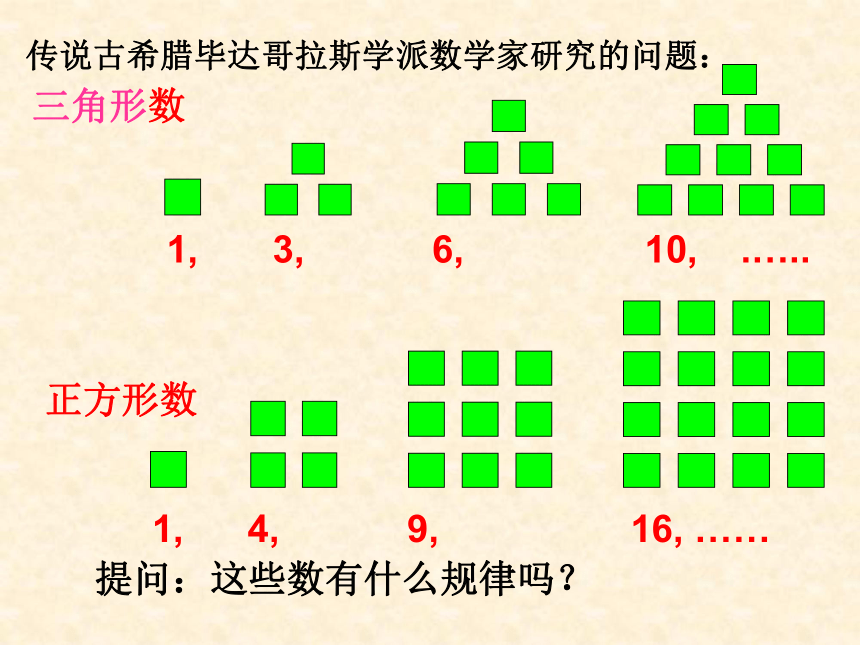
2.1 数列的概念与简单表示法64个格子1223344551667788OK456781567812334264个格子你认为国王有能力满足上述要求吗每个格子里的麦粒数都是前一个格子里麦粒数的2倍且共有64格子麦粒总数???18446744073709551615三角形数1, 3, 6, 10, .….. 正方形数1, 4, 9, 16, ……传说古希腊毕达哥拉斯学派数学家研究的问题:提问:这些数有什么规律吗?上述棋盘中各格子里的麦粒数按先后次序排成一列数:1,2,3,4……的倒数排列成的一列数:高一(5)班每次考试的名次由小到大排成的一列数:-1的1次幂,2次幂,3次幂,……排列成一列数:无穷多个1排列成的一列数:三角形数:1,3,6,10,···正方形数:1,4,9,16,···请
观
察?共同特点:1. 都是一列数;2. 都有一定的顺序1,3,6,10,···1,4,9,16,···定义:按一定顺序排列着的一列数称为数列问1:数列 ,2 , 改为13 ,… ,35 , 2 , ,… ,3531请问:是不是同一数列?问2:数列改为:-1,1,-1,1……1,-1,1,-1……,请问:是不是同一数列?不是不是(数列具有有序性)1想一想:数列与集合的区别是什么?
(1)数列{an}中是一列数,而集合中的元素不一定是数;
(2) 数列{an}中的数是有一定次序的,而集合中的元素没有次序;
(3) 数列{an}中的数可以重复,而集合中的元素不能重复。思考:数列与集合的概念有何区别2数列中的每一个数叫做这个数列的项。各项依次叫做这个数列的第1项,第2项,······,第n项, ······
3数列的分类(1)按项数分:项数有限的数列叫有穷数列项数无限的数列叫无穷数列(2)按项之间的大小关系:递增数列,递减数列,摆动数列,常数列。有穷数列无穷数列有穷数列无穷数列无穷数列递增数列递增数列递减数列摆动数列常数列4 数列的一般形式可以
写成:简记为 其中是数第1项第2项第3项第n项5 的第n项
与项数之间的关系可以用一个公式来表示,列的第n项。??? 那么这个公式就叫做这个数列的通项公式。如果数列或??思 考 :根据数列的前若干项写出的通项公式的形式唯一吗?请举例说明。? 例1:写出下面数列的一个通项公式,使它的前4项分别是下列各数:注意:①一些数列的通项公式不是唯一的②不是每一个数列都能写出它的通项公式③ 对于数列中的每个序号n,都有唯一的一个数(项)an与之对应.序号n 1 2 3 4 ……64
项an 1 2 22 23 …… 263
(自变量)(函数值)数列是一种特殊的函数可以认为:数列与函数的关系:6 从函数的观点看, 是 的函数。
数列的项序号 数列可以看作是一个定义域为正整数集 N* ( 或它的有限子集{1,2,…,n})的函数, ,即当自变量从小到大依次取值时对应的一列函数值。数列的通项公式也就是相应函数的解析式例 设某一数列的通项公式为高一(2)班考试名次由小到大排成的一列数例每个序号也都对应着一个数(项)序号项 从函数的观点看,
是 的函数。
y=f(x)ann函数值自变量 从映射的观点看,数列可以看作是: 到 的映射数列项
序号数列项序号 (正整数或它的有限子集)项7数列的实质序号项即,数列可以看作是一个定义域为正整数集
( 或它的有限子集{1,2,…,n})的函数,当自变量从小到大依 次取值时对应的一列函数值。序号通项公式
1
2
2.5
4
4.5
3
4
5
6
7a1
a2
a3
a4
a5
1
2
3
4
5xynan通项公式:数列{an}的第n项an与n的关系式数列是一种特殊函数!定义域是N*(或它的有限子集) 对于数列中的每个序号n都有唯一的一个数(项)an与之对应.项数n 1 2 3 4 ……64
项an 1 2 22 23 …… 263
(自变量n)(函数值an )数列与函数数列是一种特殊的函数可以认为:1234567891024681012141618200是些孤立点-1我们好孤单!我们好孤单!数列的图像是相应的曲线(或直线)
上横坐标为正整数的一群孤立的点。例2. 下图中的三角形称为谢宾斯基三角形,在下图4个三角形中,着色三角形的个数依次构成一个数列的前
4项,请写出这个数列的一个通项公式,并在直角坐标
系中画出它的图象.8数列用图象表示时的特点——一群孤立的点递推公式:递推公式也是数列的一种表示方法。解:∵a1=1 1.通项公式能够很清楚的表示数列中项数和项的关系;数列的通项公式有什么用呢?2.由通项公式可以求出数列中的每一项.例: 根据下面数列的通项公式,写出前5项.例、 写出下面数列的一个通项公式,使它的 前4项分别是下列各数:
2.1 数列的概念与简单表示法64个格子1223344551667788OK456781567812334264个格子你认为国王有能力满足上述要求吗每个格子里的麦粒数都是前一个格子里麦粒数的2倍且共有64格子麦粒总数???18446744073709551615三角形数1, 3, 6, 10, .….. 正方形数1, 4, 9, 16, ……传说古希腊毕达哥拉斯学派数学家研究的问题:提问:这些数有什么规律吗?上述棋盘中各格子里的麦粒数按先后次序排成一列数:1,2,3,4……的倒数排列成的一列数:高一(5)班每次考试的名次由小到大排成的一列数:-1的1次幂,2次幂,3次幂,……排列成一列数:无穷多个1排列成的一列数:三角形数:1,3,6,10,···正方形数:1,4,9,16,···请
观
察?共同特点:1. 都是一列数;2. 都有一定的顺序1,3,6,10,···1,4,9,16,···定义:按一定顺序排列着的一列数称为数列问1:数列 ,2 , 改为13 ,… ,35 , 2 , ,… ,3531请问:是不是同一数列?问2:数列改为:-1,1,-1,1……1,-1,1,-1……,请问:是不是同一数列?不是不是(数列具有有序性)1想一想:数列与集合的区别是什么?
(1)数列{an}中是一列数,而集合中的元素不一定是数;
(2) 数列{an}中的数是有一定次序的,而集合中的元素没有次序;
(3) 数列{an}中的数可以重复,而集合中的元素不能重复。思考:数列与集合的概念有何区别2数列中的每一个数叫做这个数列的项。各项依次叫做这个数列的第1项,第2项,······,第n项, ······
3数列的分类(1)按项数分:项数有限的数列叫有穷数列项数无限的数列叫无穷数列(2)按项之间的大小关系:递增数列,递减数列,摆动数列,常数列。有穷数列无穷数列有穷数列无穷数列无穷数列递增数列递增数列递减数列摆动数列常数列4 数列的一般形式可以
写成:简记为 其中是数第1项第2项第3项第n项5 的第n项
与项数之间的关系可以用一个公式来表示,列的第n项。??? 那么这个公式就叫做这个数列的通项公式。如果数列或??思 考 :根据数列的前若干项写出的通项公式的形式唯一吗?请举例说明。? 例1:写出下面数列的一个通项公式,使它的前4项分别是下列各数:注意:①一些数列的通项公式不是唯一的②不是每一个数列都能写出它的通项公式③ 对于数列中的每个序号n,都有唯一的一个数(项)an与之对应.序号n 1 2 3 4 ……64
项an 1 2 22 23 …… 263
(自变量)(函数值)数列是一种特殊的函数可以认为:数列与函数的关系:6 从函数的观点看, 是 的函数。
数列的项序号 数列可以看作是一个定义域为正整数集 N* ( 或它的有限子集{1,2,…,n})的函数, ,即当自变量从小到大依次取值时对应的一列函数值。数列的通项公式也就是相应函数的解析式例 设某一数列的通项公式为高一(2)班考试名次由小到大排成的一列数例每个序号也都对应着一个数(项)序号项 从函数的观点看,
是 的函数。
y=f(x)ann函数值自变量 从映射的观点看,数列可以看作是: 到 的映射数列项
序号数列项序号 (正整数或它的有限子集)项7数列的实质序号项即,数列可以看作是一个定义域为正整数集
( 或它的有限子集{1,2,…,n})的函数,当自变量从小到大依 次取值时对应的一列函数值。序号通项公式
1
2
2.5
4
4.5
3
4
5
6
7a1
a2
a3
a4
a5
1
2
3
4
5xynan通项公式:数列{an}的第n项an与n的关系式数列是一种特殊函数!定义域是N*(或它的有限子集) 对于数列中的每个序号n都有唯一的一个数(项)an与之对应.项数n 1 2 3 4 ……64
项an 1 2 22 23 …… 263
(自变量n)(函数值an )数列与函数数列是一种特殊的函数可以认为:1234567891024681012141618200是些孤立点-1我们好孤单!我们好孤单!数列的图像是相应的曲线(或直线)
上横坐标为正整数的一群孤立的点。例2. 下图中的三角形称为谢宾斯基三角形,在下图4个三角形中,着色三角形的个数依次构成一个数列的前
4项,请写出这个数列的一个通项公式,并在直角坐标
系中画出它的图象.8数列用图象表示时的特点——一群孤立的点递推公式:递推公式也是数列的一种表示方法。解:∵a1=1 1.通项公式能够很清楚的表示数列中项数和项的关系;数列的通项公式有什么用呢?2.由通项公式可以求出数列中的每一项.例: 根据下面数列的通项公式,写出前5项.例、 写出下面数列的一个通项公式,使它的 前4项分别是下列各数:
