2.4 等比数列 课件4
图片预览






文档简介
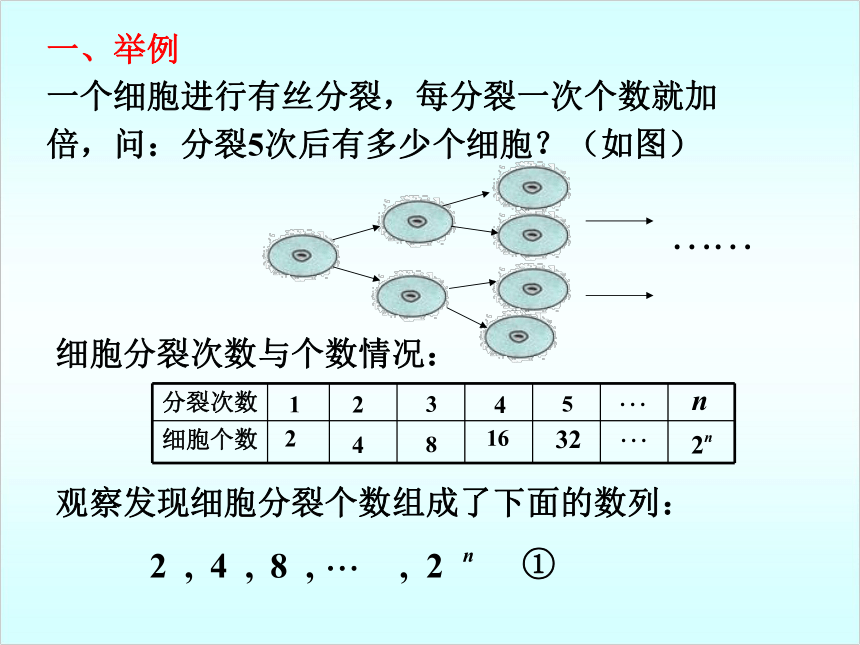
课件17张PPT。2.4等比数列 一个细胞进行有丝分裂,每分裂一次个数就加倍,问:分裂5次后有多少个细胞?(如图)观察发现细胞分裂个数组成了下面的数列:细胞分裂次数与个数情况:一、举例
①庄子曰:“一尺之棰,日取其半,万世不竭.”意思:“一尺长的木棒,每日取其一半,永远也取不完.” 如果将“一尺之棰”视为一份,则每 日剩下的部分依次为:这两数列的特点:从第2项起,每一项与前一项的比都等于同一常数.结合例1得到的数列观察:我们把这样的数列称为等比数列.②① ①若 q=0,根据定义 则 ,那么对 ,则出现分母为0,无意义.故q≠0 二、探究
1、等比数列定义:
一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫等比数列的公比,用字母q表示(q≠0) ②若存在 ,根据定义 ,则分母出现0,无意义,故一切项都不能为0.注:等比数列的公比和任意一项都不能为0. 用符号语言表示:在数列 中,若 则 是等比数列
例1.①已知数列 的通向公式为 ,试问这个数列是等比数列吗?说明理由. ②若 呢?②这个数列不是等比数列解:①这个数列是等比数列,以下证明:所以,这个数列不是等比数列.所以,数列是以公比为2的等比数列.是常数注:①证明一个数列是等比数列应从定义入手 ②证明一个数列不是等比数列,只需举出三项不成等比即可.如果a与b之间插入一个数G ,使a,G,b成等比数列,那么G叫做a与b 的等比中项.2.等比中项 注:(1)等比中项G有两个;根据等比数列的定义有(2)因为 ,故a与b必须同号;(3)若去掉 a≠0,b≠0且G≠0,则由 得不到a,G,b成等比数列.3.通项公式 首项是 ,公比是 的等比数列 的通项公式为:①推导:方法一(不完全归纳法)归纳得到: 方法二把以上(n-1)个式子左右相乘:因为当n=1时 也满足上式的结论(叠乘法)12345678910246810121416180●●●●数列 的图像是函数 的图像上的孤立点.即数列 中的各项是函数 的图像上的孤立点的纵坐标.数列 的图像是函数 的图像上的孤立点.一般性结论:例2.已知等比数列 中, 求③方程思想: 中有四个量首项 ,公比q ,项数n,末项 ,要能知三求一.解:(1)定义法:4、判断一个数列是等比数列的方法归纳:(2)等比中项法:(3)通项公式法:注:证明一个数列是等比数列要用定义证明 5、性质:等比数列 首项 ,公比 (1)广义通项公式:证明:例3.等比数列 中, 则公比q是多少?解法一:应用广义通项公式解法二:化成含有 和q的式子,解方程组三、课堂小结 3、等比数列的通项公式及其推导方法,特别是叠乘法要求掌握;4、判断等比数列的方法: (1)定义法;(2)等比中项公式法;(3)通向公式.2、等比中项的定义及应用;1、等比数列的定义及证明等比数列的方法:必须用定义证明谢谢观看!
1、等比数列定义:
一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫等比数列的公比,用字母q表示(q≠0) ②若存在 ,根据定义 ,则分母出现0,无意义,故一切项都不能为0.注:等比数列的公比和任意一项都不能为0. 用符号语言表示:在数列 中,若 则 是等比数列
例1.①已知数列 的通向公式为 ,试问这个数列是等比数列吗?说明理由. ②若 呢?②这个数列不是等比数列解:①这个数列是等比数列,以下证明:所以,这个数列不是等比数列.所以,数列是以公比为2的等比数列.是常数注:①证明一个数列是等比数列应从定义入手 ②证明一个数列不是等比数列,只需举出三项不成等比即可.如果a与b之间插入一个数G ,使a,G,b成等比数列,那么G叫做a与b 的等比中项.2.等比中项 注:(1)等比中项G有两个;根据等比数列的定义有(2)因为 ,故a与b必须同号;(3)若去掉 a≠0,b≠0且G≠0,则由 得不到a,G,b成等比数列.3.通项公式 首项是 ,公比是 的等比数列 的通项公式为:①推导:方法一(不完全归纳法)归纳得到: 方法二把以上(n-1)个式子左右相乘:因为当n=1时 也满足上式的结论(叠乘法)12345678910246810121416180●●●●数列 的图像是函数 的图像上的孤立点.即数列 中的各项是函数 的图像上的孤立点的纵坐标.数列 的图像是函数 的图像上的孤立点.一般性结论:例2.已知等比数列 中, 求③方程思想: 中有四个量首项 ,公比q ,项数n,末项 ,要能知三求一.解:(1)定义法:4、判断一个数列是等比数列的方法归纳:(2)等比中项法:(3)通项公式法:注:证明一个数列是等比数列要用定义证明 5、性质:等比数列 首项 ,公比 (1)广义通项公式:证明:例3.等比数列 中, 则公比q是多少?解法一:应用广义通项公式解法二:化成含有 和q的式子,解方程组三、课堂小结 3、等比数列的通项公式及其推导方法,特别是叠乘法要求掌握;4、判断等比数列的方法: (1)定义法;(2)等比中项公式法;(3)通向公式.2、等比中项的定义及应用;1、等比数列的定义及证明等比数列的方法:必须用定义证明谢谢观看!
