第三章 三角恒等变换单元综合检测题二(带解析)
文档属性
| 名称 | 第三章 三角恒等变换单元综合检测题二(带解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 793.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-08 00:00:00 | ||
图片预览

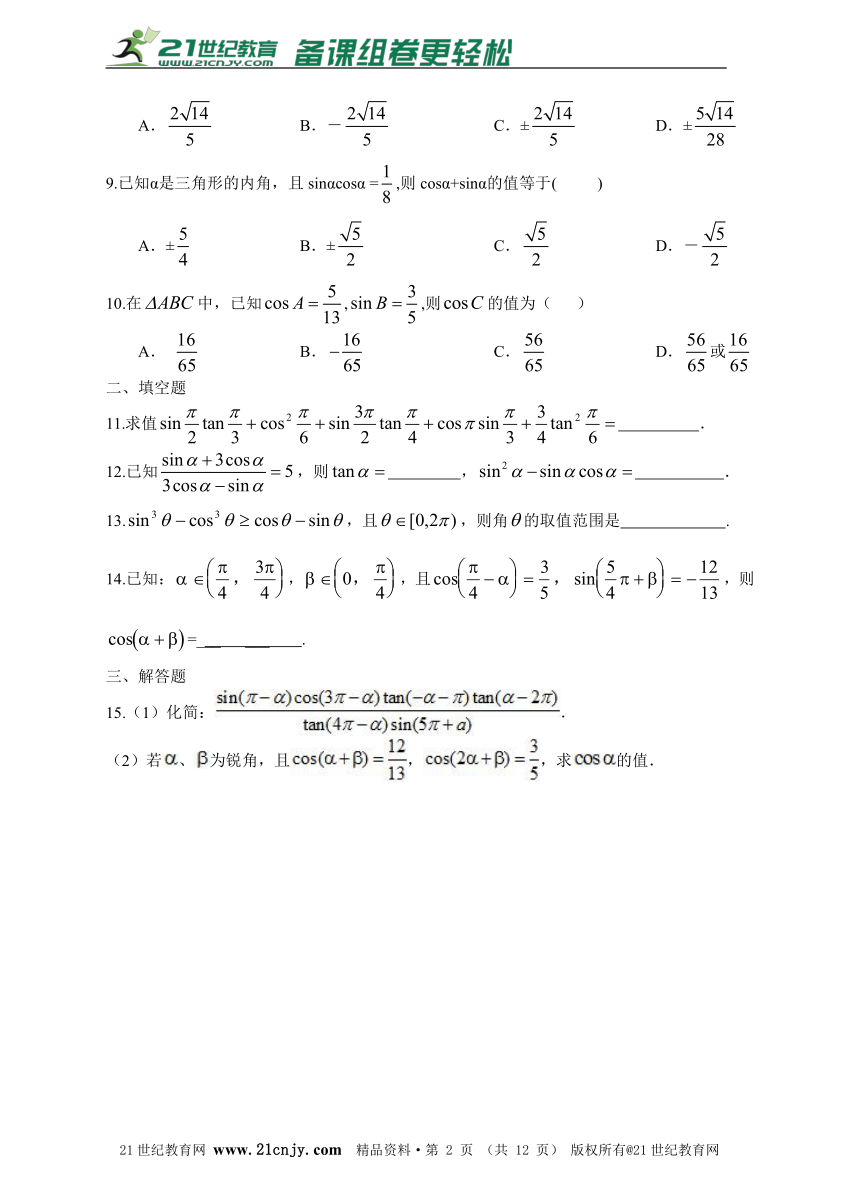


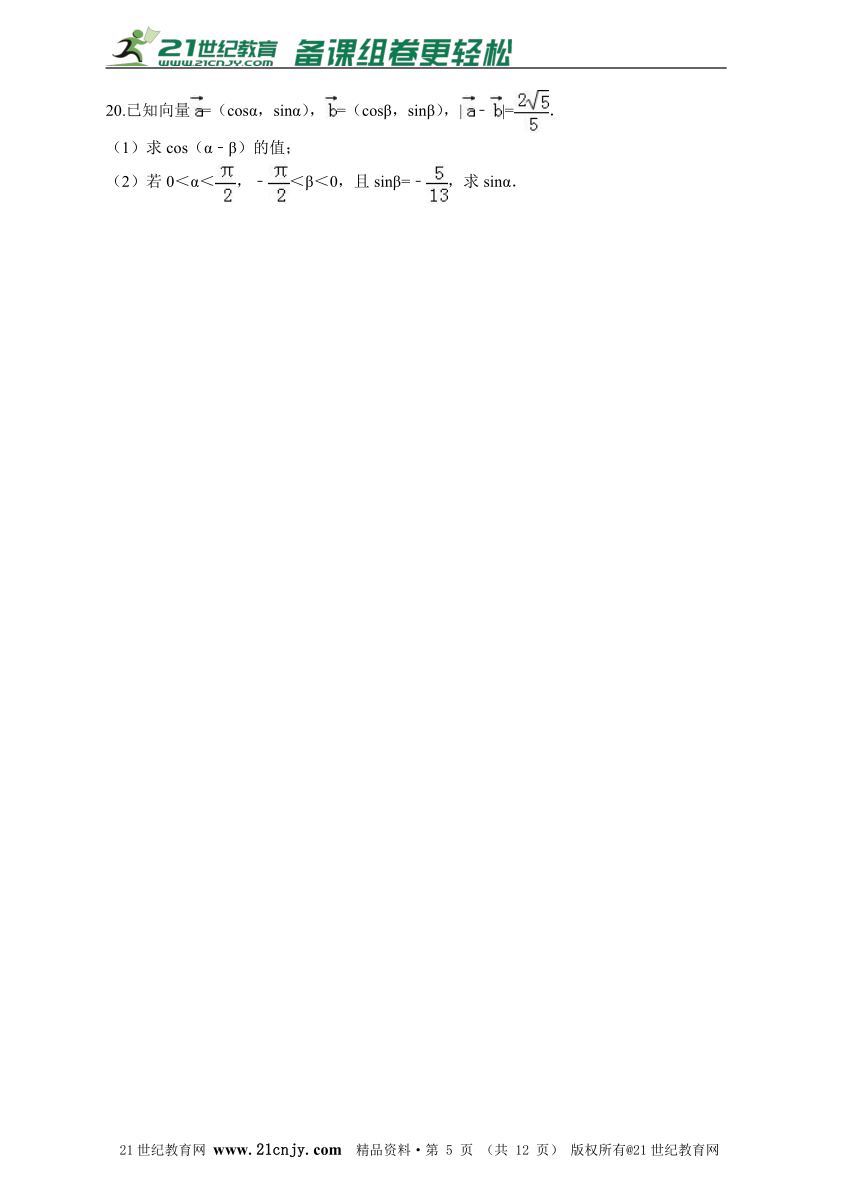
文档简介
第三章 三角恒等变换单元综合检测题二(带解析)
一、选择题
1.化简的结果是( )
A.1 B. C.2 D.
2.化简( )
A. B. C. D.
3.已知,,则是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
4.(α+β)=,tan=,那么tan等于( )
A. B. C. D.
5.在中,,则( )
A. B. C.2 D.
6.函数是( )
A.最小正周期为的奇函数 B.最小正周期为的奇函数
C.最小正周期为的偶函数 D.最小正周期为的偶函数
7.已知角的顶点与原点重合,始边与轴的正半轴重合,终边在直线上,则( )
A. B. C. D.
8.已知,,且为锐角,则( )
A. B.- C.± D.±
9.已知α是三角形的内角,且sinαcosα =,则cosα+sinα的值等于( )
A.± B.± C. D.-
10.在中,已知,,则的值为( )
A. B. C. D.或
二、填空题
11.求值 .
12.已知,则 , .
13.,且,则角的取值范围是 .
14.已知:,,且,则=___ ___ .
三、解答题
15.(1)化简:.
(2)若、为锐角,且,,求的值.
16.已知tanα是关于x的方程的一个实根,且α是第三象限角.
(1)求的值;
(2)求的值.
17.已知函数
(Ⅰ)求该函数的周期和最大值;
(Ⅱ)该函数的图象经过怎样的平移和伸缩变换可以得到的图象.
18.已知函数f(x)=sinxcosx﹣cos2x.
(1)求f(x)的最小正周期;
(2)求f(x)在区间上的最小值,并求取得最小值时x的值.
19.已知函数.
(I)求函数的最小值;
(II)若,求的值.
20.已知向量=(cosα,sinα),=(cosβ,sinβ),|﹣|=.
(1)求cos(α﹣β)的值;
(2)若0<α<,﹣<β<0,且sinβ=﹣,求sinα.
参考答案及解析
1.A
【解析】
5.B
【解析】在中,,
则,得,即,
则.
6.A
【解析】=,
所以,又,函数为奇函数.
7.B
【解析】由已知,
.故选B.
8.B
【解析】由于,,且为锐角,,
,由两边平方得①,
由两边平方得②,由①②得
,
,由于,,11..
【解析】由,,,,,,,
,代入原式得.
12.,.
【解析】
,.
15.(1);(2).
【解析】(1)根据诱导公式及同角三角函数关系式将其化简.(2)根据、为锐角,且,可知,也为锐角.根据同角三角函数关系式可求得的值.由两角和差公式可求得.
(1)
(2)利用同角三角函数关系解方程组,注意α范围,在开方时取负值:,因此代入可求的值
∵,∴,∴或,又α是第三象限角,
(1).
(2)∵且α是第三象限角,∴,∴
17.(Ⅰ)周期,最大值为2;(Ⅱ)见解析.
【解析】(Ⅰ)把函数化为形式,得,由公式得周期,最大值是;(Ⅱ)可考虑怎样由的图象变换到的图象,然后反过来即得:把的图象上各点纵坐标缩短到原来的2倍(横坐标不变),再把所得图象上所有点向左平移个单位,再把所得图象上所有的点的横坐标缩短到原来的2倍(纵坐标18.(1)T=π;(2)时,取得最小值﹣1.21世纪教育网版权所有
【解析】(1)化简函数f(x)为Asin(ωx+φ)+b的形式,求出最小正周期;
(2)由x∈求出2x﹣的取值范围,再计算f(x)的取值范围以及取最小值时x的值.
(1)函数f(x)=sinxcosx﹣cos2x
=sin2x﹣
=(sin2x﹣cos2x)﹣
=sin(2x﹣)﹣,
由得,最小正周期T=π;
(2)∵,∴,
∴,
(II)由(I)得所以,所以(舍)或
又
20.(1);(2).
【解析】(1)=1,同理=1.利用数量积运算性质|﹣|=,可得=,展开即可得出;
(2)由0<α<,﹣<β<0,且sinβ=﹣,可得0<α﹣β<π,,==.
一、选择题
1.化简的结果是( )
A.1 B. C.2 D.
2.化简( )
A. B. C. D.
3.已知,,则是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
4.(α+β)=,tan=,那么tan等于( )
A. B. C. D.
5.在中,,则( )
A. B. C.2 D.
6.函数是( )
A.最小正周期为的奇函数 B.最小正周期为的奇函数
C.最小正周期为的偶函数 D.最小正周期为的偶函数
7.已知角的顶点与原点重合,始边与轴的正半轴重合,终边在直线上,则( )
A. B. C. D.
8.已知,,且为锐角,则( )
A. B.- C.± D.±
9.已知α是三角形的内角,且sinαcosα =,则cosα+sinα的值等于( )
A.± B.± C. D.-
10.在中,已知,,则的值为( )
A. B. C. D.或
二、填空题
11.求值 .
12.已知,则 , .
13.,且,则角的取值范围是 .
14.已知:,,且,则=___ ___ .
三、解答题
15.(1)化简:.
(2)若、为锐角,且,,求的值.
16.已知tanα是关于x的方程的一个实根,且α是第三象限角.
(1)求的值;
(2)求的值.
17.已知函数
(Ⅰ)求该函数的周期和最大值;
(Ⅱ)该函数的图象经过怎样的平移和伸缩变换可以得到的图象.
18.已知函数f(x)=sinxcosx﹣cos2x.
(1)求f(x)的最小正周期;
(2)求f(x)在区间上的最小值,并求取得最小值时x的值.
19.已知函数.
(I)求函数的最小值;
(II)若,求的值.
20.已知向量=(cosα,sinα),=(cosβ,sinβ),|﹣|=.
(1)求cos(α﹣β)的值;
(2)若0<α<,﹣<β<0,且sinβ=﹣,求sinα.
参考答案及解析
1.A
【解析】
5.B
【解析】在中,,
则,得,即,
则.
6.A
【解析】=,
所以,又,函数为奇函数.
7.B
【解析】由已知,
.故选B.
8.B
【解析】由于,,且为锐角,,
,由两边平方得①,
由两边平方得②,由①②得
,
,由于,,11..
【解析】由,,,,,,,
,代入原式得.
12.,.
【解析】
,.
15.(1);(2).
【解析】(1)根据诱导公式及同角三角函数关系式将其化简.(2)根据、为锐角,且,可知,也为锐角.根据同角三角函数关系式可求得的值.由两角和差公式可求得.
(1)
(2)利用同角三角函数关系解方程组,注意α范围,在开方时取负值:,因此代入可求的值
∵,∴,∴或,又α是第三象限角,
(1).
(2)∵且α是第三象限角,∴,∴
17.(Ⅰ)周期,最大值为2;(Ⅱ)见解析.
【解析】(Ⅰ)把函数化为形式,得,由公式得周期,最大值是;(Ⅱ)可考虑怎样由的图象变换到的图象,然后反过来即得:把的图象上各点纵坐标缩短到原来的2倍(横坐标不变),再把所得图象上所有点向左平移个单位,再把所得图象上所有的点的横坐标缩短到原来的2倍(纵坐标18.(1)T=π;(2)时,取得最小值﹣1.21世纪教育网版权所有
【解析】(1)化简函数f(x)为Asin(ωx+φ)+b的形式,求出最小正周期;
(2)由x∈求出2x﹣的取值范围,再计算f(x)的取值范围以及取最小值时x的值.
(1)函数f(x)=sinxcosx﹣cos2x
=sin2x﹣
=(sin2x﹣cos2x)﹣
=sin(2x﹣)﹣,
由得,最小正周期T=π;
(2)∵,∴,
∴,
(II)由(I)得所以,所以(舍)或
又
20.(1);(2).
【解析】(1)=1,同理=1.利用数量积运算性质|﹣|=,可得=,展开即可得出;
(2)由0<α<,﹣<β<0,且sinβ=﹣,可得0<α﹣β<π,,==.
