第三章 三角恒等变换单元综合检测题三(带解析)
文档属性
| 名称 | 第三章 三角恒等变换单元综合检测题三(带解析) |  | |
| 格式 | zip | ||
| 文件大小 | 819.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-08 09:03:57 | ||
图片预览


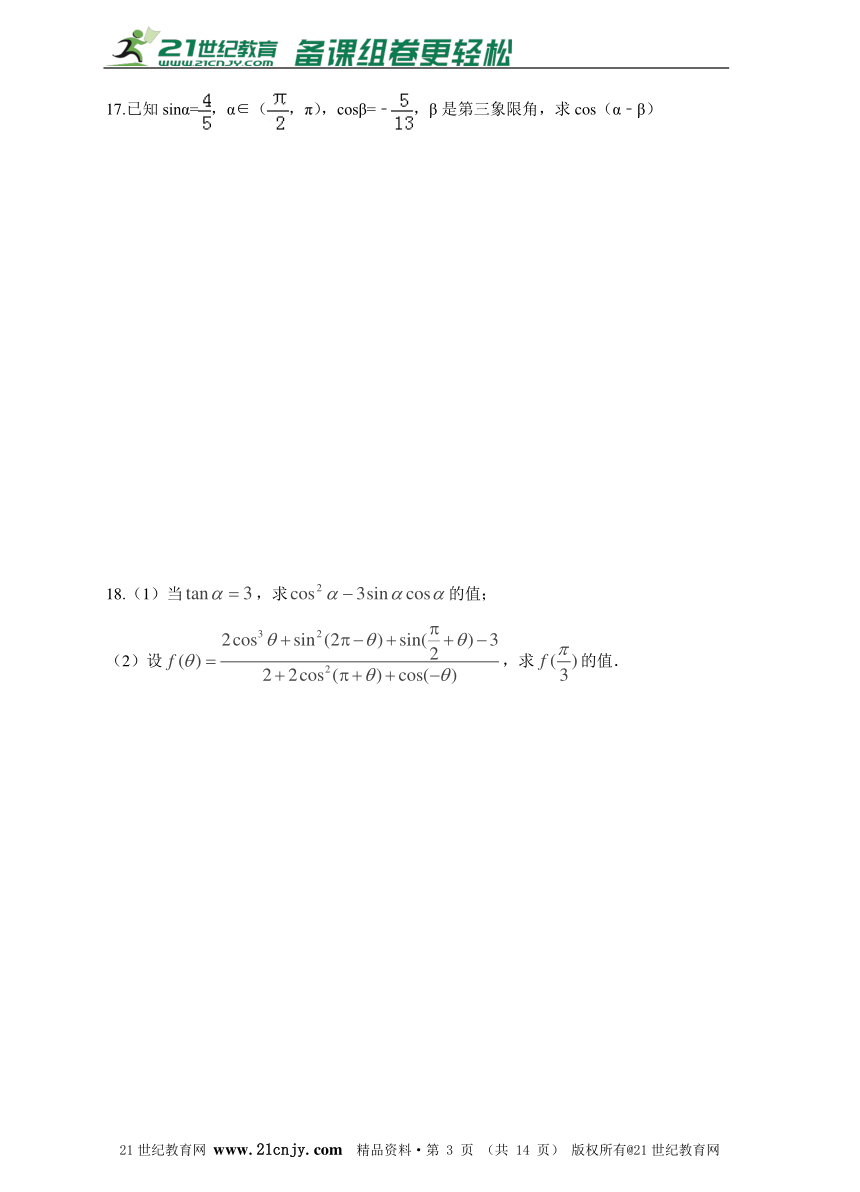


文档简介
第三章 三角恒等变换单元综合检测题三(带解析)
一、选择题
1.计算cos18°cos42°-cos72°cos48°=( )、
A. B. C. D.
2.若2sinx=1+cosx,则的值等于( )
A. B.或不存在 C.2 D.2或
3.设a=cos6°-,b=,则有( )
A.a<b<c B.a<c<b C.a>b>c D.a>c>b
4.已知x∈(-,0),cosx=,则tan2x等于( )
A. B.- C. D.-
5.设函数f(x)=3sinx+2cosx+1.若实数a,b,c使得af(x)+bf(x-c)=1对任意实数x恒成立,则的值为( )www.21-cn-jy.com
A.-1 B. C.1 D.
6.已知△ABC中,a、b、c分别为角A、B、C所在的对边,且a=4,b+c=5,tanB+tanC+=tanB?tanC,则△ABC的面积为( )www-2-1-cnjy-com
A. B.3 C. D.
7.已知正方形ABCD的边长为2,P、Q分别为边AB、DA上的点.设∠BCP=α,∠DCQ=β,若△APQ的周长为4,则α+β=( )2-1-c-n-j-y
A.15° B.30° C.45° D.60°
8.函数的单调递增区间是( )
A.(2kπ-π,2kπ-)(k∈Z) B.(2kπ-,2kπ+)(k∈Z) C.(2kπ-,2k)(k∈Z) D.(kπ-,k)(k∈Z)
9.若0≤θ<2π且满足不等式,那么角θ的取值范围是( )
A. B. C. D.
10.已知,则sinβ=( )
A. B. C. D.
11.在北京召开的第24届国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若直角三角形中较小的锐角记作θ,大正方形的面积是1,小正方形的面积是,则sin2θ-cos2θ的值等于( ) 21*cnjy*com
A.1 B. C. D.-
二、填空题
12.已知,则tanα的值为??? .
13.已知tanx=2,则的值为??? .
14.已知,且,则β-α=??? .
15.△ABC的内角A,B,C所对的边分别为a,b,c,且acosB-bcosA=c,则tan(A-B)的最大值是??? .21·世纪*教育网
三、解答题
16.已知为第二象限角,且,求的值.
17.已知sinα=,α∈(,π),cosβ=﹣,β是第三象限角,求cos(α﹣β)
18.(1)当,求的值;
(2)设,求的值.
19.已知函数,.
(1)求函数的最小正周期;
(2)求函数在区间上的值域.
20.已知函数f(x)=Asin(3x+φ)(A>0.x∈(﹣∞,+∞),0<φ<π)在x=时取得最大值4..21世纪教育网版权所有
(1)求f(x)的最小正周期;
(2)求f(x)的解析式;
(3)若f(α+)=.求tan2α的值.
21.如图,在半径为、圆心角为60°的扇形的弧上任取一点,作扇形的内接矩形,使点在上,点在上,设矩形的面积为.
(1)按下列要求写出函数关系式:
①设,将表示成的函数关系式;
②设,将表示成的函数关系式.
(2)请你选用(1)中的一个函数关系式,求的最大值.
参考答案及解析
1.B 【解析】原式=. 故选B. 2.B 【解析】∵2sinx=1+cosx, ∴2×2sincos=1+(2cos2-1), 21教育网
4.D 【解析】∵cosx=,x∈(-,0), ∴sinx=-.∴tanx=-. ∴tan2x===-×=-. 5.A 【解析】由题设可得f(x)=sin(x+θ)+1,f(x-c)=sin(x+θ-c)+1,其中cosθ=,sinθ=(0<θ<), ∴af(x)+bf(x-c)=1可化成asin(x+θ)+bsin(x+θ-c)+a+b=1, 即(a+bcosc)sin(x+θ)-bsinccos(x+θ)+(a+b-1)=0, 由已知条件,上式对任意x∈R恒成立,故必有, 若b=0,则式(1)与式(3)矛盾; 故此b≠0,由(2)式得到:sinc=0, 当cosc=1时,有矛盾,故cosc=-1, 由①③知a=b=, 则=-1. 6.C 【解析】由题意可得 tanB+tanC=(-1+tanB?tanC),∴tan(B+C)==-, ∴B+C=,∴A=. 21cnjy.com
∴△CDQ≌△CBE(SAS), ∴∠BCE=∠DCQ=β, 在Rt△CDQ中,设|DQ|=|BE|=x,|CD|=2, 可得x=2tanβ,AQ=2-2tanβ, 在Rt△CPB中,设|PB|=y,|CB|=2, 可得y=2tanα,|AP|=2-2tanα, 又△APQ的周长为4, ∴|PQ|=4-(|AQ|+|AP|)=4-(2-2tanβ+2-2tanα)=2(tanα+tanβ),即tanα+tanβ=|PQ|, 在Rt△APQ中,根据勾股定理得:|PQ|=(2-2tanβ)2+(2-2tanα)2, 整理得:tanαtanβ=1-|PQ|,
变形得:<, 解得:cosθ<0,又0≤θ<2π, 则角θ的取值范围是. 10.B 【解析】∵,∴α+β为钝角,∴cos(α+β)=-,cosα=. ∴sinβ=sin[( α+β)-α]=sin( α+β)cosα-cos( α+β)sinα=-(-)=. 11.D 【解析】设三角形短直角边为x ∵S小正方形= ∴小正方形边长= ∴直角三角形另一条直角边为x+
则= = = = 14. 【解析】∵0<α<,tanα=, ∴cosα==,sinα==, ∵π<β<,cosβ=-, 即tanA=4tanB; ∵tan(A-B)===≤=, ∴tan(A-B)的最大值为, 16.2·1·c·n·j·y
【解析】先对,可得,
根据为第二象限角,且,可计算出,
然后代入代数式计算即可.
因为,
又当为第二象限角,且时,
18.;(2).
【解析】(1)利用同角三角函数的基本关系,将原式转化为关于的表达式,从而求解;(2)利用诱导公式将化简为关于的函数关系式,从而求解.【来源:21·世纪·教育·网】
(1)∵,且,
∴原式;(2)
(1)由条件可得,
所以该函数的最小正周期
(2),,
当时,函数取得最大值为,当时,函数取得最小值为1
函数的值域为
20.(1);(2)f(x)=4sin(3x+);(3)±.
【解析】(1)根据题意,求出f(x)的最小正周期T=;
(2)根据f(x)max=f()求出A与φ的值即可;
(3)根据f(α+)的值求出cos2α与sin2α的值,再求出tan2α的值.
(1)∵函数f(x)=Asin(3x+φ),
∴f(x)的最小正周期为T==;
(2)∵f(x)max=f()=Asin(3×+φ)=4,
∴A=4,且sin(+φ)=1,
又∵0<φ<π,
21.(1) ①(),②();(2) 选②,当时,y取得最大值为.
【解析】(1) ①设,则,三角形中有,又,则,又,可得表达式, ②当时,,三角形中同样有,,,由得表达式;21·cn·jy·com
(2) 将化为,可得最大值.
(1) ① 因为,所以,又,
(2)由②得=
故当时,y取得最大值为
一、选择题
1.计算cos18°cos42°-cos72°cos48°=( )、
A. B. C. D.
2.若2sinx=1+cosx,则的值等于( )
A. B.或不存在 C.2 D.2或
3.设a=cos6°-,b=,则有( )
A.a<b<c B.a<c<b C.a>b>c D.a>c>b
4.已知x∈(-,0),cosx=,则tan2x等于( )
A. B.- C. D.-
5.设函数f(x)=3sinx+2cosx+1.若实数a,b,c使得af(x)+bf(x-c)=1对任意实数x恒成立,则的值为( )www.21-cn-jy.com
A.-1 B. C.1 D.
6.已知△ABC中,a、b、c分别为角A、B、C所在的对边,且a=4,b+c=5,tanB+tanC+=tanB?tanC,则△ABC的面积为( )www-2-1-cnjy-com
A. B.3 C. D.
7.已知正方形ABCD的边长为2,P、Q分别为边AB、DA上的点.设∠BCP=α,∠DCQ=β,若△APQ的周长为4,则α+β=( )2-1-c-n-j-y
A.15° B.30° C.45° D.60°
8.函数的单调递增区间是( )
A.(2kπ-π,2kπ-)(k∈Z) B.(2kπ-,2kπ+)(k∈Z) C.(2kπ-,2k)(k∈Z) D.(kπ-,k)(k∈Z)
9.若0≤θ<2π且满足不等式,那么角θ的取值范围是( )
A. B. C. D.
10.已知,则sinβ=( )
A. B. C. D.
11.在北京召开的第24届国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若直角三角形中较小的锐角记作θ,大正方形的面积是1,小正方形的面积是,则sin2θ-cos2θ的值等于( ) 21*cnjy*com
A.1 B. C. D.-
二、填空题
12.已知,则tanα的值为??? .
13.已知tanx=2,则的值为??? .
14.已知,且,则β-α=??? .
15.△ABC的内角A,B,C所对的边分别为a,b,c,且acosB-bcosA=c,则tan(A-B)的最大值是??? .21·世纪*教育网
三、解答题
16.已知为第二象限角,且,求的值.
17.已知sinα=,α∈(,π),cosβ=﹣,β是第三象限角,求cos(α﹣β)
18.(1)当,求的值;
(2)设,求的值.
19.已知函数,.
(1)求函数的最小正周期;
(2)求函数在区间上的值域.
20.已知函数f(x)=Asin(3x+φ)(A>0.x∈(﹣∞,+∞),0<φ<π)在x=时取得最大值4..21世纪教育网版权所有
(1)求f(x)的最小正周期;
(2)求f(x)的解析式;
(3)若f(α+)=.求tan2α的值.
21.如图,在半径为、圆心角为60°的扇形的弧上任取一点,作扇形的内接矩形,使点在上,点在上,设矩形的面积为.
(1)按下列要求写出函数关系式:
①设,将表示成的函数关系式;
②设,将表示成的函数关系式.
(2)请你选用(1)中的一个函数关系式,求的最大值.
参考答案及解析
1.B 【解析】原式=. 故选B. 2.B 【解析】∵2sinx=1+cosx, ∴2×2sincos=1+(2cos2-1), 21教育网
4.D 【解析】∵cosx=,x∈(-,0), ∴sinx=-.∴tanx=-. ∴tan2x===-×=-. 5.A 【解析】由题设可得f(x)=sin(x+θ)+1,f(x-c)=sin(x+θ-c)+1,其中cosθ=,sinθ=(0<θ<), ∴af(x)+bf(x-c)=1可化成asin(x+θ)+bsin(x+θ-c)+a+b=1, 即(a+bcosc)sin(x+θ)-bsinccos(x+θ)+(a+b-1)=0, 由已知条件,上式对任意x∈R恒成立,故必有, 若b=0,则式(1)与式(3)矛盾; 故此b≠0,由(2)式得到:sinc=0, 当cosc=1时,有矛盾,故cosc=-1, 由①③知a=b=, 则=-1. 6.C 【解析】由题意可得 tanB+tanC=(-1+tanB?tanC),∴tan(B+C)==-, ∴B+C=,∴A=. 21cnjy.com
∴△CDQ≌△CBE(SAS), ∴∠BCE=∠DCQ=β, 在Rt△CDQ中,设|DQ|=|BE|=x,|CD|=2, 可得x=2tanβ,AQ=2-2tanβ, 在Rt△CPB中,设|PB|=y,|CB|=2, 可得y=2tanα,|AP|=2-2tanα, 又△APQ的周长为4, ∴|PQ|=4-(|AQ|+|AP|)=4-(2-2tanβ+2-2tanα)=2(tanα+tanβ),即tanα+tanβ=|PQ|, 在Rt△APQ中,根据勾股定理得:|PQ|=(2-2tanβ)2+(2-2tanα)2, 整理得:tanαtanβ=1-|PQ|,
变形得:<, 解得:cosθ<0,又0≤θ<2π, 则角θ的取值范围是. 10.B 【解析】∵,∴α+β为钝角,∴cos(α+β)=-,cosα=. ∴sinβ=sin[( α+β)-α]=sin( α+β)cosα-cos( α+β)sinα=-(-)=. 11.D 【解析】设三角形短直角边为x ∵S小正方形= ∴小正方形边长= ∴直角三角形另一条直角边为x+
则= = = = 14. 【解析】∵0<α<,tanα=, ∴cosα==,sinα==, ∵π<β<,cosβ=-, 即tanA=4tanB; ∵tan(A-B)===≤=, ∴tan(A-B)的最大值为, 16.2·1·c·n·j·y
【解析】先对,可得,
根据为第二象限角,且,可计算出,
然后代入代数式计算即可.
因为,
又当为第二象限角,且时,
18.;(2).
【解析】(1)利用同角三角函数的基本关系,将原式转化为关于的表达式,从而求解;(2)利用诱导公式将化简为关于的函数关系式,从而求解.【来源:21·世纪·教育·网】
(1)∵,且,
∴原式;(2)
(1)由条件可得,
所以该函数的最小正周期
(2),,
当时,函数取得最大值为,当时,函数取得最小值为1
函数的值域为
20.(1);(2)f(x)=4sin(3x+);(3)±.
【解析】(1)根据题意,求出f(x)的最小正周期T=;
(2)根据f(x)max=f()求出A与φ的值即可;
(3)根据f(α+)的值求出cos2α与sin2α的值,再求出tan2α的值.
(1)∵函数f(x)=Asin(3x+φ),
∴f(x)的最小正周期为T==;
(2)∵f(x)max=f()=Asin(3×+φ)=4,
∴A=4,且sin(+φ)=1,
又∵0<φ<π,
21.(1) ①(),②();(2) 选②,当时,y取得最大值为.
【解析】(1) ①设,则,三角形中有,又,则,又,可得表达式, ②当时,,三角形中同样有,,,由得表达式;21·cn·jy·com
(2) 将化为,可得最大值.
(1) ① 因为,所以,又,
(2)由②得=
故当时,y取得最大值为
