12.5-2十字相乘法分解因式 课件
文档属性
| 名称 | 12.5-2十字相乘法分解因式 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 295.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-08 15:53:40 | ||
图片预览



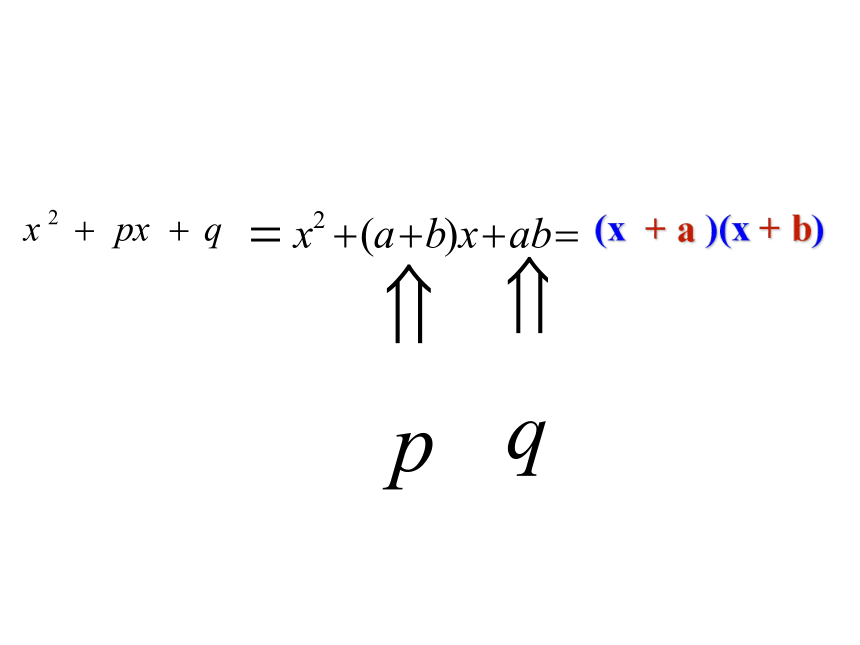



文档简介
课件15张PPT。十字相乘法1、口答计算结果看你行不行(x+3)(x+4)
(x+3)(x-4)
(3) (x-3)(x+4)
(4) (x-3)(x-4)2、提问:你有什么快速计算类似以上多项式的方法吗?
整式乘法中,有
(x+a)(x+b)=x2+(a+b)x+ab
(x+a)(x+b)=x2+(a+b)x+ab观察与发现两个一次二项式相乘的积一个二次三项式整式的乘法反过来,得x2+(a+b)x+ab=(x+a)(x+b)一个二次三项式两个一次二项式相乘的积因式分解 如果二次三项式x2+px+q中的常数项系数q能分解成两个因数a、b的积,而且一次项系数p又恰好是a+b,那么x2+px+q就可以进行如上的因式分解。(x + a )(x + b)例一:或步骤:①竖分二次项与常数项②交叉相乘,和相加③检验确定,横写因式十字相乘法(借助十字交叉线分解因式的方法)
顺口溜:竖分常数交叉验,
横写因式不能乱。试一试:小结:用十字相乘法把形如二次三项式分解因式使
(顺口溜:竖分常数交叉验,横写因式不能乱。)
练一练:小结:用十字相乘法把形如二次三项式分解因式
当q>0时,q分解的因数a、b( )
当q<0时, q分解的因数a、b( )同号异号将下列各式分解因式观察:p与a、b符号关系
小结:且(a、b符号)与p符号相同(其中绝对值较大的因数符号)与p符号相同练习:在 横线上 填 、 符号
=(x 3)(x 1) =(x 3)(x 1)=(y 4)(y 5)=(t 4)(t 14)++-+---+当q>0时,q分解的因数a、b( 同号 )且(a、b符号)与p符号相同当q<0时, q分解的因数a、b( 异号) (其中绝对值较大的因数符号)与p符号相同 五、选择题:
以下多项式中分解因式为 的多项式是( )
A
B
C
D
c 试将分解因式
提示:当二次项系数为-1时 ,先提出负号再因式分解 。 六、独立练习:把下列各式分解因式
? 思考题:1、含有x的二次三项式,其中x2系数是1,常数项为12,并能分解因式,这样的多项式共有几个?若一次项的系数为整数,则有6个;否则有无数个!!2、分解因式
(1).x2+(a-1)x-a;
(2).(x+y) 2+8(x+y)-48;
(1)(x+a)(x-1)
(2)(x+y+12)(x+y-4)小结通过这节课的学习你有什么收获? 1.十字相乘法分解因式的公式:x2+(a+b)x+ab=(x+a)(x+b)3.在用十字相乘法分解因式时,因为常数项的分解因数有多种情况,所以通常要经过多次的尝试才能确定采用哪组分解来进行分解因式。2.能用十字相乘法来分解因式的二次三项式的系数的特点:常数项能分解成两个数的积,且这两个数的和恰好等于一次项的系数。1、十字相乘法(借助十字交叉线分解因式的方法)2、用十字相乘法把形如x2 + px +q 二次三项式分解因式 3、 x2+px+q=(x+a)(x+b) 其中q、p、a、b之间的符号关系q>0时,q分解的因数a、b( 同号 )且(a、b符号)与p符号相同 当q<0时, q分解的因数a、b( 异号) (其中绝对值较大的因数符号)
与p符号相同本节总结
(x+3)(x-4)
(3) (x-3)(x+4)
(4) (x-3)(x-4)2、提问:你有什么快速计算类似以上多项式的方法吗?
整式乘法中,有
(x+a)(x+b)=x2+(a+b)x+ab
(x+a)(x+b)=x2+(a+b)x+ab观察与发现两个一次二项式相乘的积一个二次三项式整式的乘法反过来,得x2+(a+b)x+ab=(x+a)(x+b)一个二次三项式两个一次二项式相乘的积因式分解 如果二次三项式x2+px+q中的常数项系数q能分解成两个因数a、b的积,而且一次项系数p又恰好是a+b,那么x2+px+q就可以进行如上的因式分解。(x + a )(x + b)例一:或步骤:①竖分二次项与常数项②交叉相乘,和相加③检验确定,横写因式十字相乘法(借助十字交叉线分解因式的方法)
顺口溜:竖分常数交叉验,
横写因式不能乱。试一试:小结:用十字相乘法把形如二次三项式分解因式使
(顺口溜:竖分常数交叉验,横写因式不能乱。)
练一练:小结:用十字相乘法把形如二次三项式分解因式
当q>0时,q分解的因数a、b( )
当q<0时, q分解的因数a、b( )同号异号将下列各式分解因式观察:p与a、b符号关系
小结:且(a、b符号)与p符号相同(其中绝对值较大的因数符号)与p符号相同练习:在 横线上 填 、 符号
=(x 3)(x 1) =(x 3)(x 1)=(y 4)(y 5)=(t 4)(t 14)++-+---+当q>0时,q分解的因数a、b( 同号 )且(a、b符号)与p符号相同当q<0时, q分解的因数a、b( 异号) (其中绝对值较大的因数符号)与p符号相同 五、选择题:
以下多项式中分解因式为 的多项式是( )
A
B
C
D
c 试将分解因式
提示:当二次项系数为-1时 ,先提出负号再因式分解 。 六、独立练习:把下列各式分解因式
? 思考题:1、含有x的二次三项式,其中x2系数是1,常数项为12,并能分解因式,这样的多项式共有几个?若一次项的系数为整数,则有6个;否则有无数个!!2、分解因式
(1).x2+(a-1)x-a;
(2).(x+y) 2+8(x+y)-48;
(1)(x+a)(x-1)
(2)(x+y+12)(x+y-4)小结通过这节课的学习你有什么收获? 1.十字相乘法分解因式的公式:x2+(a+b)x+ab=(x+a)(x+b)3.在用十字相乘法分解因式时,因为常数项的分解因数有多种情况,所以通常要经过多次的尝试才能确定采用哪组分解来进行分解因式。2.能用十字相乘法来分解因式的二次三项式的系数的特点:常数项能分解成两个数的积,且这两个数的和恰好等于一次项的系数。1、十字相乘法(借助十字交叉线分解因式的方法)2、用十字相乘法把形如x2 + px +q 二次三项式分解因式 3、 x2+px+q=(x+a)(x+b) 其中q、p、a、b之间的符号关系q>0时,q分解的因数a、b( 同号 )且(a、b符号)与p符号相同 当q<0时, q分解的因数a、b( 异号) (其中绝对值较大的因数符号)
与p符号相同本节总结
