福建省泉州市泉港区三川中学华师大版八年级数学上册课件11.1-1平方根与立方根(2课时)
文档属性
| 名称 | 福建省泉州市泉港区三川中学华师大版八年级数学上册课件11.1-1平方根与立方根(2课时) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-08 18:46:15 | ||
图片预览







文档简介
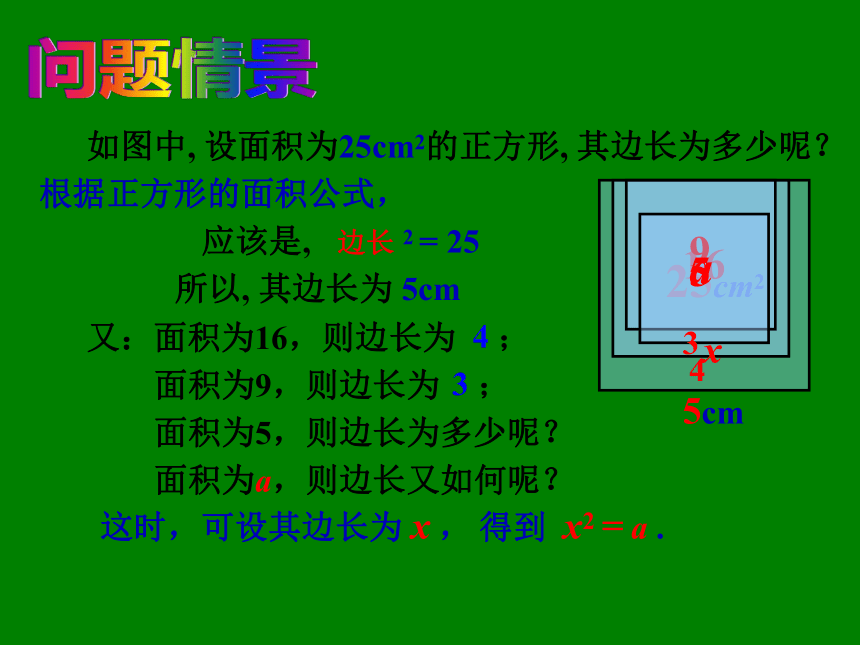
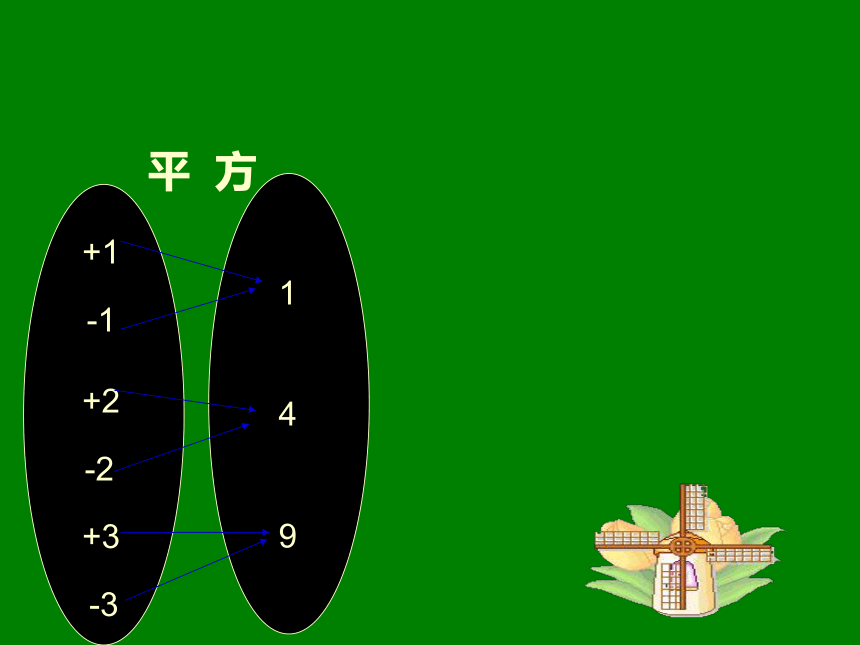
课件30张PPT。鼓士气 创佳绩 简分析;新要求。11.1《平方根 》如图中, 设面积为25cm2的正方形, 其边长为多少呢? 5cm问题情景x应该是, 2 = 25 又:面积为16,则边长为 4 ; a5边长所以, 其边长为 5cm 4 面积为9,则边长为 3 ; 3 面积为5,则边长为多少呢? 面积为a,则边长又如何呢? 根据正方形的面积公式, 这时,可设其边长为 x , 得到 x2 = a . 新知概念如果一个数 x 的平方等于 a, 那么这个数 x 叫做 a 的平方根. 就是说, 当 x2 =a 时, 称 x 是 a 的平方根. (a≥0)根据平方根的意义,我们可以利用平方运算来求一个数的平方根。+1-1+2-2+3-3149平 方x2 X1
4
9
+1
-1
+2
-2
+3
-3
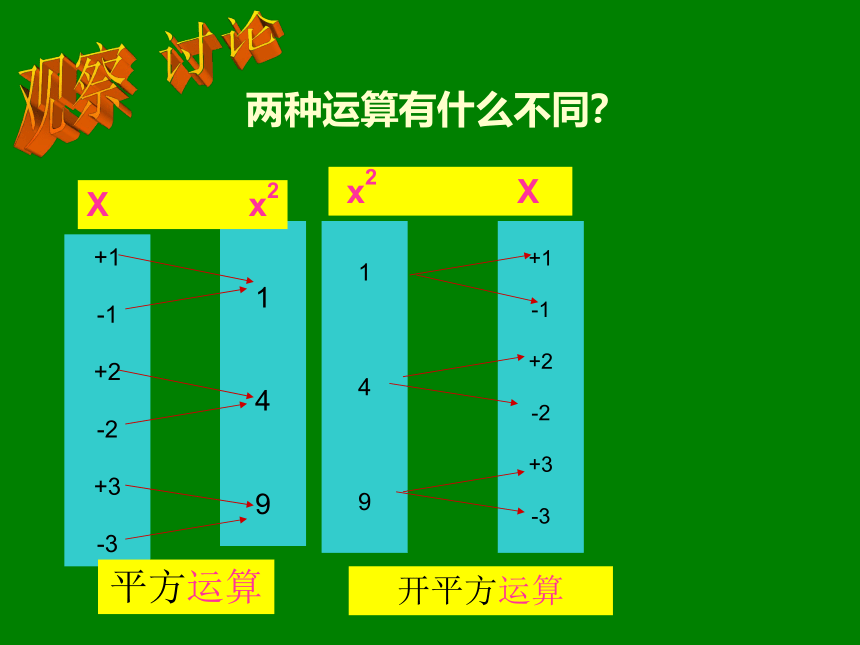
两种运算有什么不同?
+1
-1
+2
-2
+3
-3
1
4
9X x21
4
9
+1
-1
+2
-2
+3
-3
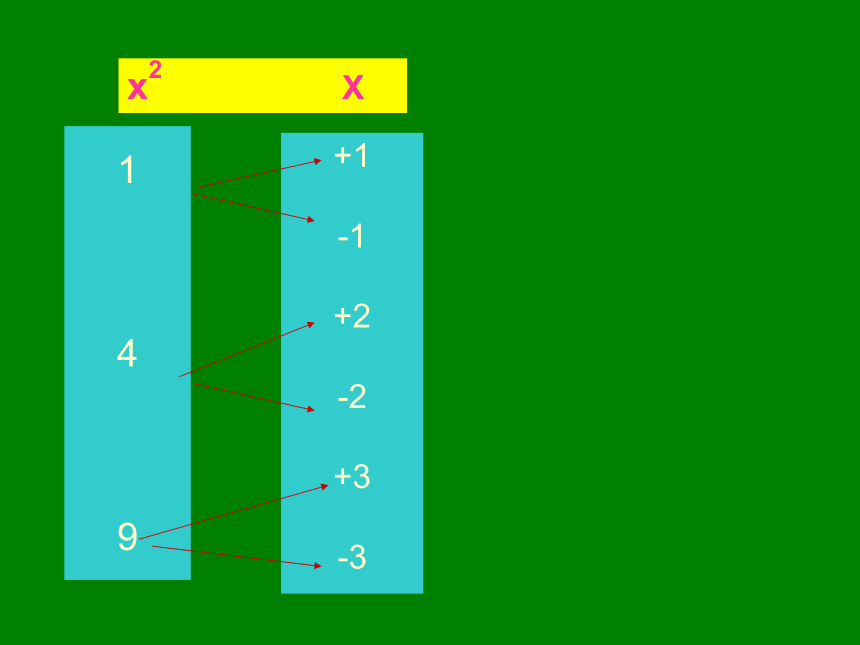
平方运算 x2 X观察 讨论开平方运算a的平方根表示为a的平方根是如:6的平方根表示成± ± 求一个数a的平方根的运算,叫做开平方. 平方与开平方互为逆运算.练一练 口算下列各数的平方根(1)64 (3)0.04(4) 0 X2 1 16 36 0.49 4/25
X ±1 ±4 ±6 ±0.7 ±2/5 观察性质:正数有两个平方根,它们互为相反数. 0有一个平方根,它是0本身.负数没有平方根.议一议性质:正数有两个平方根,它们互为相反数. ( )2=0 ( )2= - 4 性质 正数有两个平方根,
它们互为相反数.
0有一个平方根,它是0本身.
负数没有平方根.为了趣味接力比赛,要在运动场上圈出一个面积为100平方米的正方形场地,这个正方形场地的边长为多少? ?-10米x2 = a正数a的正的平方根又叫做a的算术平方根.例 1 把下列各数开平方 1) 100 2)解:1) 因为 (±10 )2 =100, 所以100的平方根是 ±10, 例题教学3) 0.25
注:第2)、3)题的解答过程让学生说。例2 求下列各式的值:(3)解:(1)注:第(2)、(3)题的解答过程让学生说。 达标训练:
(1)49的平方根是( ),算术平方根是( );
(2)0.09的平方根是( ),算术平方根是( );
(3)若- 是x的一个平方根,那么x的另一个平方根是( );
(4)平方根等于它本身的数是( ),算术平方根等于
它本身的数是( );
(5) 一个数的平方等于 0.01 ,这个数是( );
±7±0.3±0.170,100.3辨一辨 下列叙述正确的打“ √” ,错误的打“×”:⑴ 16的平方根是 ±4; ( ) √⑵ ±7是49的平方根 ; ( ) √⑶ 112的平方根是11; ( ) ×⑷ -9是81的平方根; ( ) √⑸ 52的平方根是±25; ( ) ×⑹ -9的平方根是 -3; ( ) ×(7) 只有一个平方根的数是0; ( ) √
学校要举行美术作品比赛,小明很高兴,他想裁出一块面积为50平方厘米 的正方形画布,画上自己的得意之作参比赛,这块正方形画布的边长应取多少厘米 ?
试一试思维拓展求下列各式中的x: 1. x2=16 2. 64x2=25 3. (x-1)2=9 x=±4 x=± x-1=±3 x=4 或x= -2 请记住:12=1
22=4
32=9
42=16
52=25
62=36
72=49
82=64
92=81
102=100112=121
122=144
132=169
142=196
152=225
162=256
172=289
182=324
192=361
202=400252=625
352=1225
452=2025
552=3025
652=4225
752=5625
852=7225
952=9025
本节课你有哪些收获?
平方根的概念(二次方根)
平方根的性质
3 开平方运算
4 正数a的平方根可以用符号“± ”表示,
读作“正.负根号a”
强调: 符号“± ” 只有a≥0时有意义,
a<0时无意义.(第2课时)填一填 1. 平方根恰是本身的数是_____; 算术平方根恰是本 身的数是______. 0 0 、1 2. 4的平方是_____; 4的平方根是_____. 16 ±2 3 ±2 5 -6 ±7 5. 81的算术平方根是____; (-9)2的平方根是____.9 81 ±9 ±3 ±9 3 9 典例讲解解: (1) x2=2.25 (2) x-1=±2 (3) x=49 (4) x-1=9
∴x=10∴x=±1.5 ∴x=3或x=-1 你能求出下列各式中的未知数x吗?计算器的使用例3、用计算器求下列各数的算术平方根: (1)529;(2)1225;(3)44.81;例:(1)利用计算器键入: “ ”、 “5” 、“2”、“9”、“=”注:第(2)、(3)题的解答过程让学生说。操作: ≈7.071 ≈6.557 = 9= 0≈11.09 ≈31.62 ≈2.646 试一试 比较: < < < < < < 0 < 7 < 43 < 50 < 81 < 123 < 1000 x 的值随着x的增大而增大。 结论: 叙述: 非负数的算术平方根随着被开方数
的增大而增大。 例练估算下列各值在哪两个整数之间: 解:∵1 <2 <4 注: 一般先找出被开方数前后的两个完全平方数, 再进行算术平方根的比较估算. 回顾小结1、算术平方根与平方根:算术平方根是平方根中正的一个值, 平方根一般有互为相反数的两个值.3、进行算术平方根估值时, 先找出被开方数的前后 只有一个值; 算术平方根只表示为: , 而平方根需表示为: ±2、计算器操作算术平方根时, 根据精度要求取小数。 两个完全平方数, 再根据非负数的算术平方根随被开方数的增大而增大进行估算.作业 1.必做题 习题11.1 第1、2题
2.选做题
2a-3和3a-22是m的两个平方根,试求m的值.
别忘了作业 在教学中我们一个不经意的点头肯定,一句赞赏的话语,都可以成为学生学习力量的源泉.所以,我根据特定的评价对象,利用多元的评价目标,多样的评价方法,不断激发学生的学习动机.
教学评价 谢 谢
4
9
+1
-1
+2
-2
+3
-3
两种运算有什么不同?
+1
-1
+2
-2
+3
-3
1
4
9X x21
4
9
+1
-1
+2
-2
+3
-3
平方运算 x2 X观察 讨论开平方运算a的平方根表示为a的平方根是如:6的平方根表示成± ± 求一个数a的平方根的运算,叫做开平方. 平方与开平方互为逆运算.练一练 口算下列各数的平方根(1)64 (3)0.04(4) 0 X2 1 16 36 0.49 4/25
X ±1 ±4 ±6 ±0.7 ±2/5 观察性质:正数有两个平方根,它们互为相反数. 0有一个平方根,它是0本身.负数没有平方根.议一议性质:正数有两个平方根,它们互为相反数. ( )2=0 ( )2= - 4 性质 正数有两个平方根,
它们互为相反数.
0有一个平方根,它是0本身.
负数没有平方根.为了趣味接力比赛,要在运动场上圈出一个面积为100平方米的正方形场地,这个正方形场地的边长为多少? ?-10米x2 = a正数a的正的平方根又叫做a的算术平方根.例 1 把下列各数开平方 1) 100 2)解:1) 因为 (±10 )2 =100, 所以100的平方根是 ±10, 例题教学3) 0.25
注:第2)、3)题的解答过程让学生说。例2 求下列各式的值:(3)解:(1)注:第(2)、(3)题的解答过程让学生说。 达标训练:
(1)49的平方根是( ),算术平方根是( );
(2)0.09的平方根是( ),算术平方根是( );
(3)若- 是x的一个平方根,那么x的另一个平方根是( );
(4)平方根等于它本身的数是( ),算术平方根等于
它本身的数是( );
(5) 一个数的平方等于 0.01 ,这个数是( );
±7±0.3±0.170,100.3辨一辨 下列叙述正确的打“ √” ,错误的打“×”:⑴ 16的平方根是 ±4; ( ) √⑵ ±7是49的平方根 ; ( ) √⑶ 112的平方根是11; ( ) ×⑷ -9是81的平方根; ( ) √⑸ 52的平方根是±25; ( ) ×⑹ -9的平方根是 -3; ( ) ×(7) 只有一个平方根的数是0; ( ) √
学校要举行美术作品比赛,小明很高兴,他想裁出一块面积为50平方厘米 的正方形画布,画上自己的得意之作参比赛,这块正方形画布的边长应取多少厘米 ?
试一试思维拓展求下列各式中的x: 1. x2=16 2. 64x2=25 3. (x-1)2=9 x=±4 x=± x-1=±3 x=4 或x= -2 请记住:12=1
22=4
32=9
42=16
52=25
62=36
72=49
82=64
92=81
102=100112=121
122=144
132=169
142=196
152=225
162=256
172=289
182=324
192=361
202=400252=625
352=1225
452=2025
552=3025
652=4225
752=5625
852=7225
952=9025
本节课你有哪些收获?
平方根的概念(二次方根)
平方根的性质
3 开平方运算
4 正数a的平方根可以用符号“± ”表示,
读作“正.负根号a”
强调: 符号“± ” 只有a≥0时有意义,
a<0时无意义.(第2课时)填一填 1. 平方根恰是本身的数是_____; 算术平方根恰是本 身的数是______. 0 0 、1 2. 4的平方是_____; 4的平方根是_____. 16 ±2 3 ±2 5 -6 ±7 5. 81的算术平方根是____; (-9)2的平方根是____.9 81 ±9 ±3 ±9 3 9 典例讲解解: (1) x2=2.25 (2) x-1=±2 (3) x=49 (4) x-1=9
∴x=10∴x=±1.5 ∴x=3或x=-1 你能求出下列各式中的未知数x吗?计算器的使用例3、用计算器求下列各数的算术平方根: (1)529;(2)1225;(3)44.81;例:(1)利用计算器键入: “ ”、 “5” 、“2”、“9”、“=”注:第(2)、(3)题的解答过程让学生说。操作: ≈7.071 ≈6.557 = 9= 0≈11.09 ≈31.62 ≈2.646 试一试 比较: < < < < < < 0 < 7 < 43 < 50 < 81 < 123 < 1000 x 的值随着x的增大而增大。 结论: 叙述: 非负数的算术平方根随着被开方数
的增大而增大。 例练估算下列各值在哪两个整数之间: 解:∵1 <2 <4 注: 一般先找出被开方数前后的两个完全平方数, 再进行算术平方根的比较估算. 回顾小结1、算术平方根与平方根:算术平方根是平方根中正的一个值, 平方根一般有互为相反数的两个值.3、进行算术平方根估值时, 先找出被开方数的前后 只有一个值; 算术平方根只表示为: , 而平方根需表示为: ±2、计算器操作算术平方根时, 根据精度要求取小数。 两个完全平方数, 再根据非负数的算术平方根随被开方数的增大而增大进行估算.作业 1.必做题 习题11.1 第1、2题
2.选做题
2a-3和3a-22是m的两个平方根,试求m的值.
别忘了作业 在教学中我们一个不经意的点头肯定,一句赞赏的话语,都可以成为学生学习力量的源泉.所以,我根据特定的评价对象,利用多元的评价目标,多样的评价方法,不断激发学生的学习动机.
教学评价 谢 谢
