福建省泉州市泉港区三川中学华师大版八年级数学上册课件12.3-2两数和的平方
文档属性
| 名称 | 福建省泉州市泉港区三川中学华师大版八年级数学上册课件12.3-2两数和的平方 |  | |
| 格式 | zip | ||
| 文件大小 | 556.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-08 19:34:32 | ||
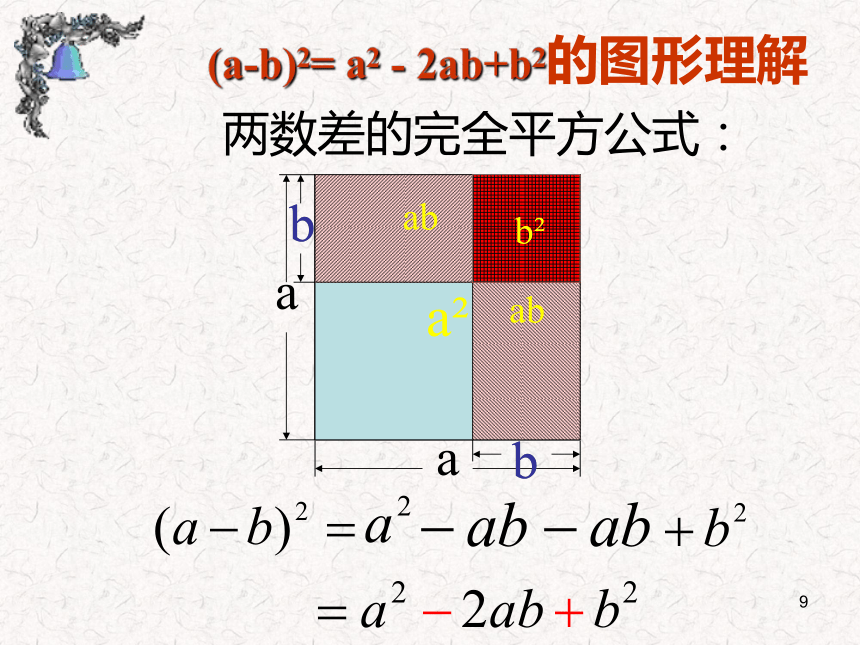
图片预览




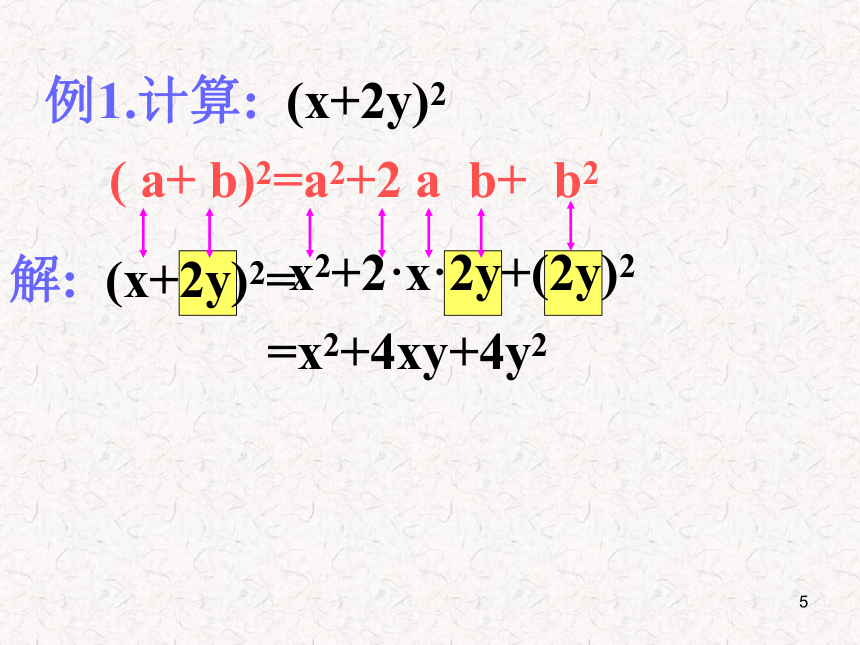



文档简介
课件22张PPT。1计算:(1) ( a+b)+(a-b)(2) (a+b)(a+b)(3) (a+b)(a-b)课前热身:(用幂的形式表示为___________)(a+b)22??12.3乘法公式
(两数和的平方)3ab这是一块田地的总面积,试比较你发现了什么?ba说一说4 (a+b)2=a2+2ab+b2你能用自己的话叙述一下上面的公式吗?两数和的完全平方公式左边是两项的和的平方,即(首+尾)2右边是三项,第一项是首的平方,第二项是首尾乘积的2倍,第三项是尾的平方5例1.计算: (x+2y)2解: (x+2y)2=( a+ b)2=a2+2 a b+ b2=x2+4xy+4y2x2+2·x·2y+(2y)26做一做 (a+1 )2 = ( )2 +2( )( )+ ( )2 (-4x+5y)2 =( )2 +2( )( )+ ( )2
=
(2) (2a+3b ) 2 = ( )2 +2( )( )+ ( )2 利用两数和的平方公式计算: ==7提问:(a-b)2等于什么? 是否可以写成[a+(-b)]2? 你能继续做下去吗?(a-b)2= a2 - 2ab+b28 (a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2 完全平方公式首平方,尾平方,首尾两倍中间放 公式变形为
(首±尾)2=首2±2×首×尾+尾29(a-b)2b2两数差的完全平方公式: (a-b)2= a2 - 2ab+b2的图形理解10例2.计算: (x-2y)2(x - 2y )2=(a - b )2 =a2 - 2 a b + b2x2 - 2· x· 2y +( 2y )2 =x2 - 4xy+4y211做一做 (r-h )2 = ( )2 –2( )( )+ ( )2 (-2x-3y)2 =( )2 –2( )( )+ ( )2
=
(2) ( m-2) 2 = ( )2 –2( )( )+ ( )2 利用两数差的平方公式计算: ==12 例3 用完全平方公式计算:(1)(x+2y)2(2)(2a-5)2(3)(-2s+t)2(4)(-3x-4y)2=X2+4xy+4y2=4a2-20a+25=4s2-4st+t2 =9x2+24xy+16y2思考: (1)完全平方展开有几项?
(2)每一项的符号特征?13
(7-y )2 =比较下列计算结果,你能得到什么结论? (2s-t )2=(-2x-3y )2=(a-b)2= (-a+b )2互为相反数的两个数的完全平方相等(2) (-2s+t)2=(1) (y-7)2 = (3) (2x+3y)2=(-a-b)2= (a+b )214 比较平方差公式和完全平方公式:(a-b)(a+b)= a2-b2( a+ b)2=a2+2 a b+ b2( a- b)2= a2-2 a b+ b2 平方差公式和完全平方公式都叫乘法公式15练一练选择适当的公式计算:
(1)(2x-1)(-1+2x); (2) (-2x-y)(2x-y)
(3) (-a+5)(-a-5); (4) (ab-1)(-ab+1)16 完全平方公式口诀:首平方,尾平方,首尾两倍中间放 我们把两数和的平方公式与两数差的平方公式统称为完全平方公式。(也叫乘法公式)小结在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2;17发散练习,勇于创新1.如果x2-6x+N是一个完全平方式,那么N是( )
(A ) 11 (B) 9 (C) -11 (D) -93.已知(a+b)2=11 , ab=1 , 求(a-b)2的值.B2.如果x2-kx+9是一个完全平方式,那么k是( )
(A ) ±3 (B) 6 (C) -6 (D) ±6 D18(a+b)2 = a2+2ab+b2(a-b)2 = a2-2ab+b219提高题1、计算:2、若 ,则
= 。20a2+b2 =(a+b)2 -2ab21想一想22拓展:
1.计算:
2.已知 求下列各式的值
(1). (2).
(两数和的平方)3ab这是一块田地的总面积,试比较你发现了什么?ba说一说4 (a+b)2=a2+2ab+b2你能用自己的话叙述一下上面的公式吗?两数和的完全平方公式左边是两项的和的平方,即(首+尾)2右边是三项,第一项是首的平方,第二项是首尾乘积的2倍,第三项是尾的平方5例1.计算: (x+2y)2解: (x+2y)2=( a+ b)2=a2+2 a b+ b2=x2+4xy+4y2x2+2·x·2y+(2y)26做一做 (a+1 )2 = ( )2 +2( )( )+ ( )2 (-4x+5y)2 =( )2 +2( )( )+ ( )2
=
(2) (2a+3b ) 2 = ( )2 +2( )( )+ ( )2 利用两数和的平方公式计算: ==7提问:(a-b)2等于什么? 是否可以写成[a+(-b)]2? 你能继续做下去吗?(a-b)2= a2 - 2ab+b28 (a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2 完全平方公式首平方,尾平方,首尾两倍中间放 公式变形为
(首±尾)2=首2±2×首×尾+尾29(a-b)2b2两数差的完全平方公式: (a-b)2= a2 - 2ab+b2的图形理解10例2.计算: (x-2y)2(x - 2y )2=(a - b )2 =a2 - 2 a b + b2x2 - 2· x· 2y +( 2y )2 =x2 - 4xy+4y211做一做 (r-h )2 = ( )2 –2( )( )+ ( )2 (-2x-3y)2 =( )2 –2( )( )+ ( )2
=
(2) ( m-2) 2 = ( )2 –2( )( )+ ( )2 利用两数差的平方公式计算: ==12 例3 用完全平方公式计算:(1)(x+2y)2(2)(2a-5)2(3)(-2s+t)2(4)(-3x-4y)2=X2+4xy+4y2=4a2-20a+25=4s2-4st+t2 =9x2+24xy+16y2思考: (1)完全平方展开有几项?
(2)每一项的符号特征?13
(7-y )2 =比较下列计算结果,你能得到什么结论? (2s-t )2=(-2x-3y )2=(a-b)2= (-a+b )2互为相反数的两个数的完全平方相等(2) (-2s+t)2=(1) (y-7)2 = (3) (2x+3y)2=(-a-b)2= (a+b )214 比较平方差公式和完全平方公式:(a-b)(a+b)= a2-b2( a+ b)2=a2+2 a b+ b2( a- b)2= a2-2 a b+ b2 平方差公式和完全平方公式都叫乘法公式15练一练选择适当的公式计算:
(1)(2x-1)(-1+2x); (2) (-2x-y)(2x-y)
(3) (-a+5)(-a-5); (4) (ab-1)(-ab+1)16 完全平方公式口诀:首平方,尾平方,首尾两倍中间放 我们把两数和的平方公式与两数差的平方公式统称为完全平方公式。(也叫乘法公式)小结在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2;17发散练习,勇于创新1.如果x2-6x+N是一个完全平方式,那么N是( )
(A ) 11 (B) 9 (C) -11 (D) -93.已知(a+b)2=11 , ab=1 , 求(a-b)2的值.B2.如果x2-kx+9是一个完全平方式,那么k是( )
(A ) ±3 (B) 6 (C) -6 (D) ±6 D18(a+b)2 = a2+2ab+b2(a-b)2 = a2-2ab+b219提高题1、计算:2、若 ,则
= 。20a2+b2 =(a+b)2 -2ab21想一想22拓展:
1.计算:
2.已知 求下列各式的值
(1). (2).
