3.1 不等关系与不等式 课件3

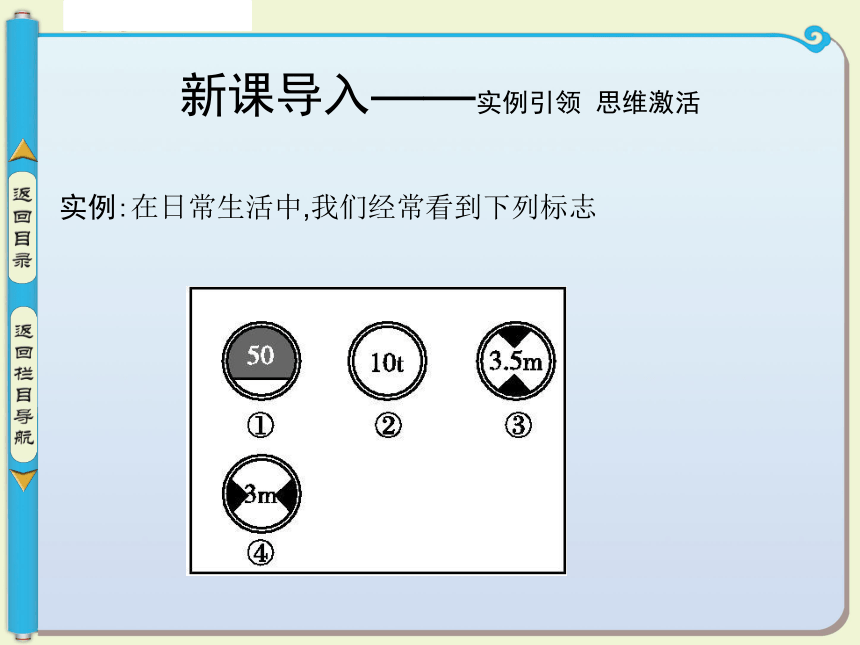
课件27张PPT。3.1 不等关系与不等式新课导入知识探究题型探究达标检测新课导入——实例引领 思维激活实例:在日常生活中,我们经常看到下列标志想一想 图中的标志各表示什么意思?你能用数学关系式表示吗?
(①最低限速:限制行驶时速v不得低于50公里,v≥50;
②限制质量:装载总质量G不得超过10吨,0≤G≤10;
③限制高度:装载高度h不得超过3.5米,0≤h≤3.5;
④限制宽度:装载宽度a不得超过3米,0≤a≤3)知识探究——自主梳理 思考辨析1.比较实数a、b的大小
(1)文字叙述
如果a-b是 ,那么a>b;
如果a-b ,那么a=b;
如果a-b是 ,那么a(2)符号表示
a-b>0?a b;
a-b=0?a b;
a-b<0?a b.正数等于零负数>=c (6)乘法性质: > b(1)对称性:a>b? .(2)传递性: ? .(3)加法性质: ?a+c>b+c. (4)乘法性质: ?ac>bc, ?acb+d. ? .ac>bd (7)乘方性质: ?an>bn. (8)开方性质: ? . 思考:由a>b可以得出 < 吗?
提示:不可以.例如当a=2,b=-2时,该结论错误;当a·b>0时,a>b? <题型探究——典例剖析 举一反三题型一 用不等式来表示不等关系
【例1】 用一段长为30 m的篱笆围成一个一边靠墙的矩形菜园,墙长18 m,要求菜园的面积不小于216 m2,靠墙的一边长为x m.试用不等式表示其中的不等关系.名师导引: (1)矩形菜园靠墙的一边长x应满足什么条件?(0(2)在用不等式表示实际问题时,一定要注意单位统一.跟踪训练1-1:配制A、B两种药剂,需要甲、乙两种原料.已知配一剂A种药需甲料3克,乙料5克;配一剂B种药需甲料5克,乙料4克.今有甲料20克,乙料25克,若A、B两种药至少各配一剂,设A、B两种药分别配x、y剂(x、y∈N),请写出x、y应满足的不等关系式.题型二 作差法比较两式或两数的大小
【例2】 已知x∈R,试比较3x2-2x+1与2x2-x-1的大小.题后反思 (1)比较两个实数(代数式)大小的一般步骤是作差——变形——判断符号——下结论.
(2)作差法比较大小的关键是变形,常用的变形方法有配方、通分、因式分解、分子(或分母)有理化等.跟踪训练2-1:比较下列各组中两个代数式的大小:
(1)x2+3与3x;
(2)已知a,b为正数,且a≠b,比较a3+b3与a2b+ab2.(2)(a3+b3)-(a2b+ab2)
=a3+b3-a2b-ab2
=a2(a-b)-b2(a-b)
=(a-b)(a2-b2)
=(a-b)2(a+b),
∵a>0,b>0且a≠b,
∴(a-b)2>0,a+b>0.
∴(a3+b3)-(a2b+ab2)>0,
即a3+b3>a2b+ab2.跟踪训练3-1:已知a>b,m>n,p>0,求证:n-ap证明:∵a>b,又p>0,∴ap>bp,
∴-ap<-bp,
又m>n,即n(2)要充分利用所给条件,进行适当变形来求范围,注意变形的等价性【例1】设f(x)=ax2+bx,1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围.达标检测——反馈矫正 及时总结1.若a>b,c>d,则下列不等式关系中不一定成立的是(　 　)
(A)a-b>d-c (B)a+d>b+c
(C)a-c>b-c (D)a-c解析:由不等式的性质易知A、C、D成立,选B.B2.设m=x2+y2+2y,n=2x-5,则m,n的大小关系是(　 　)
(A)m>n (B)m(C)m=n (D)与x,y取值有关
解析:m-n=x2+y2+2y-2x+5
=(x-1)2+(y+1)2+3>0,
∴m>n,选A.A3.当x>0时,2x+3与x+2的大小关系为　　　　.?
解析: (2x+3)-(x+2)=x+1,
∵x>0,
∴x+1>1>0,
∴2x+3>x+2.
答案:2x+3>x+24.一辆汽车原来每天行驶x km,如果该汽车每天行驶的路程比原来少10 km,那么在6天内它的行程将不超过2000 km,用不等式表示为　　　　.?
解析:如果该汽车每天行驶的路程比原来少10 km,那么在6天内它的行程为6(x-10)km,那么不等关系“在6天内它的行程将不超过2000 km”可以用不等式6(x-10)≤2000来表示.
答案:6(x-10)≤2000课堂小结
1.比较两个实数的大小,只要考察它们的差就可以了.
a-b>0?a>b;a-b=0?a=b;a-b<0?a2.作差比较的一般步骤:
第一步:作差;第二步:变形,常采用配方、因式分解等恒等变形手段,将“差”化成“积”;第三步:定号,就是确定是大于0,等于0,还是小于0.(不确定的要分情况讨论)最后得结论.概括为“三步一结论”,这里的“定号”是目的,“变形”是关键.
3.不等式的性质是不等式变形的依据,每一步变形都要严格依性质进行,千万不可想当然.