3.2 一元二次不等式及其解法 课件2
文档属性
| 名称 | 3.2 一元二次不等式及其解法 课件2 |  | |
| 格式 | zip | ||
| 文件大小 | 997.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-08 16:34:19 | ||
图片预览






文档简介
课件15张PPT。3.2一元二次不等式的解法1、一元二次不等式
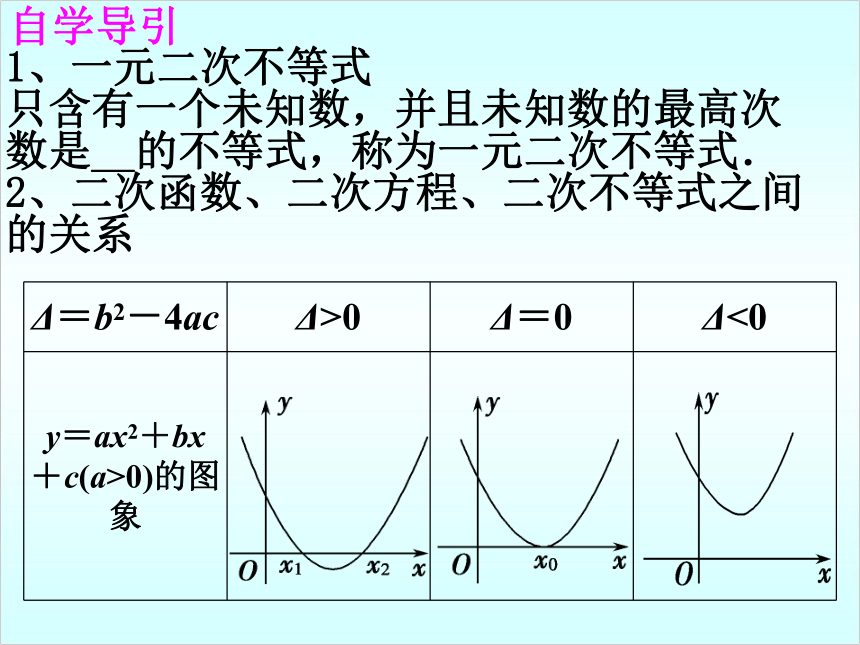
只含有一个未知数,并且未知数的最高次数是__的不等式,称为一元二次不等式.
2、二次函数、二次方程、二次不等式之间的关系自学导引没有实数根{x|xx2} :一元二次不等式ax2+bx+c>0(a≠0)具备哪些条件时,解集为R或??
提示:当a>0,Δ<0时,解集为R.当a<0,Δ≤0时,解集为?.
1、解一元二次不等式的常见方法
(1)图象法:由一元二次方程、一元二次不等式及二次函数的关系,可以得到解一元二次不等式的一般步骤:
①化不等式为标准形式:ax2+bx+c>0(a>0),或ax2+bx+c<0(a>0);
②求方程ax2+bx+c=0(a>0)的根,并画出对应函数y=ax2+bx+c图象的简图;
③由图象得出不等式的解集.
(2)代数法:将所给不等式化为一般式后借助分解因式或配方求解.
当m0,则可得x>n或x若(x-m)(x-n)<0,则可得m名师点睛2、含参数的一元二次型的不等式
在解含参数的一元二次型的不等式时,往往要对参数进行分类讨论,为了做到分类“不重不漏”,讨论需从如下三个方面进行考虑:
(1)关于不等式类型的讨论:二次项系数a>0,a<0,a=0.
(2)关于不等式对应的方程根的讨论:二根(Δ>0),一根
(Δ=0),无根(Δ<0).
(3)关于不等式对应的方程根的大小的讨论:x1>x2,
x1=x2,x1 题型一 一元二次不等式的解法 例1、求下列一元二次不等式的解集.
(1)x2-5x>6;
(2)4x2-4x+1≤0;
(3)-x2+7x>6.
[思路探索] 先将二次项系数化为正,再求对应方程的根.并根据情况结合二次函数图象,写出解集.
解 (1)由x2-5x>6,得x2-5x-6>0.
∴x2-5x-6=0的两根是x=-1或6.
∴原不等式的解集为{x|x<-1或x>6}.
(2)4x2-4x+1≤0,即(2x-1)2≤0,
(3)由-x2+7x>6,得x2-7x+6<0,
而x2-7x+6=0的两个根是x=1或6.
∴不等式x2-7x+6<0的解集为{x|1 当所给不等式是非一般形式的不等式时,应先化为一般形式,在具体求解一个一般形式的一元二次不等式的过程中,要密切结合一元二次方程的根的情况以及二次函数的图象.
解下列不等式
(1)2x2-x+6>0;
(3)(5-x)(x+1)≥0.
解 (1)∵方程2x2-x+6=0的判别式Δ=(-1)2-4×2×6<0,
∴函数y=2x2-x+6的图象开口向上,与x轴无交点.
∴原不等式的解集为R.
(2)原不等式可化为x2-6x+10<0,
∵Δ=62-40=-4<0,
∴原不等式的解集为?.
(3)原不等式可化为(x-5)(x+1)≤0,
所以原不等式的解集为{x|-1≤x≤5}.
【变式1】 已知不等式ax2-bx+2<0的解集为{x|1解 法一 由题设条件知a>0,且1,2是方程ax2-bx+2=0的两实根.
【变式2】 若不等式(a-2)x2+2(a-2)x-4<0的解集为R,求实数a的取值范围. 误区警示 忽略二次项系数为零而出错【示例】 当a-2=0时,原不等式不是一元二次不等式,不能应用根的判别式,应当单独检验不等式是否成立.
正解: 当a-2=0,即a=2时,原不等式为-4<0,
所以a=2时成立.
当a-2≠0时,由题意得
即解得-2综上所述可知:-2 二次项系数含参数时,要严格分系数为正,系数为0,系数为负三种情况进行讨论,缺一不可,只要题目没有明确说明不等式是一元二次不等式,就必须讨论这种情况.1.解一元二次不等式的一般步骤
(1)对不等式变形,使一端为0且二次项系数大于0,即ax2 +bx+c>0(a>0),ax2+bx+c<0(a>0);
(2)计算相应的判别式;
(3)当Δ≥0时,求出相应的一元二次方程的两根;
(4)根据对应二次函数的图象,写出不等式的解集.课程总结2.对于解含有参数的二次不等式,一般讨论的顺序是:
(1)讨论二次项系数是否为0,这决定此不等式是否为二次不等式;
(2)当二次项系数不为0时,讨论判别式是否大于0;
(3)当判别式大于0时,讨论二次项系数是否大于0,这决定所求不等式的不等号的方向;
(4)判断二次不等式两根的大小.
谢谢观看!再见!
只含有一个未知数,并且未知数的最高次数是__的不等式,称为一元二次不等式.
2、二次函数、二次方程、二次不等式之间的关系自学导引没有实数根{x|x
提示:当a>0,Δ<0时,解集为R.当a<0,Δ≤0时,解集为?.
1、解一元二次不等式的常见方法
(1)图象法:由一元二次方程、一元二次不等式及二次函数的关系,可以得到解一元二次不等式的一般步骤:
①化不等式为标准形式:ax2+bx+c>0(a>0),或ax2+bx+c<0(a>0);
②求方程ax2+bx+c=0(a>0)的根,并画出对应函数y=ax2+bx+c图象的简图;
③由图象得出不等式的解集.
(2)代数法:将所给不等式化为一般式后借助分解因式或配方求解.
当m
在解含参数的一元二次型的不等式时,往往要对参数进行分类讨论,为了做到分类“不重不漏”,讨论需从如下三个方面进行考虑:
(1)关于不等式类型的讨论:二次项系数a>0,a<0,a=0.
(2)关于不等式对应的方程根的讨论:二根(Δ>0),一根
(Δ=0),无根(Δ<0).
(3)关于不等式对应的方程根的大小的讨论:x1>x2,
x1=x2,x1
(1)x2-5x>6;
(2)4x2-4x+1≤0;
(3)-x2+7x>6.
[思路探索] 先将二次项系数化为正,再求对应方程的根.并根据情况结合二次函数图象,写出解集.
解 (1)由x2-5x>6,得x2-5x-6>0.
∴x2-5x-6=0的两根是x=-1或6.
∴原不等式的解集为{x|x<-1或x>6}.
(2)4x2-4x+1≤0,即(2x-1)2≤0,
(3)由-x2+7x>6,得x2-7x+6<0,
而x2-7x+6=0的两个根是x=1或6.
∴不等式x2-7x+6<0的解集为{x|1
解下列不等式
(1)2x2-x+6>0;
(3)(5-x)(x+1)≥0.
解 (1)∵方程2x2-x+6=0的判别式Δ=(-1)2-4×2×6<0,
∴函数y=2x2-x+6的图象开口向上,与x轴无交点.
∴原不等式的解集为R.
(2)原不等式可化为x2-6x+10<0,
∵Δ=62-40=-4<0,
∴原不等式的解集为?.
(3)原不等式可化为(x-5)(x+1)≤0,
所以原不等式的解集为{x|-1≤x≤5}.
【变式1】 已知不等式ax2-bx+2<0的解集为{x|1
【变式2】 若不等式(a-2)x2+2(a-2)x-4<0的解集为R,求实数a的取值范围. 误区警示 忽略二次项系数为零而出错【示例】 当a-2=0时,原不等式不是一元二次不等式,不能应用根的判别式,应当单独检验不等式是否成立.
正解: 当a-2=0,即a=2时,原不等式为-4<0,
所以a=2时成立.
当a-2≠0时,由题意得
即解得-2
(1)对不等式变形,使一端为0且二次项系数大于0,即ax2 +bx+c>0(a>0),ax2+bx+c<0(a>0);
(2)计算相应的判别式;
(3)当Δ≥0时,求出相应的一元二次方程的两根;
(4)根据对应二次函数的图象,写出不等式的解集.课程总结2.对于解含有参数的二次不等式,一般讨论的顺序是:
(1)讨论二次项系数是否为0,这决定此不等式是否为二次不等式;
(2)当二次项系数不为0时,讨论判别式是否大于0;
(3)当判别式大于0时,讨论二次项系数是否大于0,这决定所求不等式的不等号的方向;
(4)判断二次不等式两根的大小.
谢谢观看!再见!
