3.2 一元二次不等式及其解法 课件4
文档属性
| 名称 | 3.2 一元二次不等式及其解法 课件4 |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-08 16:36:17 | ||
图片预览






文档简介
课件26张PPT。 第三章 不等式
3.2 一元二次不等式及其解法例如下面的不等式:
15x2+30x-1>0 和 3x2+6x-1≤0.一元二次不等式有两个共同特点: (1)含有一个未知数x;
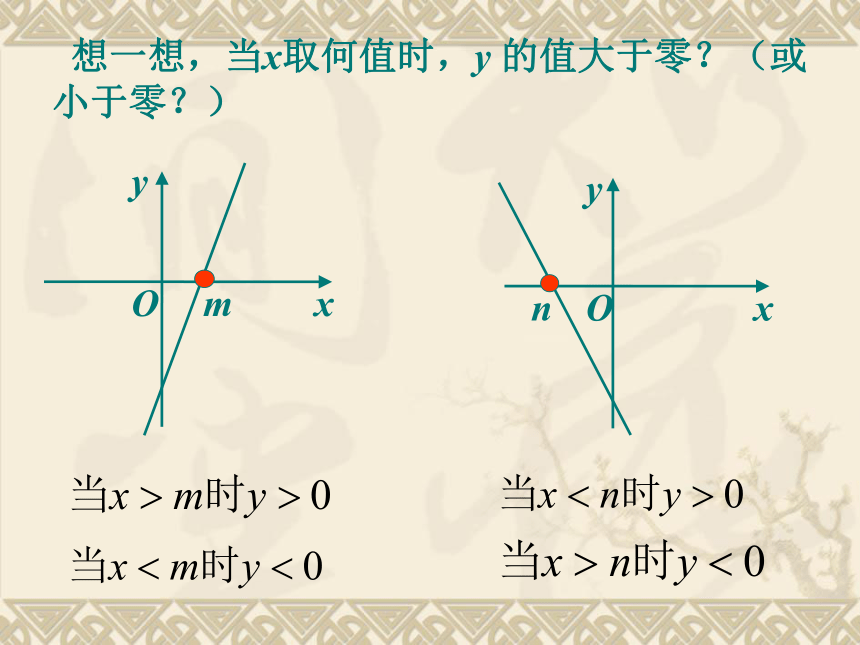
(2)未知数的最高次数为2. 一般地,含有一个未知数,且未知数的最高次数为2的整式不等式,叫做一元二次不等式。问题:如何解一元二次不等式呢? 考察:对一次函数y=2x-7,当x为何值时,y=0;当x为何值时,y<0;当x为何值时,y>0?当x=3.5时,2x-7=0,
即 y=0;
当x<3.5时,2x-7<0,
即 y<0;
当x>3.5时,2x-7>0,
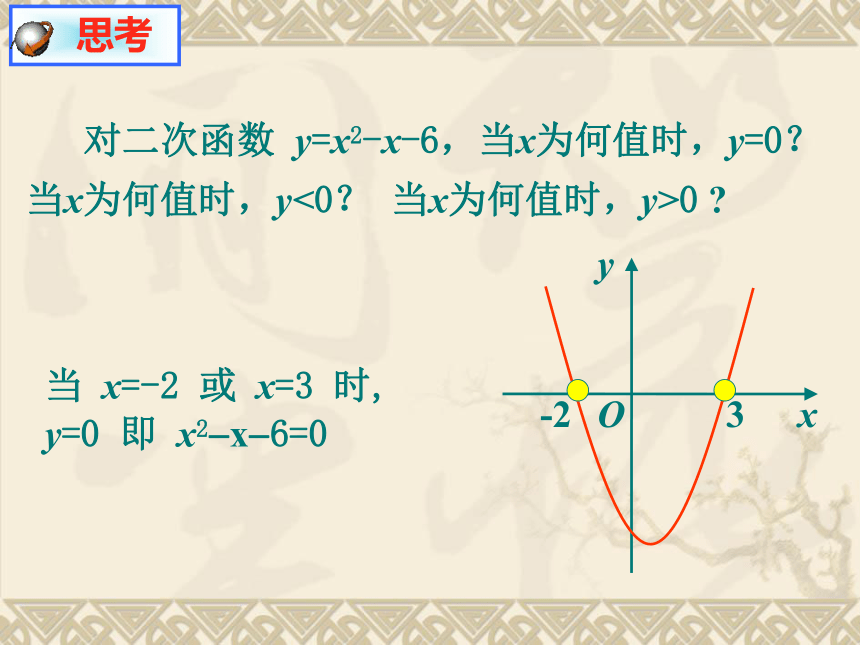
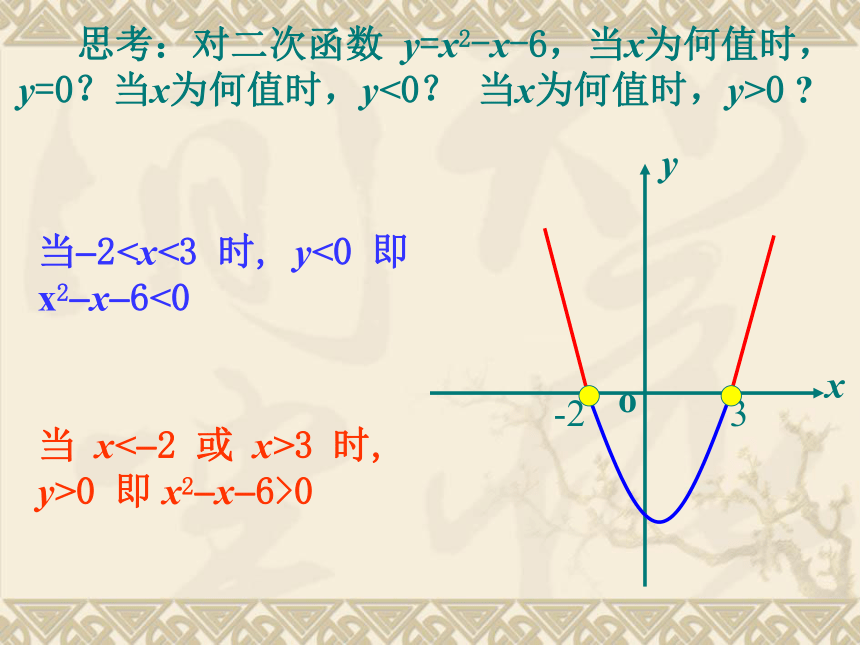
即 y>0 想一想,当x取何值时,y 的值大于零?(或小于零?) 对二次函数 y=x2-x-6,当x为何值时,y=0?当x为何值时,y<0? 当x为何值时,y>0 ? 思考当 x=-2 或 x=3 时, y=0 即 x2?x?6=0 思考:对二次函数 y=x2-x-6,当x为何值时,y=0?当x为何值时,y<0? 当x为何值时,y>0 ?当 x3 时, y>0 即 x2?x?6>0当?2 一元二次方程、二次函数、一元二次不等式三者之间存在怎样的联系我们可以利用二次函数图象解一元二次不等式.若一元二次方程x2-x-6=0
的解是x1=-2,x2=3. 则抛物线y=x2-x-6与
x轴的交点就是
(-2,0)与(3,0), 一元二次不等式
x2-x-6<0 的解集是 {x|-2 x2-x-6>0 的解集是 {x|x<-2或x>3}.y=x2-x-6问:二次函数y= ax2+bx+c(a>0)
与x轴的交点情况有哪几种? Δ>0 Δ=0 Δ<0x1=x2利用二次函数图象能解一元二次不等式! ==< < > > 练习.解不等式 2x2-3x-2 > 0 .解:因为△ =(-3)2-4×2×(-2)>0,所以方程2x2-3x-2 =0的解是所以,原不等式的解集是先求方程的根然后想像图象形状若改为:不等式 2x2-3x-2 < 0 .总结: 解一元二次不等式 ax2+bx+c>0 (a>0,△≥0 )的步骤: ① 将二次不等式化成一般式(a>0 ); ② 求出方程ax2+bx+c=0的两根;④ 根据图象写出不等式的解集. ③ 画出y=ax2+bx+c的图象;思考:
如何求一元二次
不等式x2-7x+6 > 0
的解集?(-∞,1)(1,6)(6,+∞)xyy=x2-7x+6△>0有两相异实根
x1, x2 (x1x2}{x|x1< x x1=x2={x|x≠ }ΦΦR没有实根一元二次不等式的解法课堂小结: 这张表是我们今后求解一元二次不等式的主要工具,必须熟练掌握,其关键是抓住相应的二次函数的图像。记忆口诀:
大于取两边,小于取中间.求解一元二次不等式ax2+bx+c>0
(a>0)的程序框图(本节课本):x< x1或x> x2例1.解不等式 4x2-4x+1 > 0 解:因为△ =0,方程4x2-4x+1 =0的解是所以,原不等式的解集是注:4x2-4x+1 <0例2、-x2 +2x -3>0-x2 +2x -3>0图象如右图:再次强调注意公式口诀的大前提:a>0a>0 解:设这辆车刹车前的车速至少为xkm/h,根据题意,我们得到
移项整理,得
例3、某种汽车在水泥路面上的刹车距离s(米)和汽车车速x(千米/小时)有如下关系,
在一次交通事故测得这种车的刹车距离大于39.5m,那么这辆车刹车前的车速至少是多少?(精确到0.01km/h) 在这个实际问题中,x>0,所以这辆车刹车的车速至少为79.94km/h。例3、某种汽车在水泥路面上的刹车距离s(米)和汽车车速x(千米/小时)有如下关系,
在一次交通事故测得这种车的刹车距离大于39.5m,那么这辆车刹车前的车速至少是多少?(精确到0.01km/h)移项整理,得 例4 一个车辆制造厂引进了一条摩托车整车装配流水线,这条流水线生产的摩托车数量x(辆)与创造的价值 y(元)之间有如下的关系: y = -2 x2 + 220x. 若这家工厂希望在一个星期内利用这条流水线创收6000元以上,那么它在一个星期内大约应该生产多少辆摩托车? 解:设在一个星期内大约应该生产x辆摩托车.根据题意,得到 -2x2 + 220x > 6000
移项整理,得 x2 - 110x + 3000 < 0.
因为△=100>0,所以方程 x2-110x+3000=0有两个实数根x1=50, x2=60. 解:设在一个星期内大约应该生产x辆摩托车.根据题意,得到 -2x2 + 220x > 6000
移项整理,得 x2 - 110x + 3000 < 0.
因为△=100>0,所以方程 x2-110x+3000=0有两个实数根
x1=50, x2=60.
由函数y=x2-110x+3000的图象,
得不等式的解为50 因为x只能取整数,所以当这条摩托
车整车装配流水线在一周内生产的摩托
车数量在51辆到59辆之间时,这家工厂
能够获得6000元以上的收益.
3.2 一元二次不等式及其解法例如下面的不等式:
15x2+30x-1>0 和 3x2+6x-1≤0.一元二次不等式有两个共同特点: (1)含有一个未知数x;
(2)未知数的最高次数为2. 一般地,含有一个未知数,且未知数的最高次数为2的整式不等式,叫做一元二次不等式。问题:如何解一元二次不等式呢? 考察:对一次函数y=2x-7,当x为何值时,y=0;当x为何值时,y<0;当x为何值时,y>0?当x=3.5时,2x-7=0,
即 y=0;
当x<3.5时,2x-7<0,
即 y<0;
当x>3.5时,2x-7>0,
即 y>0 想一想,当x取何值时,y 的值大于零?(或小于零?) 对二次函数 y=x2-x-6,当x为何值时,y=0?当x为何值时,y<0? 当x为何值时,y>0 ? 思考当 x=-2 或 x=3 时, y=0 即 x2?x?6=0 思考:对二次函数 y=x2-x-6,当x为何值时,y=0?当x为何值时,y<0? 当x为何值时,y>0 ?当 x3 时, y>0 即 x2?x?6>0当?2
的解是x1=-2,x2=3. 则抛物线y=x2-x-6与
x轴的交点就是
(-2,0)与(3,0), 一元二次不等式
x2-x-6<0 的解集是 {x|-2
与x轴的交点情况有哪几种? Δ>0 Δ=0 Δ<0x1=x2利用二次函数图象能解一元二次不等式! ==< < > > 练习.解不等式 2x2-3x-2 > 0 .解:因为△ =(-3)2-4×2×(-2)>0,所以方程2x2-3x-2 =0的解是所以,原不等式的解集是先求方程的根然后想像图象形状若改为:不等式 2x2-3x-2 < 0 .总结: 解一元二次不等式 ax2+bx+c>0 (a>0,△≥0 )的步骤: ① 将二次不等式化成一般式(a>0 ); ② 求出方程ax2+bx+c=0的两根;④ 根据图象写出不等式的解集. ③ 画出y=ax2+bx+c的图象;思考:
如何求一元二次
不等式x2-7x+6 > 0
的解集?(-∞,1)(1,6)(6,+∞)xyy=x2-7x+6△>0有两相异实根
x1, x2 (x1
大于取两边,小于取中间.求解一元二次不等式ax2+bx+c>0
(a>0)的程序框图(本节课本):x< x1或x> x2例1.解不等式 4x2-4x+1 > 0 解:因为△ =0,方程4x2-4x+1 =0的解是所以,原不等式的解集是注:4x2-4x+1 <0例2、-x2 +2x -3>0-x2 +2x -3>0图象如右图:再次强调注意公式口诀的大前提:a>0a>0 解:设这辆车刹车前的车速至少为xkm/h,根据题意,我们得到
移项整理,得
例3、某种汽车在水泥路面上的刹车距离s(米)和汽车车速x(千米/小时)有如下关系,
在一次交通事故测得这种车的刹车距离大于39.5m,那么这辆车刹车前的车速至少是多少?(精确到0.01km/h) 在这个实际问题中,x>0,所以这辆车刹车的车速至少为79.94km/h。例3、某种汽车在水泥路面上的刹车距离s(米)和汽车车速x(千米/小时)有如下关系,
在一次交通事故测得这种车的刹车距离大于39.5m,那么这辆车刹车前的车速至少是多少?(精确到0.01km/h)移项整理,得 例4 一个车辆制造厂引进了一条摩托车整车装配流水线,这条流水线生产的摩托车数量x(辆)与创造的价值 y(元)之间有如下的关系: y = -2 x2 + 220x. 若这家工厂希望在一个星期内利用这条流水线创收6000元以上,那么它在一个星期内大约应该生产多少辆摩托车? 解:设在一个星期内大约应该生产x辆摩托车.根据题意,得到 -2x2 + 220x > 6000
移项整理,得 x2 - 110x + 3000 < 0.
因为△=100>0,所以方程 x2-110x+3000=0有两个实数根x1=50, x2=60. 解:设在一个星期内大约应该生产x辆摩托车.根据题意,得到 -2x2 + 220x > 6000
移项整理,得 x2 - 110x + 3000 < 0.
因为△=100>0,所以方程 x2-110x+3000=0有两个实数根
x1=50, x2=60.
由函数y=x2-110x+3000的图象,
得不等式的解为50
车整车装配流水线在一周内生产的摩托
车数量在51辆到59辆之间时,这家工厂
能够获得6000元以上的收益.
