3.3.1 二元一次不等式(组)与平面区域 课件2
文档属性
| 名称 | 3.3.1 二元一次不等式(组)与平面区域 课件2 |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-08 16:39:30 | ||
图片预览






文档简介
课件14张PPT。 第三章 不等式
3.3.1 二元一次不等式(组)与平面区域实 例 ----- 一家银行的信贷部计划年初投入25 000 000元用于企业投资和个人贷款,希望这笔资金至少可带来30 000元的收益,其中从企业贷款中获益12﹪,从个人贷款中获益10﹪,那么,信贷部应该如何分配资金呢?分配资金应该满足的条件为①②③④ 满足二元一次不等式(组)的x与y的取值构成有序实数对(x, y),所有这样的有序实数对构成的集合称为二元一次不等式(组)的解集。 有序实数对可以看成直角坐标系内点的坐标。于是,二元一次不等式(组)的解集就可以看成直角坐标系内的点的构成的集合。思考------二元一次不等式在直角坐标系中所表示的图形?先研究一个具体的二元一次不等式
x-y<6
的解集所表示的图形。x 平面内所有的点被直线x-y=6分成三类:
在直线x-y=6上的点;
在直线x-y=6左上方的区域内的点;
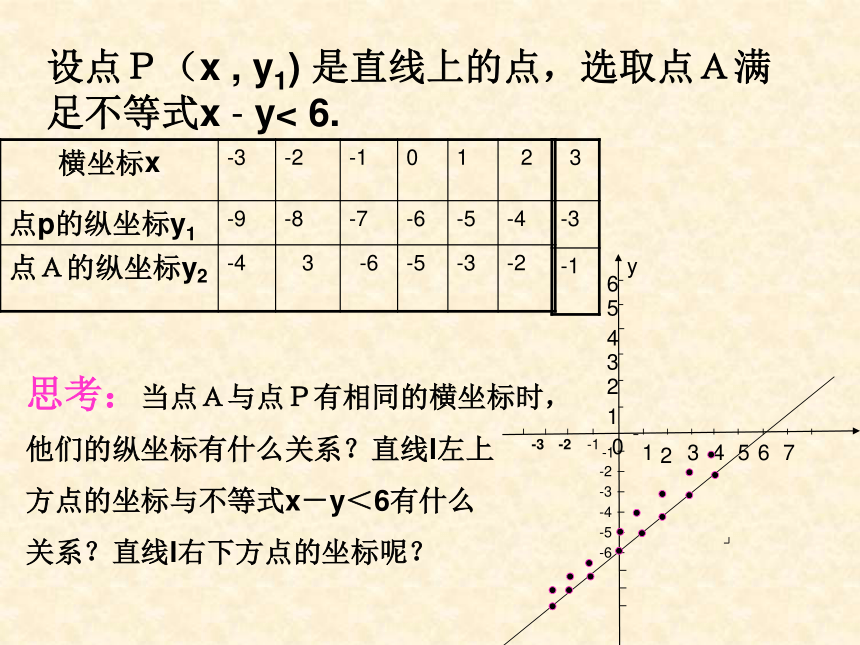
在直线x-y=6右下方的区域内的点。思考:当点A与点P有相同的横坐标时,
他们的纵坐标有什么关系?直线l左上
方点的坐标与不等式x-y<6有什么
关系?直线l右下方点的坐标呢?设点P(x , y1) 是直线上的点,选取点A满足不等式x - y< 6.12435761234560y-3-2-1-1-2-3-4-5-6 在平面直角坐标系中,以二元一次不等式x-y < 6的解为坐标的点都在直线l的左上方 不等式 x-y < 6表示直线 x- y = 6 左上方的平面区域二元一次不等式x-y>6表示直线x- y=6右下方的平面区域直线x- y=6叫做这两个区域的 边 界注意:这里我们把直线x- y=6化成虚线,以表示区域不包括边界。注意:(1) 一般的,在平面直角坐标系中,二元一次不等式
A x+ B y+ C>0
表示直线A x+ B y+ C=0某一侧所有点组成的平面区域。我们把直线画成虚线,以表示区域不包括边界. (2) 不等式A x+ B y+ C≥0表示的平面区域包括边界,把边界画成实现. 对于直线A x+ B y+ C=0同一侧的所有点,把它的坐标(x, y)待入 A x+ B y+ C,所得符号都相同,所以只需在直线的同一侧取某个特殊点(x0,y0)作为测试点,由所得符号确定A x+ B y+ C>0在哪 一侧.
判断方法:例1、画出不等式 x + 4y < 4 表示的平面区域。解:先作出边界 x+4y = 4,因为这条线上的点都不满足x+4y<4,所以画成虚线取原点(0,0),代入x+4y-4,因为0+4×0-4 = - 4<0所以原点(0,0)在x+4y-4<0表示的平面区域内,不等式x+4y<4表示的平面区域在直线x+4y=4 的左下方。x+4y<4练习----1、不等式x-2y+6>0表示的平面区域在直线的x -2y+6=0的( )
右上方 B. 右下方
C、左上方 D、左下方2、不等式3x+2y-6≤0表示的平面区域是( )ABCDXYxyxyxyxDB归纳-----对于直线Ax + By + C = O(1)若A>0,B<0Ax+By+C<0在左上方Ax +B y+ C>0在右下方(2)A>0,B>0Ax +B y+ C>0在右上方Ax+By+C<0在左下方例 2、用平面 区域表示不等式组y<-3x+12
x<2y的解集。分析:由于所求平面区域的点的坐标要同时满足两个不等式,因此二元一次不等式组所表示的平面区域是各个不等式表示的平面区域的交集,即各个不等式表示的平面区域的公共部分。解:不等式y<-3x+12即3x+ y-12<0,表示的平面区域在直线3x+ y-12=0的左下方;不等式x<2y即x-2y<0,表示的是直线x-2y=0的左上方的区域取两区域重叠的部分,即阴影部分就表示原不等式组的解集例3 、要将两种大小不同的钢板截成A.B.C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示:规格类型钢板类型今需要A.B.C三种规格的成品分别为15,18,27块,用数学关系式和图形表示上述要求。解:设需要截第一种钢板x张,第二种
钢板y张,则2x+y≥15X+2y≥18X+3y ≥27x ≥0y ≥00246810121416182022242628246810121416182x+y=15X+2y=18X+3y=27例4、一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4t,硝酸盐18;生产1车皮乙种肥料需要的主要原料是磷酸盐1t,硝酸盐15t。现库存磷酸盐10t,硝酸盐66t,在此基础上生产这两种混合肥料。列出满足生产条件的数学关系式,并画出相应的平面区域。解:设x,y分别为计划生产甲、乙两种
混合肥料的车皮数,于是满足以下条件4x+y≤1018x+15y ≤66x≥0y ≥04x+y=1018x+15y =66
3.3.1 二元一次不等式(组)与平面区域实 例 ----- 一家银行的信贷部计划年初投入25 000 000元用于企业投资和个人贷款,希望这笔资金至少可带来30 000元的收益,其中从企业贷款中获益12﹪,从个人贷款中获益10﹪,那么,信贷部应该如何分配资金呢?分配资金应该满足的条件为①②③④ 满足二元一次不等式(组)的x与y的取值构成有序实数对(x, y),所有这样的有序实数对构成的集合称为二元一次不等式(组)的解集。 有序实数对可以看成直角坐标系内点的坐标。于是,二元一次不等式(组)的解集就可以看成直角坐标系内的点的构成的集合。思考------二元一次不等式在直角坐标系中所表示的图形?先研究一个具体的二元一次不等式
x-y<6
的解集所表示的图形。x 平面内所有的点被直线x-y=6分成三类:
在直线x-y=6上的点;
在直线x-y=6左上方的区域内的点;
在直线x-y=6右下方的区域内的点。思考:当点A与点P有相同的横坐标时,
他们的纵坐标有什么关系?直线l左上
方点的坐标与不等式x-y<6有什么
关系?直线l右下方点的坐标呢?设点P(x , y1) 是直线上的点,选取点A满足不等式x - y< 6.12435761234560y-3-2-1-1-2-3-4-5-6 在平面直角坐标系中,以二元一次不等式x-y < 6的解为坐标的点都在直线l的左上方 不等式 x-y < 6表示直线 x- y = 6 左上方的平面区域二元一次不等式x-y>6表示直线x- y=6右下方的平面区域直线x- y=6叫做这两个区域的 边 界注意:这里我们把直线x- y=6化成虚线,以表示区域不包括边界。注意:(1) 一般的,在平面直角坐标系中,二元一次不等式
A x+ B y+ C>0
表示直线A x+ B y+ C=0某一侧所有点组成的平面区域。我们把直线画成虚线,以表示区域不包括边界. (2) 不等式A x+ B y+ C≥0表示的平面区域包括边界,把边界画成实现. 对于直线A x+ B y+ C=0同一侧的所有点,把它的坐标(x, y)待入 A x+ B y+ C,所得符号都相同,所以只需在直线的同一侧取某个特殊点(x0,y0)作为测试点,由所得符号确定A x+ B y+ C>0在哪 一侧.
判断方法:例1、画出不等式 x + 4y < 4 表示的平面区域。解:先作出边界 x+4y = 4,因为这条线上的点都不满足x+4y<4,所以画成虚线取原点(0,0),代入x+4y-4,因为0+4×0-4 = - 4<0所以原点(0,0)在x+4y-4<0表示的平面区域内,不等式x+4y<4表示的平面区域在直线x+4y=4 的左下方。x+4y<4练习----1、不等式x-2y+6>0表示的平面区域在直线的x -2y+6=0的( )
右上方 B. 右下方
C、左上方 D、左下方2、不等式3x+2y-6≤0表示的平面区域是( )ABCDXYxyxyxyxDB归纳-----对于直线Ax + By + C = O(1)若A>0,B<0Ax+By+C<0在左上方Ax +B y+ C>0在右下方(2)A>0,B>0Ax +B y+ C>0在右上方Ax+By+C<0在左下方例 2、用平面 区域表示不等式组y<-3x+12
x<2y的解集。分析:由于所求平面区域的点的坐标要同时满足两个不等式,因此二元一次不等式组所表示的平面区域是各个不等式表示的平面区域的交集,即各个不等式表示的平面区域的公共部分。解:不等式y<-3x+12即3x+ y-12<0,表示的平面区域在直线3x+ y-12=0的左下方;不等式x<2y即x-2y<0,表示的是直线x-2y=0的左上方的区域取两区域重叠的部分,即阴影部分就表示原不等式组的解集例3 、要将两种大小不同的钢板截成A.B.C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示:规格类型钢板类型今需要A.B.C三种规格的成品分别为15,18,27块,用数学关系式和图形表示上述要求。解:设需要截第一种钢板x张,第二种
钢板y张,则2x+y≥15X+2y≥18X+3y ≥27x ≥0y ≥00246810121416182022242628246810121416182x+y=15X+2y=18X+3y=27例4、一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4t,硝酸盐18;生产1车皮乙种肥料需要的主要原料是磷酸盐1t,硝酸盐15t。现库存磷酸盐10t,硝酸盐66t,在此基础上生产这两种混合肥料。列出满足生产条件的数学关系式,并画出相应的平面区域。解:设x,y分别为计划生产甲、乙两种
混合肥料的车皮数,于是满足以下条件4x+y≤1018x+15y ≤66x≥0y ≥04x+y=1018x+15y =66
