3.3.1 二元一次不等式(组)与平面区域 课件3
文档属性
| 名称 | 3.3.1 二元一次不等式(组)与平面区域 课件3 |
|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-08 00:00:00 | ||
图片预览







文档简介
课件27张PPT。3.3.1 二元一次不等式(组)与平面区域新课导入知识探究题型探究达标检测新课导入——实例引领 思维激活实例:给出以下两个方程:
①2x+3y-6=0,②x-4y+4=0.想一想 (1)这两个方程是什么类型的方程?它们的解有多少个?它们对应的几何图形是什么?
(都是二元一次方程;都有无穷多解;对应的几何图形是直线)
(2)若将方程中的等号改为不等号,将得到什么?它们有什么
特点?
(将等号改为不等号,将得到不等式;其中都含有2个未知数,未知数的次数都是1)知识探究——自主梳理 思考辨析1.二元一次不等式(组)的概念
(1)二元一次不等式:我们把含有两个未知数,并且未知数的次数是1的不等式称为二元一次不等式.
(2)二元一次不等式组:由几个二元一次不等式组成的不等式组称为二元一次不等式组.
(3)二元一次不等式(组)的解集:满足二元一次不等式(组)的x和y的取值构成 ,所有这样的 构成的集合称为二元一次不等式(组)的解集.有序数对(x,y)有序数对(x,y)2.二元一次不等式表示的平面区域
在平面直角坐标系中,二元一次不等式Ax+By+C>0表示直线Ax+By+C=0某一侧所有点组成的平面区域.我们把直线画成
,以表示区域不包括边界.虚线3.二元一次不等式表示的平面区域的确定
对于直线Ax+By+C=0同一侧的所有点,把它的坐标(x,y)代入Ax+By+C,所得的符号都相同,因此只需在直线Ax+By+C=0的同一侧取某个特殊点(x0,y0)作为测试点,由Ax0+By0+C的符号就可以断定Ax+By+C>0表示的是直线Ax+By+C=0哪一侧的平面区域.
思考:若已知直线l:Ax+By+C=0,记f(x,y)=Ax+By+C,设M(x1,y1),N(x2,y2),那么M与N在直线l同侧的条件是什么?M与N在l两侧的条件是什么?
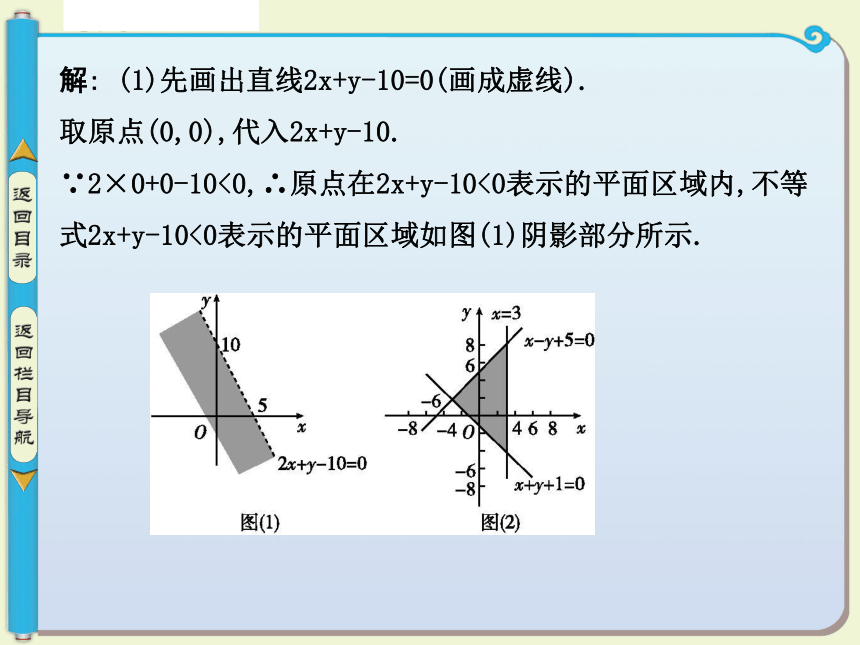
提示:点M与N在l同侧的条件是f(x1,y1)·f(x2,y2)>0;在l异侧的条件是f(x1,y1)·f(x2,y2)<0题型探究——典例剖析 举一反三解: (1)先画出直线2x+y-10=0(画成虚线).
取原点(0,0),代入2x+y-10.
∵2×0+0-10<0,∴原点在2x+y-10<0表示的平面区域内,不等式2x+y-10<0表示的平面区域如图(1)阴影部分所示.(2)不等式x-y+5≥0表示直线x-y+5=0上及右下方的点的集合;x+y+1≥0表示直线x+y+1=0上及右上方的点的集合;x≤3表示直线x=3上及左方的点的集合.所以不等式组表示的平面区域如图(2)阴影部分所示.题后反思 (1)在画二元一次不等式(组)表示的平面区域时,注意区分边界的虚实.Ax+By+C≥0(≤0)表示的平面区域包括直线Ax+By+C=0,该直线要画成实线;Ax+By+C>0(<0)表示的平面区域不包括直线Ax+By+C=0,该直线要画成
虚线.
(2)测试点选取要恰当.一般地选原点(0,0)、(0,1)或(1,0),如果测试点的坐标满足不等式,则所求平面区域为包括测试点的直线的一侧,否则在直线的另一侧,最后将平面区域用阴影表示出来.跟踪训练1-1:如图,请写出表示阴影部分区域的不等式组.解:由于直线BC的方程为y=-1,
直线AC的方程为x=0,
直线AB的方程为
2x-y+2=0,
因此表示该区域的不等式组是题型二 二元一次不等式(组)表示的平面区域的面积与整点个数问题解:画出平面区域如图阴影部分所示,平面区域图形为直角三角形.题型三 实际应用
【例3】 一工厂生产甲、乙两种产品,生产每种1 t产品的资源需求如下表:该厂有工人200人,每天只能保证160 kW·h的用电额度,每天用煤不得超过150 t,请在平面直角坐标系中画出每天甲、乙两种产品允许的产量的范围.名师导引: (1)该工厂每天甲、乙两种产品的产量x,y应受到哪几个方面的限制?(生产两种产品所需的电力之和不能超过160 kW·h,工人人数之和不能超过200人,所需煤之和不能超过150 t)(2)产量x、y本身还应满足什么条件?(x≥0,y≥0)
(3)怎样画出允许的产量的范围的图形?(先确定x、y满足的不等式)解:设每天分别生产甲、乙两种产品xt和yt,生产xt甲产品和yt乙产品的用电量是(2x+8y) kW·h,根据条件,有2x+8y≤160;用煤量为(3x+5y)t,根据条件有3x+5y≤150;用工人数为5x+2y≤200;
另外,还有x≥0,y≥0.甲、乙两种产品的产量范围是这组不等式表示的平面区域,即如图所示的阴影部分(含边界):跟踪训练3-1:某厂使用两种零件A、B装配甲、乙两种产品,该厂的生产能力是每月生产甲产品最多2500件,每月生产乙产品最多1200件,而且装一件甲产品需要4个A,6个B,装一件乙产品需要6个A,8个B,该厂每月能用的A最多有14000个,B最多有12000个,用不等式组将甲、乙两种产品产量之间的关系表示出来,并画出相应的平面区域.备选例题达标检测——反馈矫正 及时总结解析:把三点坐标代入可知,P2、P3满足不等式.故选C.C 2.已知点(3,1)和(-4,6)在直线3x-2y+a=0的异侧,则a的取值范围是 .?
解析:由题意知
(3×3-2×1+a)·[3×(-4)-2×6+a]<0,
即(7+a)(a-24)<0,
解得-7答案: (-7,24)4.根据下列平面区域,写出它们所对应的二元一次不等式(组).(1)平面区域对应的不等式(组): ;?
(2)平面区域对应的不等式(组): ;?
(3)平面区域对应的不等式(组): .?课堂小结
1.一般地,二元一次不等式Ax+By+C>0或Ax+By+C<0在平面直角坐标系内表示直线Ax+By+C=0某一侧的所有点组成的平面区域.
2.在画二元一次不等式表示的平面区域时,应用“直线定边界,特殊点定区域”的方法来画区域,取点时,若直线不过原点,一般用“原点定区域”;若直线过原点,则取点(1,0)即可.总之,尽量减少运算量.
3.画平面区域时,注意边界线的虚实问题.
①2x+3y-6=0,②x-4y+4=0.想一想 (1)这两个方程是什么类型的方程?它们的解有多少个?它们对应的几何图形是什么?
(都是二元一次方程;都有无穷多解;对应的几何图形是直线)
(2)若将方程中的等号改为不等号,将得到什么?它们有什么
特点?
(将等号改为不等号,将得到不等式;其中都含有2个未知数,未知数的次数都是1)知识探究——自主梳理 思考辨析1.二元一次不等式(组)的概念
(1)二元一次不等式:我们把含有两个未知数,并且未知数的次数是1的不等式称为二元一次不等式.
(2)二元一次不等式组:由几个二元一次不等式组成的不等式组称为二元一次不等式组.
(3)二元一次不等式(组)的解集:满足二元一次不等式(组)的x和y的取值构成 ,所有这样的 构成的集合称为二元一次不等式(组)的解集.有序数对(x,y)有序数对(x,y)2.二元一次不等式表示的平面区域
在平面直角坐标系中,二元一次不等式Ax+By+C>0表示直线Ax+By+C=0某一侧所有点组成的平面区域.我们把直线画成
,以表示区域不包括边界.虚线3.二元一次不等式表示的平面区域的确定
对于直线Ax+By+C=0同一侧的所有点,把它的坐标(x,y)代入Ax+By+C,所得的符号都相同,因此只需在直线Ax+By+C=0的同一侧取某个特殊点(x0,y0)作为测试点,由Ax0+By0+C的符号就可以断定Ax+By+C>0表示的是直线Ax+By+C=0哪一侧的平面区域.
思考:若已知直线l:Ax+By+C=0,记f(x,y)=Ax+By+C,设M(x1,y1),N(x2,y2),那么M与N在直线l同侧的条件是什么?M与N在l两侧的条件是什么?
提示:点M与N在l同侧的条件是f(x1,y1)·f(x2,y2)>0;在l异侧的条件是f(x1,y1)·f(x2,y2)<0题型探究——典例剖析 举一反三解: (1)先画出直线2x+y-10=0(画成虚线).
取原点(0,0),代入2x+y-10.
∵2×0+0-10<0,∴原点在2x+y-10<0表示的平面区域内,不等式2x+y-10<0表示的平面区域如图(1)阴影部分所示.(2)不等式x-y+5≥0表示直线x-y+5=0上及右下方的点的集合;x+y+1≥0表示直线x+y+1=0上及右上方的点的集合;x≤3表示直线x=3上及左方的点的集合.所以不等式组表示的平面区域如图(2)阴影部分所示.题后反思 (1)在画二元一次不等式(组)表示的平面区域时,注意区分边界的虚实.Ax+By+C≥0(≤0)表示的平面区域包括直线Ax+By+C=0,该直线要画成实线;Ax+By+C>0(<0)表示的平面区域不包括直线Ax+By+C=0,该直线要画成
虚线.
(2)测试点选取要恰当.一般地选原点(0,0)、(0,1)或(1,0),如果测试点的坐标满足不等式,则所求平面区域为包括测试点的直线的一侧,否则在直线的另一侧,最后将平面区域用阴影表示出来.跟踪训练1-1:如图,请写出表示阴影部分区域的不等式组.解:由于直线BC的方程为y=-1,
直线AC的方程为x=0,
直线AB的方程为
2x-y+2=0,
因此表示该区域的不等式组是题型二 二元一次不等式(组)表示的平面区域的面积与整点个数问题解:画出平面区域如图阴影部分所示,平面区域图形为直角三角形.题型三 实际应用
【例3】 一工厂生产甲、乙两种产品,生产每种1 t产品的资源需求如下表:该厂有工人200人,每天只能保证160 kW·h的用电额度,每天用煤不得超过150 t,请在平面直角坐标系中画出每天甲、乙两种产品允许的产量的范围.名师导引: (1)该工厂每天甲、乙两种产品的产量x,y应受到哪几个方面的限制?(生产两种产品所需的电力之和不能超过160 kW·h,工人人数之和不能超过200人,所需煤之和不能超过150 t)(2)产量x、y本身还应满足什么条件?(x≥0,y≥0)
(3)怎样画出允许的产量的范围的图形?(先确定x、y满足的不等式)解:设每天分别生产甲、乙两种产品xt和yt,生产xt甲产品和yt乙产品的用电量是(2x+8y) kW·h,根据条件,有2x+8y≤160;用煤量为(3x+5y)t,根据条件有3x+5y≤150;用工人数为5x+2y≤200;
另外,还有x≥0,y≥0.甲、乙两种产品的产量范围是这组不等式表示的平面区域,即如图所示的阴影部分(含边界):跟踪训练3-1:某厂使用两种零件A、B装配甲、乙两种产品,该厂的生产能力是每月生产甲产品最多2500件,每月生产乙产品最多1200件,而且装一件甲产品需要4个A,6个B,装一件乙产品需要6个A,8个B,该厂每月能用的A最多有14000个,B最多有12000个,用不等式组将甲、乙两种产品产量之间的关系表示出来,并画出相应的平面区域.备选例题达标检测——反馈矫正 及时总结解析:把三点坐标代入可知,P2、P3满足不等式.故选C.C 2.已知点(3,1)和(-4,6)在直线3x-2y+a=0的异侧,则a的取值范围是 .?
解析:由题意知
(3×3-2×1+a)·[3×(-4)-2×6+a]<0,
即(7+a)(a-24)<0,
解得-7
(2)平面区域对应的不等式(组): ;?
(3)平面区域对应的不等式(组): .?课堂小结
1.一般地,二元一次不等式Ax+By+C>0或Ax+By+C<0在平面直角坐标系内表示直线Ax+By+C=0某一侧的所有点组成的平面区域.
2.在画二元一次不等式表示的平面区域时,应用“直线定边界,特殊点定区域”的方法来画区域,取点时,若直线不过原点,一般用“原点定区域”;若直线过原点,则取点(1,0)即可.总之,尽量减少运算量.
3.画平面区域时,注意边界线的虚实问题.
