3.3.1 二元一次不等式(组)与平面区域 课件5
文档属性
| 名称 | 3.3.1 二元一次不等式(组)与平面区域 课件5 |  | |
| 格式 | zip | ||
| 文件大小 | 723.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-08 16:44:12 | ||
图片预览

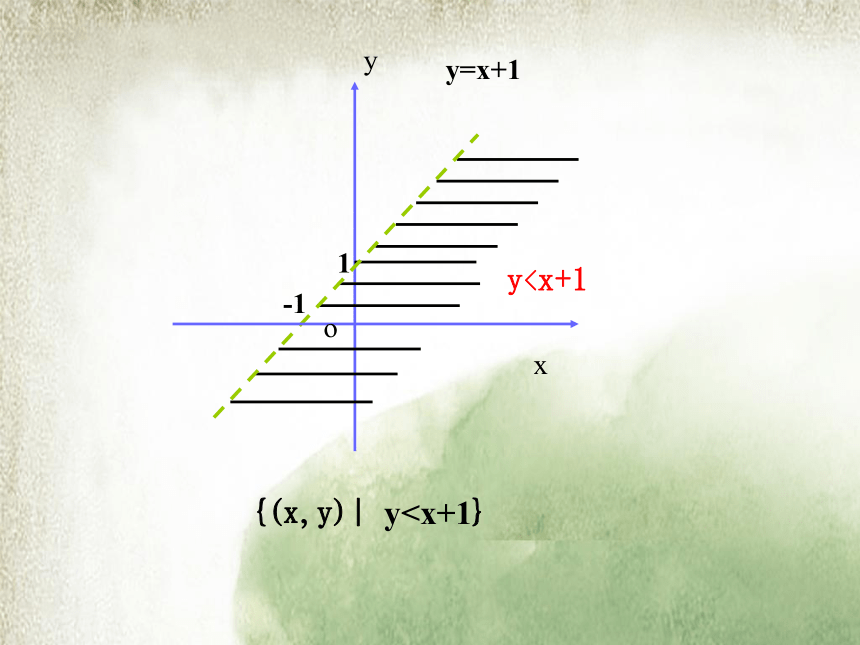


文档简介
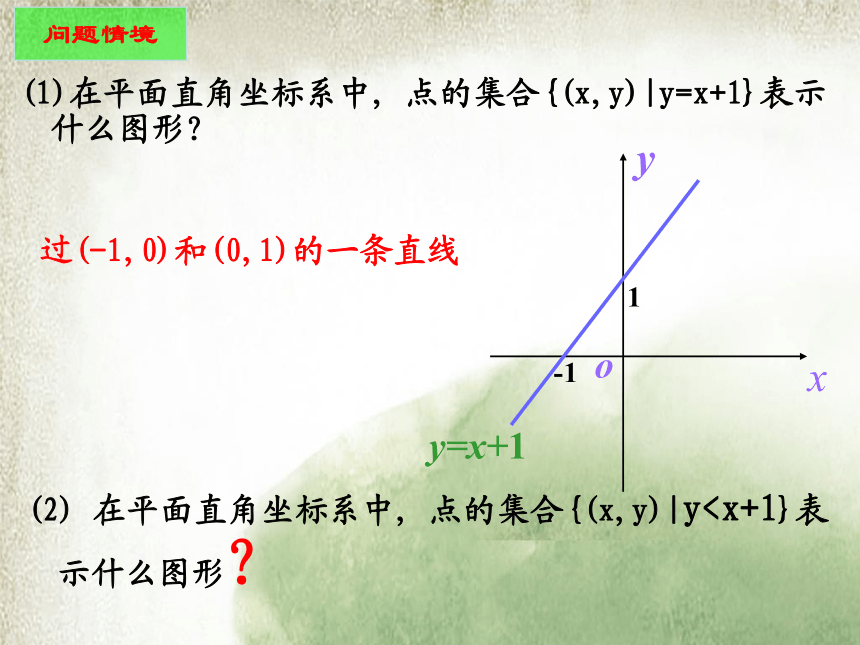
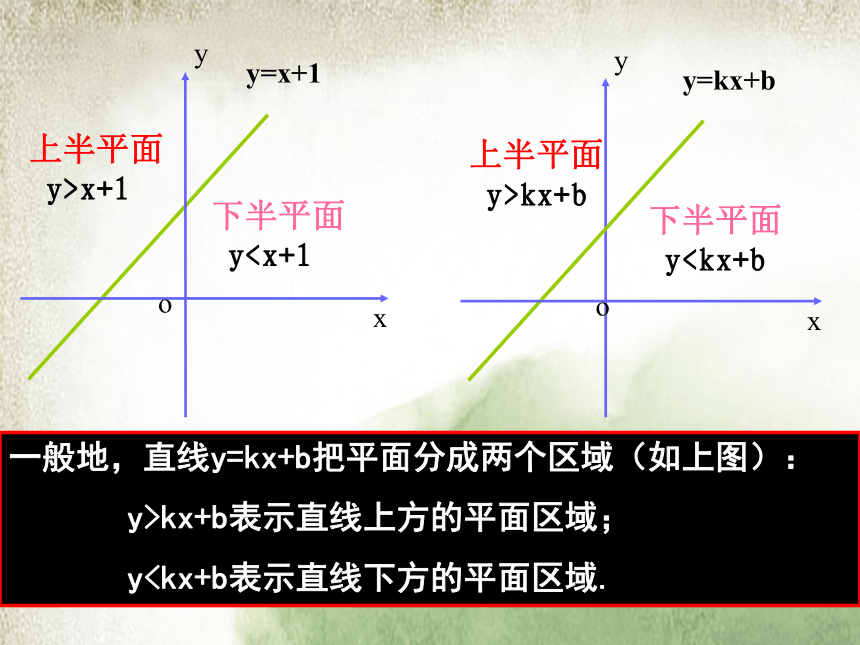
课件15张PPT。 3.3.1 二元一次不等式(组)与平面区域 (1)在平面直角坐标系中, 点的集合{(x,y)|y=x+1}表示什么图形? 问题情境过(-1,0)和(0,1)的一条直线(2) 在平面直角坐标系中, 点的集合{(x,y)|yx+1}一般地,直线y=kx+b把平面分成两个区域(如上图):
y>kx+b表示直线上方的平面区域;
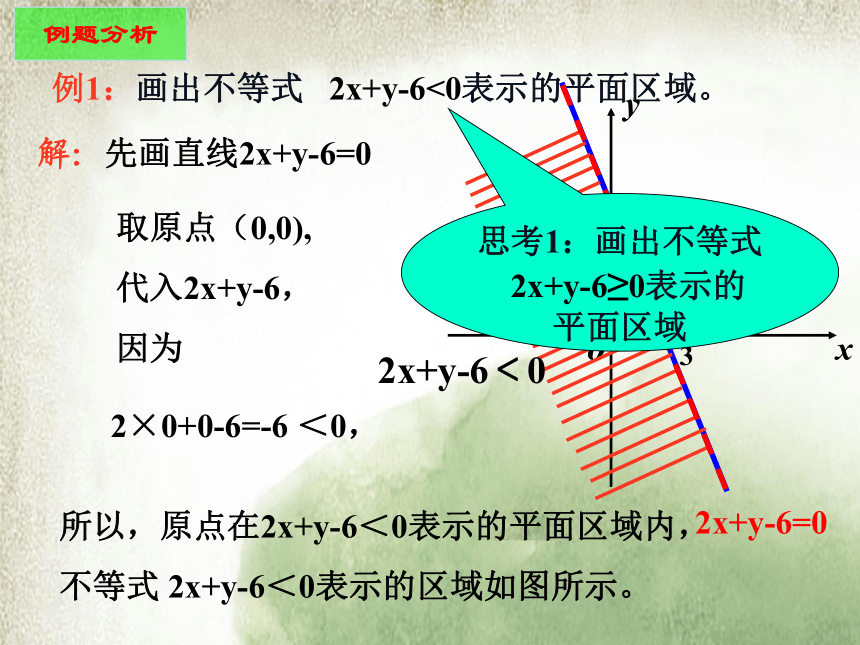
y代入2x+y-6,
因为2×0+0-6=-6 <0,所以,原点在2x+y-6<0表示的平面区域内,
不等式 2x+y-6<0表示的区域如图所示。2x+y-6=0思考1:画出不等式
2x+y-6≥0表示的
平面区域例题分析2x+y-6<0画出不等式 2x+y-6≥0表示的平面区域。注意:不等式表示的区域是否包含边界,若不包含边界,边界应画成虚线,若不便于画成虚线(如坐标轴),应通过文字加以说明。思考2:对于二元一次不等式Ax+By+C>0(A2+B2≠0)如何确定其所在的平面区域?选点法:直线定界,特殊点定域(0,0)(0,1)(1,0)练习:画出不等式 表示的平面区域。G S PG S P例题分析例3 将下列图中的平面区域(阴影部分)用不等式出来(图(1)中的区域不包含y轴)解(1) x>0(2) x+y≥0(3) 2x+y<4例题分析画出不等式组
表示的平面区域。x+y=0x=3x-y+5=0注:不等式组表示的平面区域是各不等式所表示 平面区域的公共部分。思考运用1.判断下列命题是否正确
(1)点(0,0)在平面区域x+y≥0内; ( )
(2)点(0,0)在平面区域x+y+1<0内;( )
(3)点(1,0)在平面区域y>2x内; ( )
(4)点(0,1)在平面区域x-y+1>0内.( )2.不等式x+4y-9≥0表示直线x+4y-9=0( )
A.上方的平面区域 B.上方的平面区域(包括直线)
C.下方的平面区域 D.下方的平面区域(包括直线)感受理解×B√××3. 用“上方”或“下方”填空
(1)若B>0,
不等式Ax+By+C>0表示的区域是直线Ax+By+C=0的
不等式Ax+By+C<0表示的区域是直线Ax+By+C=0的
(2)若B<0,
不等式Ax+By+C>0表示的区域是直线Ax+By+C=0的
不等式Ax+By+C<0表示的区域是直线Ax+By+C=0的
感受理解上方下方下方上方4.将下列各图中的平面区域(阴影部分)用不等式表
示出来o-11解(3) -10(2) 3x-y-3≥0感受理解(1)二元一次不等式Ax+By+C>0在平面直角坐标系
中表示什么图形?
(2)怎样画二元一次不等式(组)所表示的平面区域?
应注意哪些事项?
(3)熟记“直线定界,特殊点定域”方法。小结提高
y>kx+b表示直线上方的平面区域;
y
因为2×0+0-6=-6 <0,所以,原点在2x+y-6<0表示的平面区域内,
不等式 2x+y-6<0表示的区域如图所示。2x+y-6=0思考1:画出不等式
2x+y-6≥0表示的
平面区域例题分析2x+y-6<0画出不等式 2x+y-6≥0表示的平面区域。注意:不等式表示的区域是否包含边界,若不包含边界,边界应画成虚线,若不便于画成虚线(如坐标轴),应通过文字加以说明。思考2:对于二元一次不等式Ax+By+C>0(A2+B2≠0)如何确定其所在的平面区域?选点法:直线定界,特殊点定域(0,0)(0,1)(1,0)练习:画出不等式 表示的平面区域。G S PG S P例题分析例3 将下列图中的平面区域(阴影部分)用不等式出来(图(1)中的区域不包含y轴)解(1) x>0(2) x+y≥0(3) 2x+y<4例题分析画出不等式组
表示的平面区域。x+y=0x=3x-y+5=0注:不等式组表示的平面区域是各不等式所表示 平面区域的公共部分。思考运用1.判断下列命题是否正确
(1)点(0,0)在平面区域x+y≥0内; ( )
(2)点(0,0)在平面区域x+y+1<0内;( )
(3)点(1,0)在平面区域y>2x内; ( )
(4)点(0,1)在平面区域x-y+1>0内.( )2.不等式x+4y-9≥0表示直线x+4y-9=0( )
A.上方的平面区域 B.上方的平面区域(包括直线)
C.下方的平面区域 D.下方的平面区域(包括直线)感受理解×B√××3. 用“上方”或“下方”填空
(1)若B>0,
不等式Ax+By+C>0表示的区域是直线Ax+By+C=0的
不等式Ax+By+C<0表示的区域是直线Ax+By+C=0的
(2)若B<0,
不等式Ax+By+C>0表示的区域是直线Ax+By+C=0的
不等式Ax+By+C<0表示的区域是直线Ax+By+C=0的
感受理解上方下方下方上方4.将下列各图中的平面区域(阴影部分)用不等式表
示出来o-11解(3) -1
中表示什么图形?
(2)怎样画二元一次不等式(组)所表示的平面区域?
应注意哪些事项?
(3)熟记“直线定界,特殊点定域”方法。小结提高
