3.3.1 二元一次不等式(组)与平面区域 课件7
文档属性
| 名称 | 3.3.1 二元一次不等式(组)与平面区域 课件7 |  | |
| 格式 | zip | ||
| 文件大小 | 232.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-08 16:46:23 | ||
图片预览






文档简介
课件14张PPT。13.3.1 二元一次不等式(组)与平面区域23二元一次不等式(组) 这些满足2x+y-100<0的解对应的点与直线2x+y-100=0的位置关系怎样?几何画板4 我们把含有两个未知数,并且未知数的次数是1的不等式称为二元一次不等式. 把由几个二元一次不等式组成的不等式组称为二元一次不等式组. 满足二元一次不等式(组)的x和y的取值构成有序实数对(x,y),所有这样的有序实数对(x,y)构成的集合称为二元一次不等式(组)的解集.
有序实数对可以看成直角坐标平面内点的坐标,于是,二元一次不等式(组)的解集就可以看成直角坐标系内的点构成的集合.5二元一次方程在平面内表示什么?.
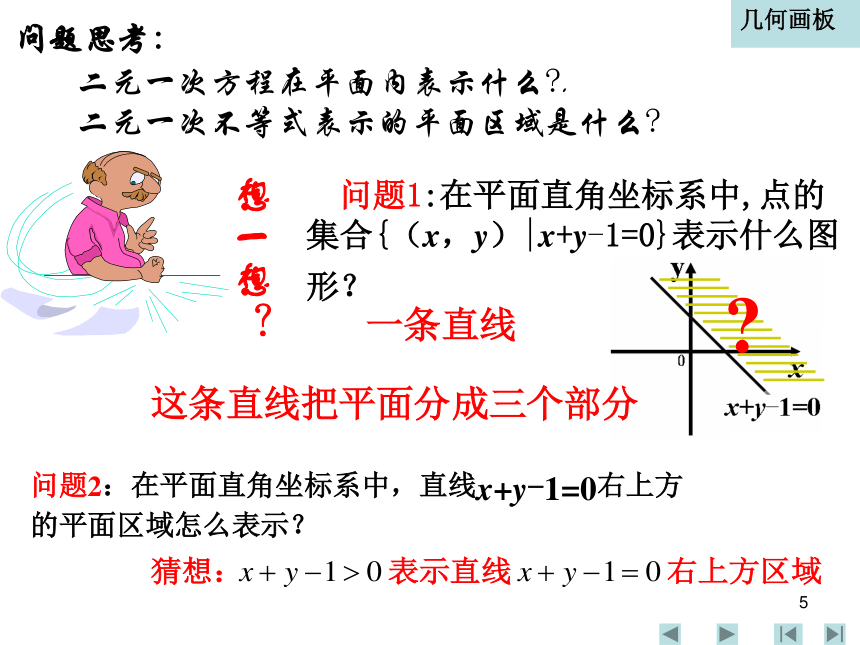
二元一次不等式表示的平面区域是什么? 问题1:在平面直角坐标系中,点的集合{(x,y)|x+y-1=0}表示什么图形? 想一想?几何画板问题2:在平面直角坐标系中,直线x+y-1=0右上方的平面区域怎么表示?6
在直线右上方任取一点(x,y),
过此点作一平行x轴的直线x>x0 , y=y0
x+y>x0+y0
x+y-1>x0+y0-1=07 直线x+y-1=0右上方的平面区域可以用点集
{(x,y)|x+y-1>0}表示 同理可知,直线x+y-1=0左下方的平面区域可以用点集{(x,y)|x+y-1<0}表示8结论:一般地,二元一次不等式Ax+By+C>0在平面直角坐标
系中表示直线Ax+By+C=0某一侧所有点组成的平面区域。
我们把直线画成虚线以表示区域不包含边界直线。(同侧同号)小结:
概括地说,判断方法为“直线定界,特殊点定域”。
特别地C≠0时,常把原点作为特殊点,即“直线定界,
原点定域”。9变式题1例1.画出不等式2x+y-6<0表示的平面区域。xyo362x+y-6=0解:先画直线2x+y-6=0
(画成虚线),取原点(0,0),代入2x+y-6,
因为2×0+0-6=-6<0,∴原点在2x+y-6<0表示的平面区域内,∴不等式2x+y-6<0表示的区域如右图所示。10变式一:画出不等式2x-3y≤6所表示的平面区域解: 2x-3y≤6即2x-3y-6 ≤0先画直线2x-3y-6 =0(画成实线)取原点(0,0),代入2x-3y-6,
因为2×0-3×0-6 =-6 ≤0,
所以,原点在2x-3y-6 ≤0表
示的平面区域内。课堂练习变式二:画出不等式x≤2所表示的平面区域.11练习1: 画出下列不等式表示的平面区域: (1)2x+3y-6>0 (2)2x+5y≥10 (3)4x-3y≤12 12答案例2:画出不等式组
表示的平面区域13解:不等式 表示直线 及其右下方的区域; 表示直线 上及其右上方的区域; 表示直线 上及其左方的区域.
所以,不等式组
表示的区域如上图所示.注:不等式组表示的平面区域是各不等式所表示平面区域的公共部分。x+y=0x=3x-y+5=014小结:
(1)二元一次方程Ax+By+C=0表示直线;
(2)二元一次不等式Ax+By+C>0表示直线Ax+By+C=0某一侧所有点组成的平面区域;
(3)Ax+By+C≥0则表示上述两部分的并集(带直线边界的半平面).
注:1.若不等式中不包含“=”,则边界应画成虚线,否则应画成实线。
2.熟记“直线定界、特殊点定域”方法的内涵。
有序实数对可以看成直角坐标平面内点的坐标,于是,二元一次不等式(组)的解集就可以看成直角坐标系内的点构成的集合.5二元一次方程在平面内表示什么?.
二元一次不等式表示的平面区域是什么? 问题1:在平面直角坐标系中,点的集合{(x,y)|x+y-1=0}表示什么图形? 想一想?几何画板问题2:在平面直角坐标系中,直线x+y-1=0右上方的平面区域怎么表示?6
在直线右上方任取一点(x,y),
过此点作一平行x轴的直线x>x0 , y=y0
x+y>x0+y0
x+y-1>x0+y0-1=07 直线x+y-1=0右上方的平面区域可以用点集
{(x,y)|x+y-1>0}表示 同理可知,直线x+y-1=0左下方的平面区域可以用点集{(x,y)|x+y-1<0}表示8结论:一般地,二元一次不等式Ax+By+C>0在平面直角坐标
系中表示直线Ax+By+C=0某一侧所有点组成的平面区域。
我们把直线画成虚线以表示区域不包含边界直线。(同侧同号)小结:
概括地说,判断方法为“直线定界,特殊点定域”。
特别地C≠0时,常把原点作为特殊点,即“直线定界,
原点定域”。9变式题1例1.画出不等式2x+y-6<0表示的平面区域。xyo362x+y-6=0解:先画直线2x+y-6=0
(画成虚线),取原点(0,0),代入2x+y-6,
因为2×0+0-6=-6<0,∴原点在2x+y-6<0表示的平面区域内,∴不等式2x+y-6<0表示的区域如右图所示。10变式一:画出不等式2x-3y≤6所表示的平面区域解: 2x-3y≤6即2x-3y-6 ≤0先画直线2x-3y-6 =0(画成实线)取原点(0,0),代入2x-3y-6,
因为2×0-3×0-6 =-6 ≤0,
所以,原点在2x-3y-6 ≤0表
示的平面区域内。课堂练习变式二:画出不等式x≤2所表示的平面区域.11练习1: 画出下列不等式表示的平面区域: (1)2x+3y-6>0 (2)2x+5y≥10 (3)4x-3y≤12 12答案例2:画出不等式组
表示的平面区域13解:不等式 表示直线 及其右下方的区域; 表示直线 上及其右上方的区域; 表示直线 上及其左方的区域.
所以,不等式组
表示的区域如上图所示.注:不等式组表示的平面区域是各不等式所表示平面区域的公共部分。x+y=0x=3x-y+5=014小结:
(1)二元一次方程Ax+By+C=0表示直线;
(2)二元一次不等式Ax+By+C>0表示直线Ax+By+C=0某一侧所有点组成的平面区域;
(3)Ax+By+C≥0则表示上述两部分的并集(带直线边界的半平面).
注:1.若不等式中不包含“=”,则边界应画成虚线,否则应画成实线。
2.熟记“直线定界、特殊点定域”方法的内涵。
