3.3.2 简单的线性规划问题 同步练习2(含答案)
文档属性
| 名称 | 3.3.2 简单的线性规划问题 同步练习2(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 76.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-08 00:00:00 | ||
图片预览



文档简介
3.3.2
简单的线性规划问题
同步练习
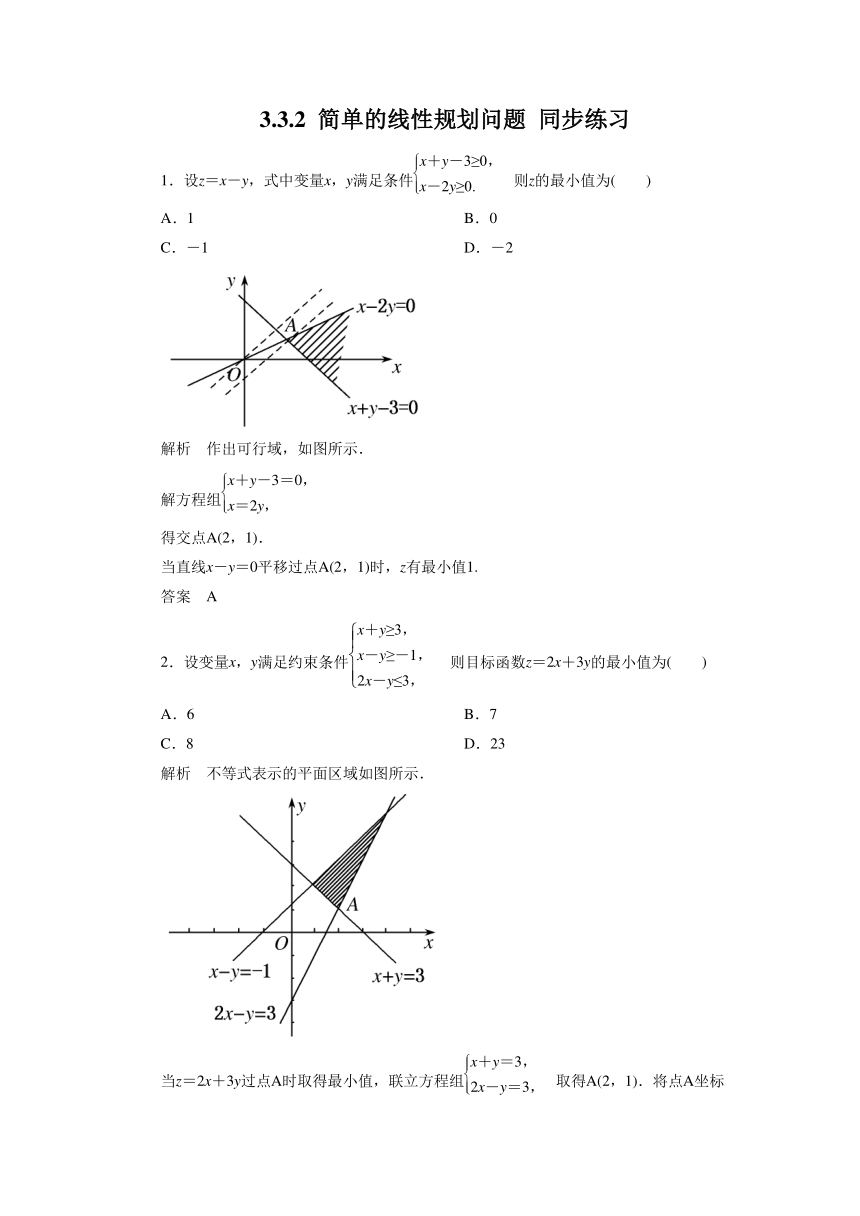
1.设z=x-y,式中变量x,y满足条件则z的最小值为( )
A.1
B.0
C.-1
D.-2
解析 作出可行域,如图所示.
解方程组
得交点A(2,1).
当直线x-y=0平移过点A(2,1)时,z有最小值1.
答案 A
2.设变量x,y满足约束条件则目标函数z=2x+3y的最小值为( )
A.6
B.7
C.8
D.23
解析 不等式表示的平面区域如图所示.
当z=2x+3y过点A时取得最小值,联立方程组取得A(2,1).将点A坐标代入z=2x+3y中得zmin=7.
答案 B
3.设x,y满足则z=x+y( )
A.有最小值2,最大值3
B.有最小值2,无最大值
C.有最大值3,无最小值
D.既无最小值,也无最大值
解析 如图,z=x+y表示直线过可行域时,在y轴上的截距,当目标函数平移至过可行域A点时,z有最小值.联立解得A(2,0).
z最小值=2,z无最大值.
答案 B
4.某企业生产甲、乙两种产品.已知生产每吨甲产品要用A原料3吨、
B原料2吨;生产每吨乙产品要用A原料1吨、B原料3吨.销售每吨甲产品可获得利润5万元、每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A原料不超过13吨、B原料不超过18吨,那么该企业可获得最大利润是( )
A.12万元
B.20万元
C.25万元
D.27万元
解析 设该企业在一个生产周期内生产甲产品x吨,乙产品y吨,获得利润z万元,则依题意,有
目标函数z=5x+3y,画出不等式组表示的平面区域及直线l0:5x+3y=0,易知当平移l0经过点(3,4)时,z取得最大值为5×3+3×4=27,故选D.
答案 D
5.某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每天的租赁费用为200元,设备乙每天的租赁费用为300元.现该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为________元.
解析 设租赁甲、乙两种设备x,y台,则
目标函数z=200x+300y,画出可行域知目标函数在点(4,5)处取得最小值,故目标函数的最小值为2300.
答案 2300
6.某厂拟用集装箱托运甲、乙两种货物,集装箱的体积、重量、可获利润和托运能力等限制数据列在下表中,那么为了获得最大利润,甲、乙两种货物应各托运的箱数为________.
货物
体积(m3/箱)
重量(50
kg/箱)
利润(百元/箱)
甲
5
2
20
乙
4
5
10
托运限制
24
13
解析 设甲、乙两种货物应各托运的箱数为x,y,则
目标函数z=20x+10y,画出可行域如图.
由得A(4,1).
易知当直线2x+y=0平移经过点A时,z取得最大值.
答案 4,1
7.某工厂制造A种仪器45台,B种仪器55台,现需用薄钢板给每台仪器配一个外壳.已知钢板有甲、乙两种规格:甲种钢板每张面积2
m2,每张可作A种仪器外壳3个和B种仪器外壳5个,乙种钢板每张面积3
m2,每张可作A种仪器外壳6个和B种仪器外壳6个,问甲、乙两种钢板各用多少张才能用料最省?(“用料最省”是指所用钢板的总面积最小)
解 设用甲种钢板x张,乙种钢板y张,依题意
钢板总面积z=2x+3y.作出可行域,如图所示.
由图可知当直线z=2x+3y过点P时,z最小.
由方程组得
所以甲、乙两种钢板各用5张用料最省.
8.某运输公司接受了向抗洪救灾地区每天送至少180
t支援物资的任务.该公司有8辆载重6
t的A型卡车与4辆载重为10
t的B型卡车,有10名驾驶员,每辆卡车每天往返的次数为A型卡车4次,B型卡车3次;每辆卡车每天往返的成本费A型为320元,B型为504元.请为公司安排一下,应如何调配车辆,才能使公司所花的成本费最低?若只安排A型或B型卡车,所花的成本费分别是多少?
解 设需A型、B型卡车分别为x辆和y辆.列表分析数据.
A型车
B型车
限量
车辆数
x
y
10
运物吨数
24x
30y
180
费用
320x
504y
z
由表可知x,y满足的线性条件
且z=320x+504y.
作出线性区域,如图所示.可知当直线z=320x+504y过A(7.5,0)时,z最小,但A(7.5,0)不是整点,继续向上平移直线z=320x+504y,可知点(5,2)是最优解.这时zmin=320×5+504×2=2608(元),即用5辆A型车,2辆B型车,成本费最低.
若只用A型车,成本费为8×320=2560(元),
只用B型车,成本费为×504=3024(元).
9.某公司有60万元资金,计划投资甲、乙两个项目,按要求对项目甲的投资不小于对项目乙的投资的,且对每个项目的投资不能低于5万元,对项目甲每投资1万元可获得0.4万元的利润,对项目乙每投资1万元可获得0.6万元的利润,问该公司正式投资后,在两个项目上共可获得的最大利润为多少?
解 设投资甲项目x万元,投资乙项目y万元,共可获利z万元,则z=0.4x+0.6y.
由题意知
作出可行域如图,
由图可以看出,当直线经过可行域上的点A(24,36)时,z取得最大值.
z=0.4x+0.6y=0.4×24+0.6×36=31.2.
即该公司正式投资后,在两个项目上共可获得的最大利润为31.2万元.
简单的线性规划问题
同步练习
1.设z=x-y,式中变量x,y满足条件则z的最小值为( )
A.1
B.0
C.-1
D.-2
解析 作出可行域,如图所示.
解方程组
得交点A(2,1).
当直线x-y=0平移过点A(2,1)时,z有最小值1.
答案 A
2.设变量x,y满足约束条件则目标函数z=2x+3y的最小值为( )
A.6
B.7
C.8
D.23
解析 不等式表示的平面区域如图所示.
当z=2x+3y过点A时取得最小值,联立方程组取得A(2,1).将点A坐标代入z=2x+3y中得zmin=7.
答案 B
3.设x,y满足则z=x+y( )
A.有最小值2,最大值3
B.有最小值2,无最大值
C.有最大值3,无最小值
D.既无最小值,也无最大值
解析 如图,z=x+y表示直线过可行域时,在y轴上的截距,当目标函数平移至过可行域A点时,z有最小值.联立解得A(2,0).
z最小值=2,z无最大值.
答案 B
4.某企业生产甲、乙两种产品.已知生产每吨甲产品要用A原料3吨、
B原料2吨;生产每吨乙产品要用A原料1吨、B原料3吨.销售每吨甲产品可获得利润5万元、每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A原料不超过13吨、B原料不超过18吨,那么该企业可获得最大利润是( )
A.12万元
B.20万元
C.25万元
D.27万元
解析 设该企业在一个生产周期内生产甲产品x吨,乙产品y吨,获得利润z万元,则依题意,有
目标函数z=5x+3y,画出不等式组表示的平面区域及直线l0:5x+3y=0,易知当平移l0经过点(3,4)时,z取得最大值为5×3+3×4=27,故选D.
答案 D
5.某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每天的租赁费用为200元,设备乙每天的租赁费用为300元.现该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为________元.
解析 设租赁甲、乙两种设备x,y台,则
目标函数z=200x+300y,画出可行域知目标函数在点(4,5)处取得最小值,故目标函数的最小值为2300.
答案 2300
6.某厂拟用集装箱托运甲、乙两种货物,集装箱的体积、重量、可获利润和托运能力等限制数据列在下表中,那么为了获得最大利润,甲、乙两种货物应各托运的箱数为________.
货物
体积(m3/箱)
重量(50
kg/箱)
利润(百元/箱)
甲
5
2
20
乙
4
5
10
托运限制
24
13
解析 设甲、乙两种货物应各托运的箱数为x,y,则
目标函数z=20x+10y,画出可行域如图.
由得A(4,1).
易知当直线2x+y=0平移经过点A时,z取得最大值.
答案 4,1
7.某工厂制造A种仪器45台,B种仪器55台,现需用薄钢板给每台仪器配一个外壳.已知钢板有甲、乙两种规格:甲种钢板每张面积2
m2,每张可作A种仪器外壳3个和B种仪器外壳5个,乙种钢板每张面积3
m2,每张可作A种仪器外壳6个和B种仪器外壳6个,问甲、乙两种钢板各用多少张才能用料最省?(“用料最省”是指所用钢板的总面积最小)
解 设用甲种钢板x张,乙种钢板y张,依题意
钢板总面积z=2x+3y.作出可行域,如图所示.
由图可知当直线z=2x+3y过点P时,z最小.
由方程组得
所以甲、乙两种钢板各用5张用料最省.
8.某运输公司接受了向抗洪救灾地区每天送至少180
t支援物资的任务.该公司有8辆载重6
t的A型卡车与4辆载重为10
t的B型卡车,有10名驾驶员,每辆卡车每天往返的次数为A型卡车4次,B型卡车3次;每辆卡车每天往返的成本费A型为320元,B型为504元.请为公司安排一下,应如何调配车辆,才能使公司所花的成本费最低?若只安排A型或B型卡车,所花的成本费分别是多少?
解 设需A型、B型卡车分别为x辆和y辆.列表分析数据.
A型车
B型车
限量
车辆数
x
y
10
运物吨数
24x
30y
180
费用
320x
504y
z
由表可知x,y满足的线性条件
且z=320x+504y.
作出线性区域,如图所示.可知当直线z=320x+504y过A(7.5,0)时,z最小,但A(7.5,0)不是整点,继续向上平移直线z=320x+504y,可知点(5,2)是最优解.这时zmin=320×5+504×2=2608(元),即用5辆A型车,2辆B型车,成本费最低.
若只用A型车,成本费为8×320=2560(元),
只用B型车,成本费为×504=3024(元).
9.某公司有60万元资金,计划投资甲、乙两个项目,按要求对项目甲的投资不小于对项目乙的投资的,且对每个项目的投资不能低于5万元,对项目甲每投资1万元可获得0.4万元的利润,对项目乙每投资1万元可获得0.6万元的利润,问该公司正式投资后,在两个项目上共可获得的最大利润为多少?
解 设投资甲项目x万元,投资乙项目y万元,共可获利z万元,则z=0.4x+0.6y.
由题意知
作出可行域如图,
由图可以看出,当直线经过可行域上的点A(24,36)时,z取得最大值.
z=0.4x+0.6y=0.4×24+0.6×36=31.2.
即该公司正式投资后,在两个项目上共可获得的最大利润为31.2万元.
