八年级第十三章全等三角形 单元测试试题
文档属性
| 名称 | 八年级第十三章全等三角形 单元测试试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 414.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-09 00:00:00 | ||
图片预览


文档简介
八年级数学单元试题《全等三角形》
一、选择题:(每小题3分,共36分)
1、根据下列条件画三角形,不能唯一确定三角形的是( ).
A、已知三个角 B、已知三边 C、已知两角和一边 D、已知两边和夹角
2、下列语句不是命题的是( )
A、对顶角相等 B、连接AB并延长至C点 C、内错角相等 D、同角的余角相等
3、如图,已知MB=ND,∠MBA=∠NDC,不能判定△ABM≌△CDN的条件是( )
A、∠M=∠N B、AB=CD C、AM=CN D、AM∥CN
4、某同学把一块三角形的玻璃打碎也成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )A、带①去 B、带②去C、带③去 D、带①和②去
第3题 第4题
5、如图19-1,要用“SAS”证明△ABC≌△ADE,已知AB=AD,AC=AE,则还需条件( )
A、∠B=∠D B、∠C=∠E C、∠1 =∠2 D、∠3= ∠4
6、△ABC中,AB=AC,BD、CE是AC、AB边上的高,则BE与CD的大小关系为( )
A、BE>CD B、BE=CD C、BE<CD D、不确定
7、如图19-2,已知:∠ACB=90°,BC=AC,AC=AE,DE⊥AB于E.则下列结论正确的是( )
①△AED≌△ACD;②EB=DC;③点D在∠BAC的平分线上.
A、只有① B、只有② C、只有①② D、①②③
8、下列命题是假命题的有 ( )
①若a2=b2,则a=b;②一个角的余角大于这个角;③若a,b是有理数,则;④如果∠A=∠B,那∠A与∠B是对顶角.21世纪教育网版权所有
A、1个 B、2个 C、3个 D、4个
9、已知:∠AOB,求作射线OC,使OC平分∠AOB,作图的合理顺序是( )
①作射线OC;②在OA和OB上,分别截取OD、OE,使OD=OE;③分别以D、E为圆心,大于DE为半径作弧,在∠AOB内两弧交于点G 21教育网
A、①②③ B、②①③ C、②③① D、③②①
10、如果D是△ABC中BC边上一点,且△ADB≌△ADC,
则△ABC是 ( )
A、锐角三角形 B、钝角三角形 C、等腰三角形 D、直角三角形
11、用尺规作已知角平分线,其根据是构造两个三角形全等,它所用到的识别方法是( ) A、SAS B、ASA C、AAS D、SSS21cnjy.com
12、如图,∠1=∠2,BC=EF,欲证△ABC≌△DEF,则须补充一个条件是( )
A、AB=DE B、∠ACE=∠DFB C、BF=EC D、∠ABC=∠DEF
二、填空题(每小题3分,共24分)
13、命题“等腰三角形的两底角相等”的逆命题是
14、已知:如图,△ABE≌△ACD,∠B=∠C,则∠AEB=_______,AE=________.
15、如图,AC=AD,BC=BD,AB与CD相交于O.则AB与CD的关系是
16、如图,AB=CD,AD、BC相交于O,要使ΔABOΔDCO,应添加的条件是 .
第14题 第15题 第16题
17、如图,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于P点,
PE=3cm,则P点到直线AB的距离是_____________
18、如图,AD⊥BC,DE⊥AB,DF⊥AC,D、E、F是垂足,BD=CD,
那么图中的全等三角形有
19、在ΔABC中,AD是边BC上的中线,已知:AB=5,AC=3,则中线
AD的取值范围是
20、如图3,在等腰Rt△ABC中,∠C=90°,AC=BC,AD平分
∠BAC交BC于D,DE⊥AB于D,若AB=10,则
△BDE的周长等于
三、作图题:(利用尺规作图,不写作法,但要保留作图痕迹)(每小题6分,共12分)
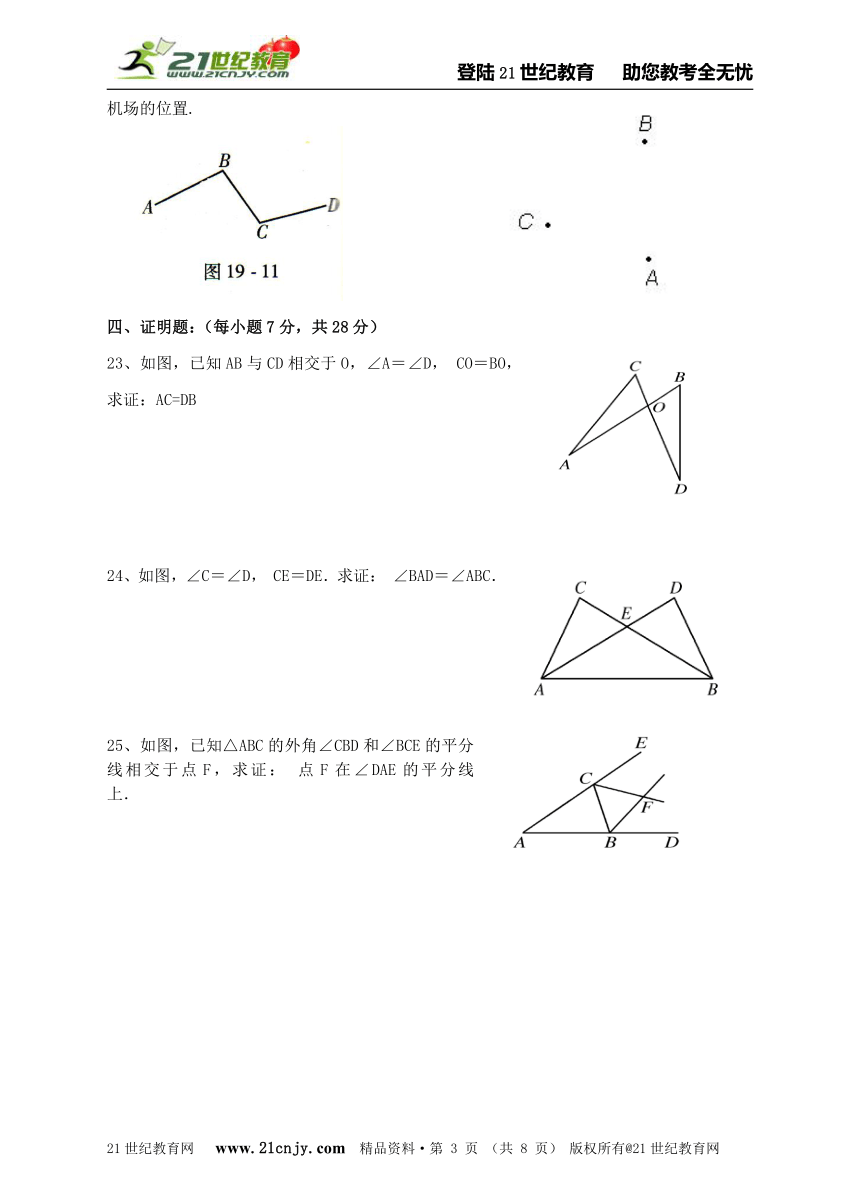
21、如图19-11,作出AB的中点M,作出∠BCD的平分线CN.
22、“太湖明珠”无锡要建特大城市,有人建议无锡()、江阴()、宜兴()三市共建一个国际机场,使飞机场到江阴、宜兴两城市距离相等,且到无锡市的距离最近.请你设计机场的位置.www.21-cn-jy.com
四、证明题:(每小题7分,共28分)
23、如图,已知AB与CD相交于O,∠A=∠D, CO=BO,求证:AC=DB
24、如图,∠C=∠D, CE=DE.求证: ∠BAD=∠ABC.
25、如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,求证: 点F在∠DAE的平分线上.2·1·c·n·j·y
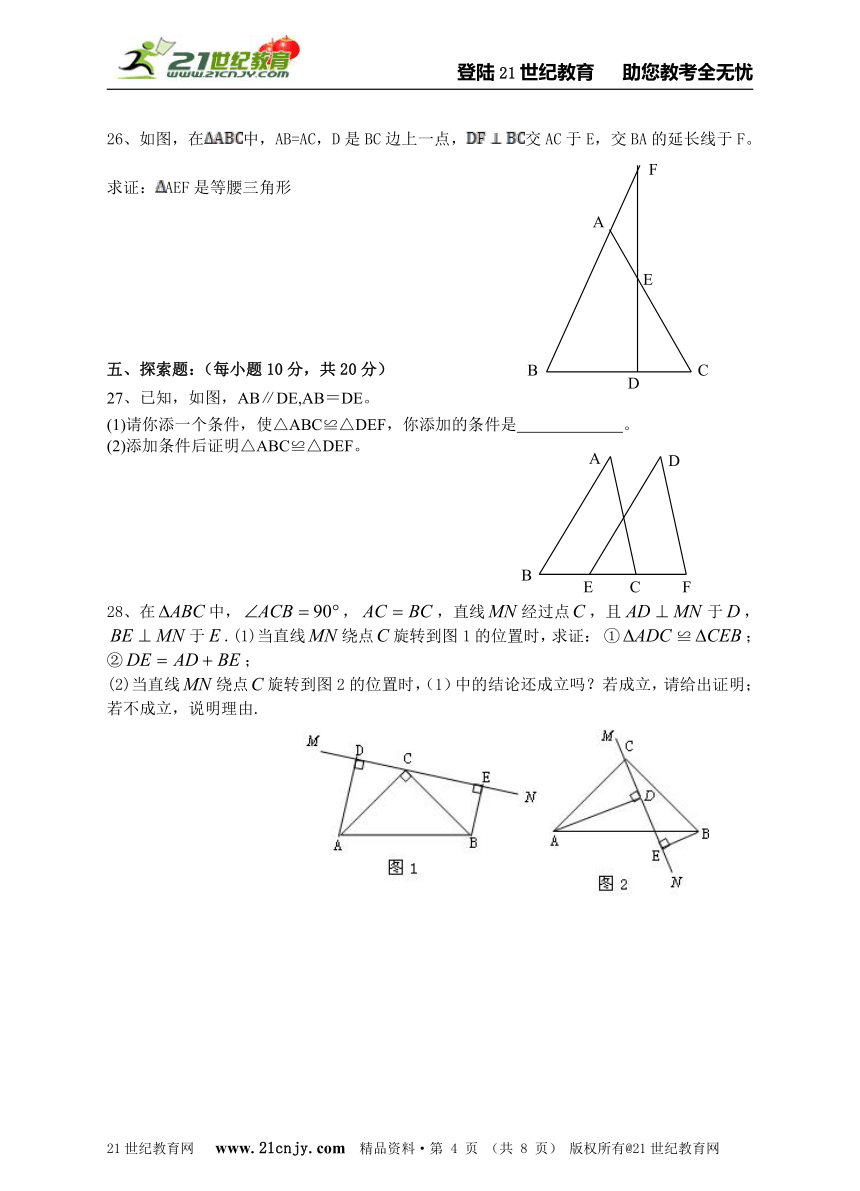
26、如图,在中,AB=AC,D是BC边上一点,交AC于E,交BA的延长线于F。求证:AEF是等腰三角形21·cn·jy·com
五、探索题:(每小题10分,共20分)
27、已知,如图,AB∥DE,AB=DE。
(1)请你添一个条件,使△ABC≌△DEF,你添加的条件是 。
(2)添加条件后证明△ABC≌△DEF。
28、在中,,,直线经过点,且于,于.(1)当直线绕点旋转到图1的位置时,求证: ①≌;②;【来源:21·世纪·教育·网】
(2)当直线绕点旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由. www-2-1-cnjy-com
八年级数学单元试题《全等三角形》参考答案
一、选择题:
1、A(解析:考虑全等三角形的判定方法,AAA,SSA不能判定三角形全等,故选A)
2、B(解析:表示判断的语句叫做命题,只有B不表示判断,故选B)
3、C(解析:SAS、ASA、AAS、SSS四种判定方法都考虑,一一排除,故选C)
4、C(解析:ASA)
5、C(解析:由得,用SAS证明全等)
6、B(解析:利用等底等高的三角形的面积相等)
7、D(解析:利用HL证全等和等腰三角形的判定,三个结论都是正确的,故选D)
8、D(解析:考查真假命题,四个命题都是假命题,故选D)
9、C(解析:考查尺规作图的基本步骤)
10、C(解析:利用全等可得两边相等,再利用等腰三角形的定义)
11、D(解析:基本作图的理论依据是SSS)
12、D(解析:考查学生对全等三角形判定是否熟练,能否灵活运用)
二、填空题:
13、两个角相等的三角形是等腰三角形(解析:写逆命题不是把条件和结论交换,要改变个别的字词句)
14、(解析:全等三角形的对应边、角相等,对应的点写在对应的位置上)
15、AB垂直平分CD(解析:利用SSS全等和三线合一)
20、10cm(解析:证得AC=AE,CD=ED,得AB=AE+EB=AC+BE=BC+BE=CD+BD+BE=DE+BD+BE=BDE的周长)21·世纪*教育网
三、作图题:(图略)
21、作线段AB的垂直平分线与AB的交点就是M,作角平分线
22、作线段BC的垂直平分线n,再过点A作n的垂线与n的交点就是机场的位置
四、23、解析:图中有隐藏条件对顶角相等即,利用AAS可证得AC=DB
证明:在中
24、解析:图中有隐藏条件对顶角相等即,利用ASA可证得AE=BE得
证明:在中
25、解析:作辅助线:过F作,可用角平分线的性质定理和逆定理。
证明:过F作
)
点F在∠DAE的平分线上(到一个角两边距离相等的点在这个角的平分线上)
26、解析:本题可用直角三角形的两锐角互余,等腰三角形的性质和判定解决。
证明:
(直角三角形的两锐角互余)
27、解析:(1)或或AB//DF
(2)若①,就用ASA;
②,就用SAS;
③或AB//DF就用AAS。证明略
28、解析:几何变式题(1)(2)的证明思路一样,书写证明过程的个别细节不同。
(1)证明:
在中
(2)在(1)中的结论仍然成立。
在中
一、选择题:(每小题3分,共36分)
1、根据下列条件画三角形,不能唯一确定三角形的是( ).
A、已知三个角 B、已知三边 C、已知两角和一边 D、已知两边和夹角
2、下列语句不是命题的是( )
A、对顶角相等 B、连接AB并延长至C点 C、内错角相等 D、同角的余角相等
3、如图,已知MB=ND,∠MBA=∠NDC,不能判定△ABM≌△CDN的条件是( )
A、∠M=∠N B、AB=CD C、AM=CN D、AM∥CN
4、某同学把一块三角形的玻璃打碎也成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )A、带①去 B、带②去C、带③去 D、带①和②去
第3题 第4题
5、如图19-1,要用“SAS”证明△ABC≌△ADE,已知AB=AD,AC=AE,则还需条件( )
A、∠B=∠D B、∠C=∠E C、∠1 =∠2 D、∠3= ∠4
6、△ABC中,AB=AC,BD、CE是AC、AB边上的高,则BE与CD的大小关系为( )
A、BE>CD B、BE=CD C、BE<CD D、不确定
7、如图19-2,已知:∠ACB=90°,BC=AC,AC=AE,DE⊥AB于E.则下列结论正确的是( )
①△AED≌△ACD;②EB=DC;③点D在∠BAC的平分线上.
A、只有① B、只有② C、只有①② D、①②③
8、下列命题是假命题的有 ( )
①若a2=b2,则a=b;②一个角的余角大于这个角;③若a,b是有理数,则;④如果∠A=∠B,那∠A与∠B是对顶角.21世纪教育网版权所有
A、1个 B、2个 C、3个 D、4个
9、已知:∠AOB,求作射线OC,使OC平分∠AOB,作图的合理顺序是( )
①作射线OC;②在OA和OB上,分别截取OD、OE,使OD=OE;③分别以D、E为圆心,大于DE为半径作弧,在∠AOB内两弧交于点G 21教育网
A、①②③ B、②①③ C、②③① D、③②①
10、如果D是△ABC中BC边上一点,且△ADB≌△ADC,
则△ABC是 ( )
A、锐角三角形 B、钝角三角形 C、等腰三角形 D、直角三角形
11、用尺规作已知角平分线,其根据是构造两个三角形全等,它所用到的识别方法是( ) A、SAS B、ASA C、AAS D、SSS21cnjy.com
12、如图,∠1=∠2,BC=EF,欲证△ABC≌△DEF,则须补充一个条件是( )
A、AB=DE B、∠ACE=∠DFB C、BF=EC D、∠ABC=∠DEF
二、填空题(每小题3分,共24分)
13、命题“等腰三角形的两底角相等”的逆命题是
14、已知:如图,△ABE≌△ACD,∠B=∠C,则∠AEB=_______,AE=________.
15、如图,AC=AD,BC=BD,AB与CD相交于O.则AB与CD的关系是
16、如图,AB=CD,AD、BC相交于O,要使ΔABOΔDCO,应添加的条件是 .
第14题 第15题 第16题
17、如图,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于P点,
PE=3cm,则P点到直线AB的距离是_____________
18、如图,AD⊥BC,DE⊥AB,DF⊥AC,D、E、F是垂足,BD=CD,
那么图中的全等三角形有
19、在ΔABC中,AD是边BC上的中线,已知:AB=5,AC=3,则中线
AD的取值范围是
20、如图3,在等腰Rt△ABC中,∠C=90°,AC=BC,AD平分
∠BAC交BC于D,DE⊥AB于D,若AB=10,则
△BDE的周长等于
三、作图题:(利用尺规作图,不写作法,但要保留作图痕迹)(每小题6分,共12分)
21、如图19-11,作出AB的中点M,作出∠BCD的平分线CN.
22、“太湖明珠”无锡要建特大城市,有人建议无锡()、江阴()、宜兴()三市共建一个国际机场,使飞机场到江阴、宜兴两城市距离相等,且到无锡市的距离最近.请你设计机场的位置.www.21-cn-jy.com
四、证明题:(每小题7分,共28分)
23、如图,已知AB与CD相交于O,∠A=∠D, CO=BO,求证:AC=DB
24、如图,∠C=∠D, CE=DE.求证: ∠BAD=∠ABC.
25、如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,求证: 点F在∠DAE的平分线上.2·1·c·n·j·y
26、如图,在中,AB=AC,D是BC边上一点,交AC于E,交BA的延长线于F。求证:AEF是等腰三角形21·cn·jy·com
五、探索题:(每小题10分,共20分)
27、已知,如图,AB∥DE,AB=DE。
(1)请你添一个条件,使△ABC≌△DEF,你添加的条件是 。
(2)添加条件后证明△ABC≌△DEF。
28、在中,,,直线经过点,且于,于.(1)当直线绕点旋转到图1的位置时,求证: ①≌;②;【来源:21·世纪·教育·网】
(2)当直线绕点旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由. www-2-1-cnjy-com
八年级数学单元试题《全等三角形》参考答案
一、选择题:
1、A(解析:考虑全等三角形的判定方法,AAA,SSA不能判定三角形全等,故选A)
2、B(解析:表示判断的语句叫做命题,只有B不表示判断,故选B)
3、C(解析:SAS、ASA、AAS、SSS四种判定方法都考虑,一一排除,故选C)
4、C(解析:ASA)
5、C(解析:由得,用SAS证明全等)
6、B(解析:利用等底等高的三角形的面积相等)
7、D(解析:利用HL证全等和等腰三角形的判定,三个结论都是正确的,故选D)
8、D(解析:考查真假命题,四个命题都是假命题,故选D)
9、C(解析:考查尺规作图的基本步骤)
10、C(解析:利用全等可得两边相等,再利用等腰三角形的定义)
11、D(解析:基本作图的理论依据是SSS)
12、D(解析:考查学生对全等三角形判定是否熟练,能否灵活运用)
二、填空题:
13、两个角相等的三角形是等腰三角形(解析:写逆命题不是把条件和结论交换,要改变个别的字词句)
14、(解析:全等三角形的对应边、角相等,对应的点写在对应的位置上)
15、AB垂直平分CD(解析:利用SSS全等和三线合一)
20、10cm(解析:证得AC=AE,CD=ED,得AB=AE+EB=AC+BE=BC+BE=CD+BD+BE=DE+BD+BE=BDE的周长)21·世纪*教育网
三、作图题:(图略)
21、作线段AB的垂直平分线与AB的交点就是M,作角平分线
22、作线段BC的垂直平分线n,再过点A作n的垂线与n的交点就是机场的位置
四、23、解析:图中有隐藏条件对顶角相等即,利用AAS可证得AC=DB
证明:在中
24、解析:图中有隐藏条件对顶角相等即,利用ASA可证得AE=BE得
证明:在中
25、解析:作辅助线:过F作,可用角平分线的性质定理和逆定理。
证明:过F作
)
点F在∠DAE的平分线上(到一个角两边距离相等的点在这个角的平分线上)
26、解析:本题可用直角三角形的两锐角互余,等腰三角形的性质和判定解决。
证明:
(直角三角形的两锐角互余)
27、解析:(1)或或AB//DF
(2)若①,就用ASA;
②,就用SAS;
③或AB//DF就用AAS。证明略
28、解析:几何变式题(1)(2)的证明思路一样,书写证明过程的个别细节不同。
(1)证明:
在中
(2)在(1)中的结论仍然成立。
在中
