太原市数学中考第十五章三角形与多边形知识点聚焦
文档属性
| 名称 | 太原市数学中考第十五章三角形与多边形知识点聚焦 | 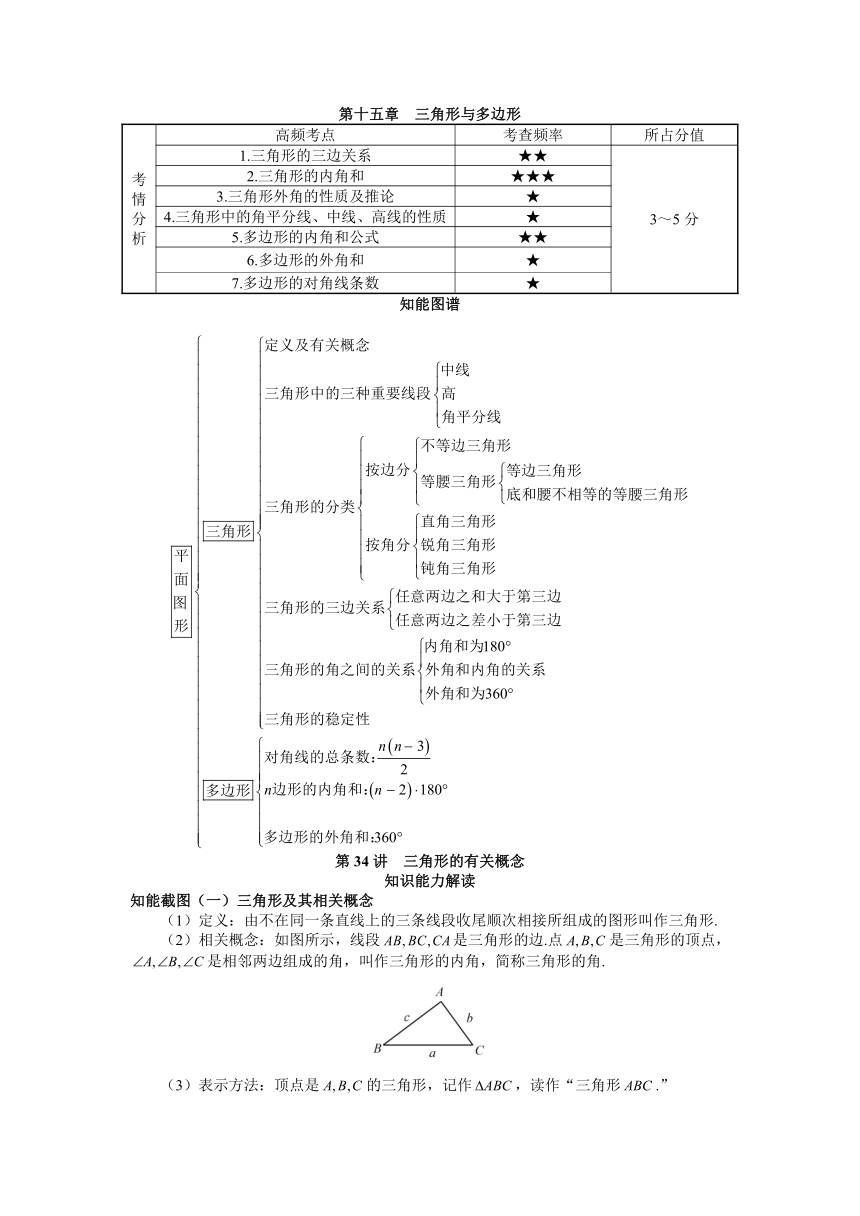 | |
| 格式 | zip | ||
| 文件大小 | 68.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-08 20:59:33 | ||
图片预览


文档简介
第十五章
三角形与多边形
考情分析
高频考点
考查频率
所占分值
1.三角形的三边关系
★★
3~5分
2.三角形的内角和
★★★
3.三角形外角的性质及推论
★
4.三角形中的角平分线、中线、高线的性质
★
5.多边形的内角和公式
★★
6.多边形的外角和
★
7.多边形的对角线条数
★
知能图谱
第34讲
三角形的有关概念
知识能力解读
知能截图(一)三角形及其相关概念
(1)定义:由不在同一条直线上的三条线段收尾顺次相接所组成的图形叫作三角形.
(2)相关概念:如图所示,线段是三角形的边.点是三角形的顶点,是相邻两边组成的角,叫作三角形的内角,简称三角形的角.
(3)表示方法:顶点是的三角形,记作,读作“三角形.”
(4)三角形的外角:三角形的一边与另一边的延长线组成的角,叫作三角形的外角.
知能解读(二)三角形的分类
(1)按角分:
(
三角形
)(2)按边分:
注意
不能把等边三角形算作是单独的一类,等腰三角形包括等边三角形,等边三角形是特殊的等腰三角形,即底边和腰相等的等腰三角形.
知能解读(三)三角形中的重要线段
1三角形的角平分线
三角形的一个角的平分线与这个角的对边相交,顶点和交点之间的线段叫作三角形的角平分线.
2三角形的中线
在三角形中,连接一个顶点和它的对边中点的线段叫作三角形的中线.
三角形的三条中线相交于一点,三角形三条中线的交点,叫作三角形的重心.
3三角形的高
从三角形的一个顶点向它的对边所在直线画垂线,顶点和垂足间的线段叫作三角形的高.
注意
(1)三角形中,角平分线、中线以及高都有三条,且分别都交于一点.
(2)这三种线都是线段.
(3)一个三角形中,①三条角平分线都在三角形内;②三条中线也都在三角形内;③三条高的位置:a.锐角三角形的三条高都在三角形内;b.直角三角形有两条高为直角边,斜边上的高在三角形内;c.钝角三角形有一条高在三角形内,另两条高在三角形外.
知能解读(四)三角形的三边关系
(1)三角形的和大于等三边,(2)三角形两边的差小于第三边.
注意
根据三角形的三边关系,只要比较两条线段的长度和大于最长线段的长度即可构成三角形.
知能解读(五)三角形的稳定性
如果三角形的三条边固定,那么三角形的形状和大小就完全确定了,三角形的这个特征叫作三角形的稳定性.除了三角形外,其他多边形不具备稳定性,因此在生产建设中,为达到稳固的目的,把一些部件都做成三角形结构.
知能解读(六)三角形中有关角的结论
(1)三角形内角和定理:三角形三个内角和等于.
(2)三角形的外角等于与它不相邻的两个内角的和.
(3)三角形的一个外角大于任何一个和它不相邻的内角.
(4)直角三角形的两个锐角互余;有两个角互余的三角形是直角三角形.
方法技巧归纳
方法技巧(一)利用三角形中角的关系求值与证明
三角形中求角的读数,涉及的知识点有三个:(1)三角形的内角和;(2)三角形的外角性质;(3)三角形的内角与相邻外角互补.
点拨
充分利用角平分线的性质和三角形的内外交的关系建立与的练习是解决问题的关键.
方法技巧(二)利用三角形三边关系判断是否能构成三角形
按照三角形三边关系去判断时必须满足任意两边之和大于第三边,而在实际使用时,只要其中较小的两条线段长度的和能够大于第三条线段的长度,就能构成三角形.
点拨
三条线段能否组成三角形,可用如下方法来进行判定:设三条线段的长为,并满足,若,则线段可以组成三角形.
方法技巧(三)利用三角形的三边关系确定第三边的取值范围
根据三角形两边和大于第三边,两边的差小于第三边,可得第三边应小于两边的和,并且大于两边的差.
点拨
已知三角形的两边长,可根据三边关系确定第三边的取值范围;另两边之差的绝对值<第三边<另两边之和.
方法技巧(四)利用三角形中线的概念证明面积相等
三角形的一条中线把原三角形分成两个三角形,根据垂线的性质可得到这两个三角形等底同高,因此其面积相等,利用这一特点可以证明有关的面积关系问题.
点拨
三角形的中线把它分成两个面积相等的三角形.
方法技巧(五)利用三角形的稳定性解决实际问题
把实际问题转化为三角形问题,用三角形的稳定性未解释.
方法技巧(六)三角形内角和的应用技巧
点拨
当要求的角度列式计算很复杂时,可以通过列方程求解,体现方程思想.
易混易错辨析
易混易错知识
1.角平分线和三角形的角平分线.
区别:角平分线是一条射线,而三角形的角平分线是一条线段.
2.三角形的角平分线、中线和高.
区别:三角形的角平分线是一个角的平分线和对边相交所构成的线段,而高是过一个顶点向对边所在直线作的垂线段.
易混易错(一)忽视三角形“三边关系”致错
易混易错(二)不能准确画出钝角三角形的三条高
中考试题研究
中考命题规律
三角形是历年中考的必考内容,考查热点是运用三角形的三边关系,内角和以及内外交之间的关系进行有关推力与计算,多以填空题、选择题的形式出现.
中考试题(一)三角形内角和的应用
中考试题(二)三角形中角的运算求解
中考试题(三)三角形三边关系的应用
第35讲
多边形的内角和与外角和
知识能力解读
知能解读(一)多边形的有关概念
1多边形的定义
在平面内,由一些线段首尾顺次相接组成的封闭图形叫作多边形.
注意
多边形根据边数的不同可分为三角形、四边形、五边形、…,我们所学的多边形都是凸多边形(整个图形都在任一边所在直线同旁的多边形),即组成多边形的每一个内角都大于,且小于.
2正多边形
各个角都相等,各条边都相等的多边形叫作正多边形,比如:等边三角形、正方形等.
3相关概念
(1)内角:多边形相邻两边组成的角叫作它的内角.
(2)外角:多边形的一边与它的邻边的延长线组成的角叫作多边形的外角.
(3)对角线:连接多边形不相邻的两个顶点的线段,叫作多边形的对角线.
注意
(1)一个边形从一个顶点出发有条对角线,所有对角线的条数是.
(2)把多边形转化成三角形求解的常用方法是连接对角线.
知能解读(二)多边形的内角和公式:边形的内角和等于
知能解读(三)多边形的外角和等于
注意
(1)多边形的外角和不随边数的变化而变化,但内角和随边数的变化而变化,且边数每增加1,内角和就增加;(2)多边形的每一个内角都大于,小于;(3)多边形的外角和与边数无关.
知能解读(四)平面图形的镶嵌
用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫作用多边形覆盖平面(或平面镶嵌).
注意
(1)不论用同种正多边形还是用多种正多边形镶嵌平面,都必须满足围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角.
(2)用两种正多边形镶嵌,①正三角形和正方形;即一个顶点处需三个正三角形,两个正方形;②正三角形和正六边形;可以镶嵌成两种图形,一是一个顶点处有四个正三角形和一个正六边形,二是一个顶点处有两个正三角形和两个正六边形;③正三角形和正十二边形:即一个顶点处需一个正三角形和两个正十二边形;④正方形和正八边形:即一个顶点处需一个正方形和两个正八边形.
方法技巧归纳
方法技巧(一)利用多边形的内角和与外角和进行计算的方法
边形的内角和为,利用该公式,可以求一个多边形的内角和或边数.
方法技巧(二)利用多边形的外角和进行计算的方法
任意多边形的外角和都是,据此我们可以进行相关计算.
点拨
判断凸多边形的内角中锐角的个数一般从外角中钝角的个数入手.
方法技巧(三)利用多边形的对内角线条数公式求对角线条数或求多边形边数
对边有条对角线,利用这规律可以在已知多边形数时求对角线条数,也可以已知对角线条数求多边形的边数.
方法技巧(四)利用镶嵌的条件判断哪些图形能进行镶嵌
不论用一种多边形还是多种正多边形镶嵌地面,都必须满足周围一点拼在一起的几个多边形的内角和是
易混易错辨析
易混易错知识
多边形对角线条数与公式容易混淆.
因为从边形的每一个顶点都能引出条对角线,共有个顶点,但每条对角线都计算了两次,因此边形的对角线共有条.而我们学过的平面内条直线相交,最多有个交点;过不在同一直线上的个点,最多有条直线.
易混易错(一)因对镶嵌的概念理解不透而致错
易混易错(二)因把与混淆而致错
中考试题研究
中考命题规律
本讲在中考中主要考查多边形的内角和与外角和及利用镶嵌的知识解决一些实际问题,另外还考查学生的动手实践能力,题型以填空题、选择题为主.
中考试题(一)用多边形内角和外角和公式进行运算
中考试题(二)计算多边形对角线条数
三角形与多边形
考情分析
高频考点
考查频率
所占分值
1.三角形的三边关系
★★
3~5分
2.三角形的内角和
★★★
3.三角形外角的性质及推论
★
4.三角形中的角平分线、中线、高线的性质
★
5.多边形的内角和公式
★★
6.多边形的外角和
★
7.多边形的对角线条数
★
知能图谱
第34讲
三角形的有关概念
知识能力解读
知能截图(一)三角形及其相关概念
(1)定义:由不在同一条直线上的三条线段收尾顺次相接所组成的图形叫作三角形.
(2)相关概念:如图所示,线段是三角形的边.点是三角形的顶点,是相邻两边组成的角,叫作三角形的内角,简称三角形的角.
(3)表示方法:顶点是的三角形,记作,读作“三角形.”
(4)三角形的外角:三角形的一边与另一边的延长线组成的角,叫作三角形的外角.
知能解读(二)三角形的分类
(1)按角分:
(
三角形
)(2)按边分:
注意
不能把等边三角形算作是单独的一类,等腰三角形包括等边三角形,等边三角形是特殊的等腰三角形,即底边和腰相等的等腰三角形.
知能解读(三)三角形中的重要线段
1三角形的角平分线
三角形的一个角的平分线与这个角的对边相交,顶点和交点之间的线段叫作三角形的角平分线.
2三角形的中线
在三角形中,连接一个顶点和它的对边中点的线段叫作三角形的中线.
三角形的三条中线相交于一点,三角形三条中线的交点,叫作三角形的重心.
3三角形的高
从三角形的一个顶点向它的对边所在直线画垂线,顶点和垂足间的线段叫作三角形的高.
注意
(1)三角形中,角平分线、中线以及高都有三条,且分别都交于一点.
(2)这三种线都是线段.
(3)一个三角形中,①三条角平分线都在三角形内;②三条中线也都在三角形内;③三条高的位置:a.锐角三角形的三条高都在三角形内;b.直角三角形有两条高为直角边,斜边上的高在三角形内;c.钝角三角形有一条高在三角形内,另两条高在三角形外.
知能解读(四)三角形的三边关系
(1)三角形的和大于等三边,(2)三角形两边的差小于第三边.
注意
根据三角形的三边关系,只要比较两条线段的长度和大于最长线段的长度即可构成三角形.
知能解读(五)三角形的稳定性
如果三角形的三条边固定,那么三角形的形状和大小就完全确定了,三角形的这个特征叫作三角形的稳定性.除了三角形外,其他多边形不具备稳定性,因此在生产建设中,为达到稳固的目的,把一些部件都做成三角形结构.
知能解读(六)三角形中有关角的结论
(1)三角形内角和定理:三角形三个内角和等于.
(2)三角形的外角等于与它不相邻的两个内角的和.
(3)三角形的一个外角大于任何一个和它不相邻的内角.
(4)直角三角形的两个锐角互余;有两个角互余的三角形是直角三角形.
方法技巧归纳
方法技巧(一)利用三角形中角的关系求值与证明
三角形中求角的读数,涉及的知识点有三个:(1)三角形的内角和;(2)三角形的外角性质;(3)三角形的内角与相邻外角互补.
点拨
充分利用角平分线的性质和三角形的内外交的关系建立与的练习是解决问题的关键.
方法技巧(二)利用三角形三边关系判断是否能构成三角形
按照三角形三边关系去判断时必须满足任意两边之和大于第三边,而在实际使用时,只要其中较小的两条线段长度的和能够大于第三条线段的长度,就能构成三角形.
点拨
三条线段能否组成三角形,可用如下方法来进行判定:设三条线段的长为,并满足,若,则线段可以组成三角形.
方法技巧(三)利用三角形的三边关系确定第三边的取值范围
根据三角形两边和大于第三边,两边的差小于第三边,可得第三边应小于两边的和,并且大于两边的差.
点拨
已知三角形的两边长,可根据三边关系确定第三边的取值范围;另两边之差的绝对值<第三边<另两边之和.
方法技巧(四)利用三角形中线的概念证明面积相等
三角形的一条中线把原三角形分成两个三角形,根据垂线的性质可得到这两个三角形等底同高,因此其面积相等,利用这一特点可以证明有关的面积关系问题.
点拨
三角形的中线把它分成两个面积相等的三角形.
方法技巧(五)利用三角形的稳定性解决实际问题
把实际问题转化为三角形问题,用三角形的稳定性未解释.
方法技巧(六)三角形内角和的应用技巧
点拨
当要求的角度列式计算很复杂时,可以通过列方程求解,体现方程思想.
易混易错辨析
易混易错知识
1.角平分线和三角形的角平分线.
区别:角平分线是一条射线,而三角形的角平分线是一条线段.
2.三角形的角平分线、中线和高.
区别:三角形的角平分线是一个角的平分线和对边相交所构成的线段,而高是过一个顶点向对边所在直线作的垂线段.
易混易错(一)忽视三角形“三边关系”致错
易混易错(二)不能准确画出钝角三角形的三条高
中考试题研究
中考命题规律
三角形是历年中考的必考内容,考查热点是运用三角形的三边关系,内角和以及内外交之间的关系进行有关推力与计算,多以填空题、选择题的形式出现.
中考试题(一)三角形内角和的应用
中考试题(二)三角形中角的运算求解
中考试题(三)三角形三边关系的应用
第35讲
多边形的内角和与外角和
知识能力解读
知能解读(一)多边形的有关概念
1多边形的定义
在平面内,由一些线段首尾顺次相接组成的封闭图形叫作多边形.
注意
多边形根据边数的不同可分为三角形、四边形、五边形、…,我们所学的多边形都是凸多边形(整个图形都在任一边所在直线同旁的多边形),即组成多边形的每一个内角都大于,且小于.
2正多边形
各个角都相等,各条边都相等的多边形叫作正多边形,比如:等边三角形、正方形等.
3相关概念
(1)内角:多边形相邻两边组成的角叫作它的内角.
(2)外角:多边形的一边与它的邻边的延长线组成的角叫作多边形的外角.
(3)对角线:连接多边形不相邻的两个顶点的线段,叫作多边形的对角线.
注意
(1)一个边形从一个顶点出发有条对角线,所有对角线的条数是.
(2)把多边形转化成三角形求解的常用方法是连接对角线.
知能解读(二)多边形的内角和公式:边形的内角和等于
知能解读(三)多边形的外角和等于
注意
(1)多边形的外角和不随边数的变化而变化,但内角和随边数的变化而变化,且边数每增加1,内角和就增加;(2)多边形的每一个内角都大于,小于;(3)多边形的外角和与边数无关.
知能解读(四)平面图形的镶嵌
用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫作用多边形覆盖平面(或平面镶嵌).
注意
(1)不论用同种正多边形还是用多种正多边形镶嵌平面,都必须满足围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角.
(2)用两种正多边形镶嵌,①正三角形和正方形;即一个顶点处需三个正三角形,两个正方形;②正三角形和正六边形;可以镶嵌成两种图形,一是一个顶点处有四个正三角形和一个正六边形,二是一个顶点处有两个正三角形和两个正六边形;③正三角形和正十二边形:即一个顶点处需一个正三角形和两个正十二边形;④正方形和正八边形:即一个顶点处需一个正方形和两个正八边形.
方法技巧归纳
方法技巧(一)利用多边形的内角和与外角和进行计算的方法
边形的内角和为,利用该公式,可以求一个多边形的内角和或边数.
方法技巧(二)利用多边形的外角和进行计算的方法
任意多边形的外角和都是,据此我们可以进行相关计算.
点拨
判断凸多边形的内角中锐角的个数一般从外角中钝角的个数入手.
方法技巧(三)利用多边形的对内角线条数公式求对角线条数或求多边形边数
对边有条对角线,利用这规律可以在已知多边形数时求对角线条数,也可以已知对角线条数求多边形的边数.
方法技巧(四)利用镶嵌的条件判断哪些图形能进行镶嵌
不论用一种多边形还是多种正多边形镶嵌地面,都必须满足周围一点拼在一起的几个多边形的内角和是
易混易错辨析
易混易错知识
多边形对角线条数与公式容易混淆.
因为从边形的每一个顶点都能引出条对角线,共有个顶点,但每条对角线都计算了两次,因此边形的对角线共有条.而我们学过的平面内条直线相交,最多有个交点;过不在同一直线上的个点,最多有条直线.
易混易错(一)因对镶嵌的概念理解不透而致错
易混易错(二)因把与混淆而致错
中考试题研究
中考命题规律
本讲在中考中主要考查多边形的内角和与外角和及利用镶嵌的知识解决一些实际问题,另外还考查学生的动手实践能力,题型以填空题、选择题为主.
中考试题(一)用多边形内角和外角和公式进行运算
中考试题(二)计算多边形对角线条数
同课章节目录
