太原市数学中考《第十六章对称、平移与旋转》知识点聚焦
文档属性
| 名称 | 太原市数学中考《第十六章对称、平移与旋转》知识点聚焦 | 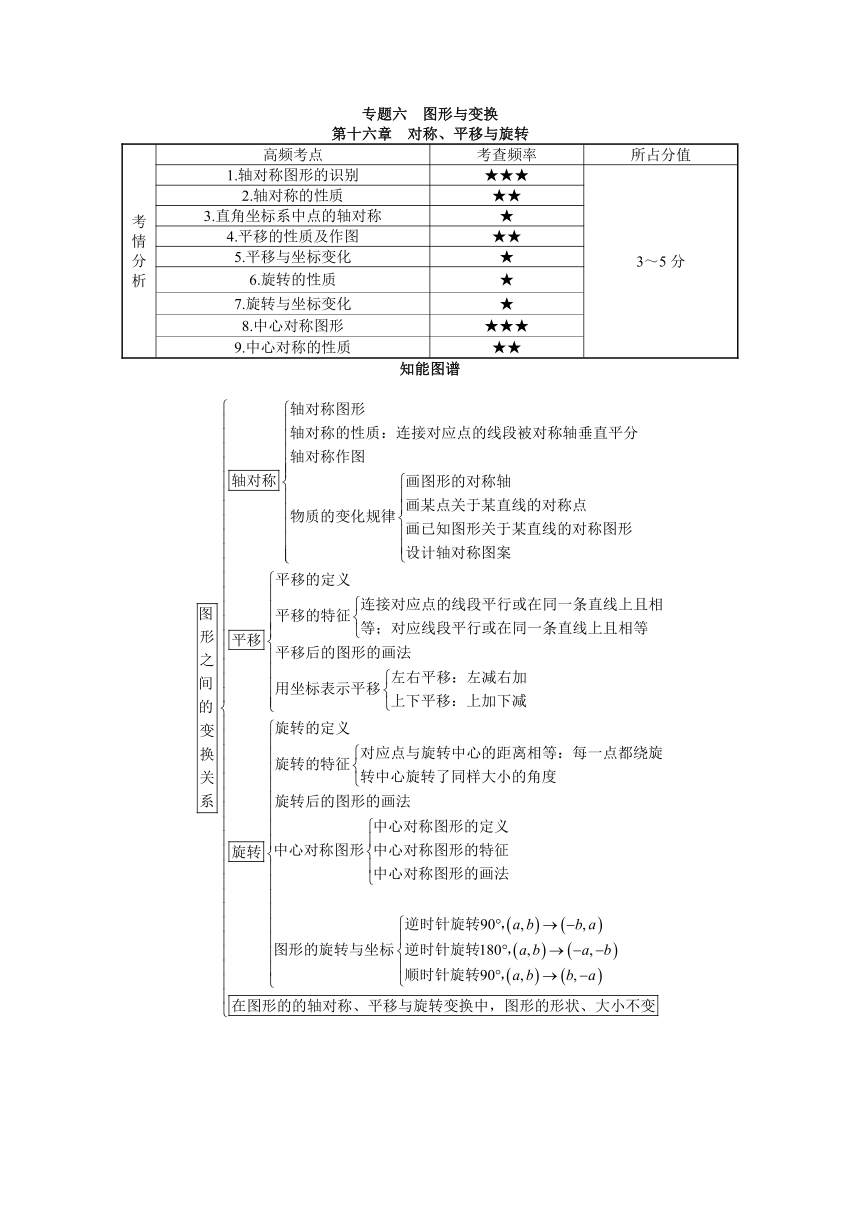 | |
| 格式 | zip | ||
| 文件大小 | 111.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-08 20:59:07 | ||
图片预览


文档简介
专题六
图形与变换
第十六章
对称、平移与旋转
考情分析
高频考点
考查频率
所占分值
1.轴对称图形的识别
★★★
3~5分
2.轴对称的性质
★★
3.直角坐标系中点的轴对称
★
4.平移的性质及作图
★★
5.平移与坐标变化
★
6.旋转的性质
★
7.旋转与坐标变化
★
8.中心对称图形
★★★
9.中心对称的性质
★★
知能图谱
第36讲
轴对称
知识能力解读
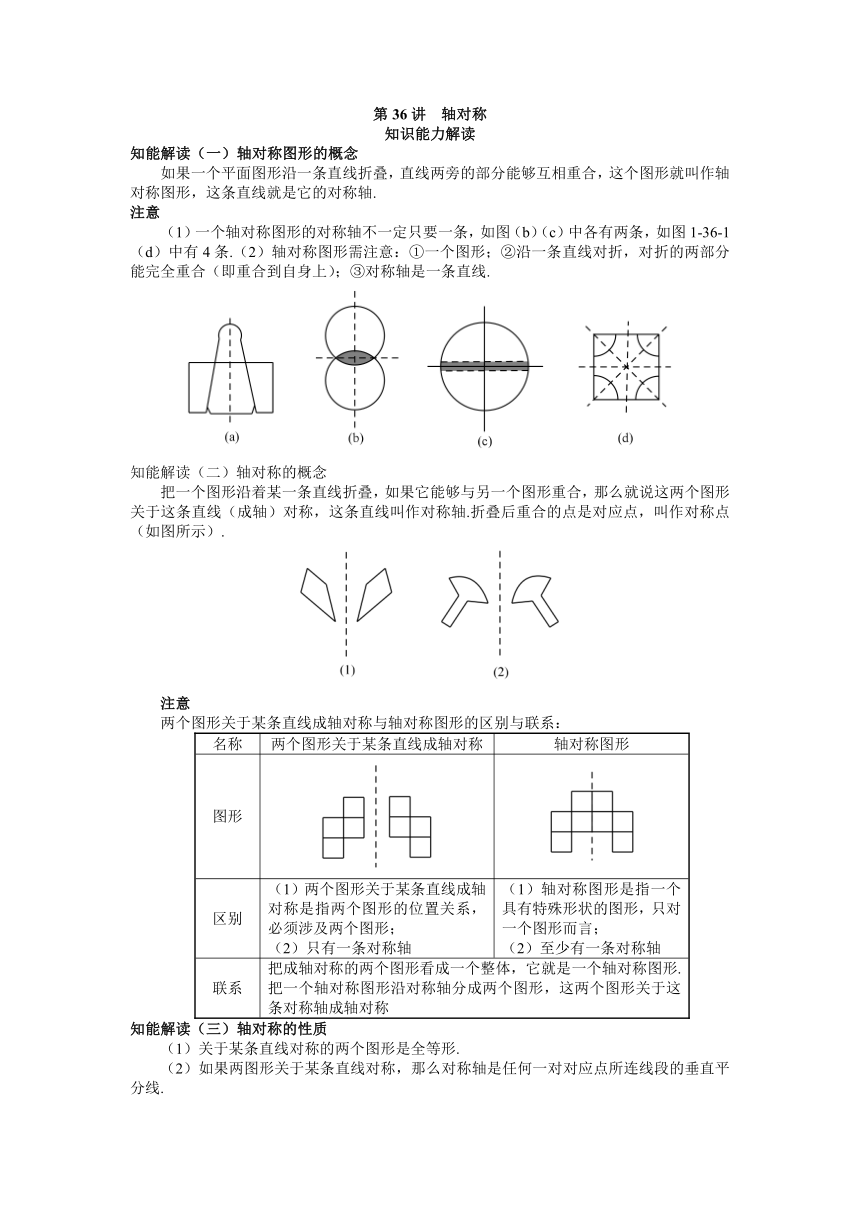
知能解读(一)轴对称图形的概念
如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫作轴对称图形,这条直线就是它的对称轴.
注意
(1)一个轴对称图形的对称轴不一定只要一条,如图(b)(c)中各有两条,如图1-36-1(d)中有4条.(2)轴对称图形需注意:①一个图形;②沿一条直线对折,对折的两部分能完全重合(即重合到自身上);③对称轴是一条直线.
知能解读(二)轴对称的概念
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称,这条直线叫作对称轴.折叠后重合的点是对应点,叫作对称点(如图所示).
注意
两个图形关于某条直线成轴对称与轴对称图形的区别与联系:
名称
两个图形关于某条直线成轴对称
轴对称图形
图形
区别
(1)两个图形关于某条直线成轴对称是指两个图形的位置关系,必须涉及两个图形;
(2)只有一条对称轴
(1)轴对称图形是指一个具有特殊形状的图形,只对一个图形而言;
(2)至少有一条对称轴
联系
把成轴对称的两个图形看成一个整体,它就是一个轴对称图形.把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条对称轴成轴对称
知能解读(三)轴对称的性质
(1)关于某条直线对称的两个图形是全等形.
(2)如果两图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
注意
全等的图形不一定是成轴对称的,成轴对称的图形一定是全等的,所以成轴对称的两个图形中,对应线段相等,对应角相等.
知能解读(四)轴对称作(画)图
1画图形的对称轴
(1)如果两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线,因此我们只要找到一对对应点,作出连接它们的线段的垂直平分线,就可以得到这个图形的对称轴.
(2)对于轴对称图形,只要找到任意一对对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴.
注意
找对称点时,所找对称点最好是图形的顶点或拐点,这样作出的图形更准确.
2画轴对称图形
(1)由一个平面图形可以得到与它关于一条直线对称的图形,这个图形与原图形的形状、大小完全相同;新图形上的每一点都是原图形上的某一点关于直线的对称点;连接任意一对对应点的线段被对称轴垂直平分.
(2)几何图形都可以看作是由点组成.对于某些图形,只要画出图形中的一些特殊点(如线段的端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
(3)画轴对称图形的步骤;
①确定原图形的特殊点;
②作出所有特殊点关于对称轴的对称点;
③按原图形的顺序顺次连接相应的对称点.
注意
“特殊点”是指能确定图形形状、大小及位置的关键点.如果是多边形,这些点就是指所有的顶点;如果是线段,这些点就是指线段的两个端点等.
知能解读(五)设计轴对称图案
应用轴对称知识,设计美观大方的图形,有利于增强对轴对称知识的理解,提高审美能力和创作设计能力.以图中的(a)为例进行说明.
步骤如下:
(1)准备一张圆形纸片;
(2)在圆形纸片上画两条互相垂直的直径,如图(b);
(3)如图(c),在其中画出四边形;
(4)如图(d),在其中画出四边形关于铅直对称轴的对称四边形;
(5)如图(e),画出图(d)中的图形关于水平对称轴的对称图形;
(6)在图(e)中图上颜色.
这样就完成这幅轴对称图案了.
知能解读(六)关于坐标轴对称的点的坐标关系
在直角坐标系中,点关于轴的对称点是,关于轴的对称点是;
关于坐标轴成轴对称的点的坐标特征;
(1)关于轴(横轴)对称的点:横坐标相同,纵坐标互为相反数,即“横同纵反”;
(2)关于轴(纵轴)对称的点:纵坐标相同,横坐标互为相反数,即“纵同横反”.
方法技巧归纳
方法技巧(一)轴对称图形及其对称轴的识别方法
判断一个图形是不是轴对称图形,可以用折纸的方法按照轴对称图形的概念,看是否能找到一条直线,将图形沿其折叠,使直线两旁的部分能够完全重合(即用轴对称图形的定义进行识别).
点拨
识别轴对称图形的关键是找到作为对称轴的直线,沿直线折叠后两边的部分能够重合,有时这样的直线能够找到多条,说明这个轴对称图形有多条对称轴.
方法技巧(二)利用轴对称图形的性质求角的度数或线段的长的方法
由于轴对称图形沿对称轴翻折后两边互相重合,而重合的边或角存在相等关系,所以根据这一特点可以进行线段或角的计算.
点拨
解此类题的关键是找准折叠后重合的角、重合的边,利用存在的相等关系解决问题.
点拨
利用轴对称的性质时,关键是找对应点,这样问题就能化解难为易,化繁为简.
方法技巧(三)轴对称作图
利用轴对称的性质时,可以确定成轴对称的图形的对称轴,也可以作出一个图形关于一条直线的轴对称图形.
点拨
点在对称轴上时,它关于对称轴的对称点也在对称轴上;点在对称轴一侧时,它关于对称轴的对称点在对称轴的另一侧.
方法技巧(四)生活中的轴对称
解决平面内最短(最小)距离问题,可以利用轴对称对作出其中一点关于直线的对称点,转化为“两点之间,线段最短”来解决.
易混易错辨析
易混易错知识
1.轴对称与轴对称图形
区别:轴对称是对两个图形来说的,它是两个全等图形之间的一种位置关系,而轴对称图形是对一个图形来说的,它是一个图形所具备的一种特征.
2.判断成轴对称时,误以为只要两个图形就可以.
易混易错
找成轴对称的图形时,由于对称轴对称的概念理解不正确而致误
中考试题研究
中考命题规律
中考中对称轴对称的考查主要以识别轴对称图形和点在坐标系中的轴对称为主,也考查利用轴对称求最短路线的应用,题型以填空题、选择题为主,也有作图题.
中考试题(一)识别轴对称图形
点拨
利用轴对称图形的定义判断,沿某条直线折叠看直线两旁的部分能否完全重合.
中考试题(二)点关于坐标轴的对称点的坐标
中考试题(三)用轴对称求最短路线问题
第37讲
平移与旋转
知识能力解读
知能解读(一)平移的概念和特征
1平移的概念
把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同,图形的这种移动,叫作平移.
点拨
(1)图形平移的两个要素:一是平移的方向;二是平移的距离;
(2)图形平移的方向不限于是水平的.
2平移的特征
(1)平移后得到的新图形与原图形的形状和大小完全相同.
(2)新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点,连接各组对应点的线段平行(或在同一条直线上)且相等.
注意
(1)由平移性质可知:连接对应点线段的长度就是图形平移的距离.
(2)区分对应点的连续和对应线段,在平移过程中对应线段和对应点的连线都有可能在同一条直线上.
知能解读(二)画平移后的图形的步骤方法
(1)确定平移的方向;(2)确定平移的距离;(3)画出决定图形大小和形状的对应点、对应角或对应线段;(4)按原来图形的连接方式补充完整图形.
知能解读(三)平面直角坐标系汇总的平移
一般地,在平面直角坐标系中,将点向右或左平移个单位长度,可以得到对应点或;将点向上或下平移个单位长度,可以得到对应点或.
一般地,在平面直角坐标系中,如果把一个图形各个点的横坐标都加上(或减去)一个正数,相应的新图形就是把原图形向右(或向左)平移个单位长度;如果把它各个点的纵坐标都加上(或减去)一个正数,相应的新图形就是把原图形向上(或向下)平移个单位长度.
知能解读(四)旋转的概念和特征
1旋转的概念
把一个平面图形绕着平面内某一点转动一个角度,叫作图形的旋转.点叫作旋转中心,转动的角叫作旋转角.如图形上的点经过旋转变化点,那么这两个点叫作这个旋转的对应点.
如图所示,是绕定点逆时针旋转得到的,其中点与点叫作对应点,线段与线段叫作对应线段,与叫作对应角,点叫作旋转中心,(或)的度数叫作旋转的角度.图形的旋转由旋转中心、旋转方向与旋转的角度所决定.
点拨
图形旋转的三要素是旋转中心、旋转方向和旋转角.
2旋转的特征
(1)对应点到旋转中心的距离相等;
(2)对应点与旋转中心所连线段的夹角等于旋转角;
(3)旋转前、后的图形全等.
注意
(1)旋转角与对应角不同,旋转角是指图形旋转过的角,而不是图形中的角;对应角是指图形旋转前后能够重合的角,它是图形中的角.(2)对应点到旋转中心的距离与对应线段的长度不同,对应点到旋转中心的距离是图形上的点到旋转中心的距离;对应线段则是图形上的线段.
3旋转作图的步骤方法
(1)确定旋转中心、旋转方向、旋转角;(2)找出图形上的关键点;(3)连接图形上的关键点与旋转中心,然后按旋转方向分别将它们旋转一定的角度,得到关键点的对应点;(4)按原图的顺序连接这些对应点,即得旋转后的图形.
知能解读(五)平移、旋转与轴对称的关系
变换
异同
平
移
旋
转
对称轴
不同点
平移变换前后,两个图形的对应线段平行(或在同一条直线上),对应角的两边分别平行(或在同一条直线上)且方向一致
旋转变换前后,两个图形后,两个图形的任意一个对对应点与旋转中心所连线段的夹角都是旋转角
若成轴对称的两个图形的对应线段或其延长线段相交,则其交点在对称轴上;成轴对称的两个图形的对应点所连线段被称对称轴垂直平分
相同点
(1)都是在平面进行的图形变换;
(2)都是只改变图形的位置,不改变图形的形状和大小,即变换前后图形的对应边相等,对应角相等,两图形全等;
(3)都是把一个已知图形变换后得到另一个图形
知能解读(六)中心对称与中心对称图形的概念
1中心对称
把一个图形绕着某一点旋转,如图它能够与另一个图形重合,那么就说这两个U形关于这个点对称或中心对称,这个点叫作对称中心(简称中心).这两个图形再旋转后能重合的对应点叫作关于对称中心的对称点.如图,绕着点旋转后,与完全重合,则称和关于点对称,点是点关于点的对称点.
2中心对称图形
把一个图形绕着某一个点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形叫作中心对称图形,这个点就是它的对称中心.
中心对称与中心对称图形的区别与联系:
中心对称
中心对称图形
区别
(1)是针对两个图形而言的.
(2)是指两个图形的(位置)关系.
(3)对称点在两个图形上.
(4)对称中心在两个图形之间.
(1)是针对一个图形而言的.
(2)是指具有某种性质的一个图形.
(3)对称点在一个图形上.
(4)对称中心在图形上.
联系
(1)都是通过把图形旋转重合来定义的.(2)两者可以相互转化,如果把中心对称的两个图形看成一个整体(一个图形),那么这“一个图形”就是中心对称图形;反过来,如果把一个中心对称图形相互对称的两部分看成两个图形,那么这“两个图形”中心对称
知能解读(七)中心对称的性质
(1)中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分;
(2)中心对称的两个图形是全等图形.
知能解读(八)作中心对称图形的一般步骤
(1)作出已知图形各顶点(或决定图形形状的关键点)关于中心的对称点——连接关键点和中心,并延长一倍确定关键的对称点.
(2)把各对称点按已知图形的连接方式依次连接起来,则所得到的图形就是已知图形关于对称中心对称的图形.
知能解读(九)找对称中心的方法和步骤
对于中心对称图形和关于某一点对称的两个图形,它们的对称中心非常重要,找不对称中心是解决先关问题的关键.由中心对称的特征可知,对称中心为对应点连线的中点或两组相对应点连线的交点,因此找对称中心的步骤如下:
方法1:连接两个对应点,取对应点连线的中点,则中点为对称中心.
方法2:连接两个对应点,在连接两个对应点,两组对应点连线的交点为对称中心.
方法技巧归纳
方法技巧(一)平移现象的识别方法
识别时应把握两点:一是平移是沿直线进行的;而是平移只改变位置,不敢变形状和大小
.
点拨
(1)平移是由平移的方向和距离决定的(即平移的两个要素).
(2)平移不改变图形的形状和大小,只改变位置.
方法技巧(二)图形的平移与坐标
将直角坐标系中的点向右(或向左)平移个单位长度,点的纵坐标不变,横坐标增加(或减少)个单位.将直角坐标系中的点向上(或向下)平移个单位长度,点的横坐标不变,纵坐标增加(或减少)个单位.
点拨
图形向左(或向右)平移,则横坐标减去(或加上)某一个数,纵坐标不变;图形向上(或向下)平移,则纵坐标加上(或减去)某一个数,横坐标不变.
方法技巧(三)选择性质的应用技巧
一个图形旋转后得到一个新图形,只是位置发生改变,对应线段相等,对应角相等,利用其性质可进行相关计算.
方法技巧(四)中心对称图形的识别
对中心对称图形的理解应注意以下三点:(1)围绕某点;(2)旋转;(3)与本身重合.这是判定一个图形是不是中心对称图形的重要依据.
方法技巧(五)综合运用轴对称、平移与宣战作图的方法
首先要熟练掌握它们各自的作法,然后对照题目中的具体要求一步一步进行操作.
点拨
平移、旋转、轴对称作图时,只需把多边形的各个顶点等关键点的对应点作出,再顺次连成对变形即可.
易混易错辨析
易混易错知识
中心对称和中心对称图形的区别:
(1)中心对称是指两个图形的位置关系,而中心对称图形是指具有某种性质的图形;(2)成中心对称的两个图形的对称点分别在两个图形上,而中心非常图形的对称点在一个图形上;(3)中心对称图个的对称中心一定在这个图形的内部,而成中心对称的两个图形的对称中心可以在这两个图形的外部,也可以在这两个图形的内部,还可以在它们的公共边上.
易混易错(一)对平移的性质理解不透而出错
易混易错(二)旋转方向不清楚易出现漏解
中考试题研究
中考命题规律
近几年来,平移与旋转越来越受重视,因为它与“实际应用”联系密切,同时又非常简单的证明方法.新课程标准又强化了对平移、旋转、中心对称等知识的考场,纵观近两年各地中考题,此类内容所占比例大大增加.
中考试题(一)轴对称图形和中心对称图形的识别
中考试题(二)平移与旋转中的有关计算
中考试题(三)平移或旋转作图
图形与变换
第十六章
对称、平移与旋转
考情分析
高频考点
考查频率
所占分值
1.轴对称图形的识别
★★★
3~5分
2.轴对称的性质
★★
3.直角坐标系中点的轴对称
★
4.平移的性质及作图
★★
5.平移与坐标变化
★
6.旋转的性质
★
7.旋转与坐标变化
★
8.中心对称图形
★★★
9.中心对称的性质
★★
知能图谱
第36讲
轴对称
知识能力解读
知能解读(一)轴对称图形的概念
如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫作轴对称图形,这条直线就是它的对称轴.
注意
(1)一个轴对称图形的对称轴不一定只要一条,如图(b)(c)中各有两条,如图1-36-1(d)中有4条.(2)轴对称图形需注意:①一个图形;②沿一条直线对折,对折的两部分能完全重合(即重合到自身上);③对称轴是一条直线.
知能解读(二)轴对称的概念
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称,这条直线叫作对称轴.折叠后重合的点是对应点,叫作对称点(如图所示).
注意
两个图形关于某条直线成轴对称与轴对称图形的区别与联系:
名称
两个图形关于某条直线成轴对称
轴对称图形
图形
区别
(1)两个图形关于某条直线成轴对称是指两个图形的位置关系,必须涉及两个图形;
(2)只有一条对称轴
(1)轴对称图形是指一个具有特殊形状的图形,只对一个图形而言;
(2)至少有一条对称轴
联系
把成轴对称的两个图形看成一个整体,它就是一个轴对称图形.把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条对称轴成轴对称
知能解读(三)轴对称的性质
(1)关于某条直线对称的两个图形是全等形.
(2)如果两图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
注意
全等的图形不一定是成轴对称的,成轴对称的图形一定是全等的,所以成轴对称的两个图形中,对应线段相等,对应角相等.
知能解读(四)轴对称作(画)图
1画图形的对称轴
(1)如果两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线,因此我们只要找到一对对应点,作出连接它们的线段的垂直平分线,就可以得到这个图形的对称轴.
(2)对于轴对称图形,只要找到任意一对对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴.
注意
找对称点时,所找对称点最好是图形的顶点或拐点,这样作出的图形更准确.
2画轴对称图形
(1)由一个平面图形可以得到与它关于一条直线对称的图形,这个图形与原图形的形状、大小完全相同;新图形上的每一点都是原图形上的某一点关于直线的对称点;连接任意一对对应点的线段被对称轴垂直平分.
(2)几何图形都可以看作是由点组成.对于某些图形,只要画出图形中的一些特殊点(如线段的端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
(3)画轴对称图形的步骤;
①确定原图形的特殊点;
②作出所有特殊点关于对称轴的对称点;
③按原图形的顺序顺次连接相应的对称点.
注意
“特殊点”是指能确定图形形状、大小及位置的关键点.如果是多边形,这些点就是指所有的顶点;如果是线段,这些点就是指线段的两个端点等.
知能解读(五)设计轴对称图案
应用轴对称知识,设计美观大方的图形,有利于增强对轴对称知识的理解,提高审美能力和创作设计能力.以图中的(a)为例进行说明.
步骤如下:
(1)准备一张圆形纸片;
(2)在圆形纸片上画两条互相垂直的直径,如图(b);
(3)如图(c),在其中画出四边形;
(4)如图(d),在其中画出四边形关于铅直对称轴的对称四边形;
(5)如图(e),画出图(d)中的图形关于水平对称轴的对称图形;
(6)在图(e)中图上颜色.
这样就完成这幅轴对称图案了.
知能解读(六)关于坐标轴对称的点的坐标关系
在直角坐标系中,点关于轴的对称点是,关于轴的对称点是;
关于坐标轴成轴对称的点的坐标特征;
(1)关于轴(横轴)对称的点:横坐标相同,纵坐标互为相反数,即“横同纵反”;
(2)关于轴(纵轴)对称的点:纵坐标相同,横坐标互为相反数,即“纵同横反”.
方法技巧归纳
方法技巧(一)轴对称图形及其对称轴的识别方法
判断一个图形是不是轴对称图形,可以用折纸的方法按照轴对称图形的概念,看是否能找到一条直线,将图形沿其折叠,使直线两旁的部分能够完全重合(即用轴对称图形的定义进行识别).
点拨
识别轴对称图形的关键是找到作为对称轴的直线,沿直线折叠后两边的部分能够重合,有时这样的直线能够找到多条,说明这个轴对称图形有多条对称轴.
方法技巧(二)利用轴对称图形的性质求角的度数或线段的长的方法
由于轴对称图形沿对称轴翻折后两边互相重合,而重合的边或角存在相等关系,所以根据这一特点可以进行线段或角的计算.
点拨
解此类题的关键是找准折叠后重合的角、重合的边,利用存在的相等关系解决问题.
点拨
利用轴对称的性质时,关键是找对应点,这样问题就能化解难为易,化繁为简.
方法技巧(三)轴对称作图
利用轴对称的性质时,可以确定成轴对称的图形的对称轴,也可以作出一个图形关于一条直线的轴对称图形.
点拨
点在对称轴上时,它关于对称轴的对称点也在对称轴上;点在对称轴一侧时,它关于对称轴的对称点在对称轴的另一侧.
方法技巧(四)生活中的轴对称
解决平面内最短(最小)距离问题,可以利用轴对称对作出其中一点关于直线的对称点,转化为“两点之间,线段最短”来解决.
易混易错辨析
易混易错知识
1.轴对称与轴对称图形
区别:轴对称是对两个图形来说的,它是两个全等图形之间的一种位置关系,而轴对称图形是对一个图形来说的,它是一个图形所具备的一种特征.
2.判断成轴对称时,误以为只要两个图形就可以.
易混易错
找成轴对称的图形时,由于对称轴对称的概念理解不正确而致误
中考试题研究
中考命题规律
中考中对称轴对称的考查主要以识别轴对称图形和点在坐标系中的轴对称为主,也考查利用轴对称求最短路线的应用,题型以填空题、选择题为主,也有作图题.
中考试题(一)识别轴对称图形
点拨
利用轴对称图形的定义判断,沿某条直线折叠看直线两旁的部分能否完全重合.
中考试题(二)点关于坐标轴的对称点的坐标
中考试题(三)用轴对称求最短路线问题
第37讲
平移与旋转
知识能力解读
知能解读(一)平移的概念和特征
1平移的概念
把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同,图形的这种移动,叫作平移.
点拨
(1)图形平移的两个要素:一是平移的方向;二是平移的距离;
(2)图形平移的方向不限于是水平的.
2平移的特征
(1)平移后得到的新图形与原图形的形状和大小完全相同.
(2)新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点,连接各组对应点的线段平行(或在同一条直线上)且相等.
注意
(1)由平移性质可知:连接对应点线段的长度就是图形平移的距离.
(2)区分对应点的连续和对应线段,在平移过程中对应线段和对应点的连线都有可能在同一条直线上.
知能解读(二)画平移后的图形的步骤方法
(1)确定平移的方向;(2)确定平移的距离;(3)画出决定图形大小和形状的对应点、对应角或对应线段;(4)按原来图形的连接方式补充完整图形.
知能解读(三)平面直角坐标系汇总的平移
一般地,在平面直角坐标系中,将点向右或左平移个单位长度,可以得到对应点或;将点向上或下平移个单位长度,可以得到对应点或.
一般地,在平面直角坐标系中,如果把一个图形各个点的横坐标都加上(或减去)一个正数,相应的新图形就是把原图形向右(或向左)平移个单位长度;如果把它各个点的纵坐标都加上(或减去)一个正数,相应的新图形就是把原图形向上(或向下)平移个单位长度.
知能解读(四)旋转的概念和特征
1旋转的概念
把一个平面图形绕着平面内某一点转动一个角度,叫作图形的旋转.点叫作旋转中心,转动的角叫作旋转角.如图形上的点经过旋转变化点,那么这两个点叫作这个旋转的对应点.
如图所示,是绕定点逆时针旋转得到的,其中点与点叫作对应点,线段与线段叫作对应线段,与叫作对应角,点叫作旋转中心,(或)的度数叫作旋转的角度.图形的旋转由旋转中心、旋转方向与旋转的角度所决定.
点拨
图形旋转的三要素是旋转中心、旋转方向和旋转角.
2旋转的特征
(1)对应点到旋转中心的距离相等;
(2)对应点与旋转中心所连线段的夹角等于旋转角;
(3)旋转前、后的图形全等.
注意
(1)旋转角与对应角不同,旋转角是指图形旋转过的角,而不是图形中的角;对应角是指图形旋转前后能够重合的角,它是图形中的角.(2)对应点到旋转中心的距离与对应线段的长度不同,对应点到旋转中心的距离是图形上的点到旋转中心的距离;对应线段则是图形上的线段.
3旋转作图的步骤方法
(1)确定旋转中心、旋转方向、旋转角;(2)找出图形上的关键点;(3)连接图形上的关键点与旋转中心,然后按旋转方向分别将它们旋转一定的角度,得到关键点的对应点;(4)按原图的顺序连接这些对应点,即得旋转后的图形.
知能解读(五)平移、旋转与轴对称的关系
变换
异同
平
移
旋
转
对称轴
不同点
平移变换前后,两个图形的对应线段平行(或在同一条直线上),对应角的两边分别平行(或在同一条直线上)且方向一致
旋转变换前后,两个图形后,两个图形的任意一个对对应点与旋转中心所连线段的夹角都是旋转角
若成轴对称的两个图形的对应线段或其延长线段相交,则其交点在对称轴上;成轴对称的两个图形的对应点所连线段被称对称轴垂直平分
相同点
(1)都是在平面进行的图形变换;
(2)都是只改变图形的位置,不改变图形的形状和大小,即变换前后图形的对应边相等,对应角相等,两图形全等;
(3)都是把一个已知图形变换后得到另一个图形
知能解读(六)中心对称与中心对称图形的概念
1中心对称
把一个图形绕着某一点旋转,如图它能够与另一个图形重合,那么就说这两个U形关于这个点对称或中心对称,这个点叫作对称中心(简称中心).这两个图形再旋转后能重合的对应点叫作关于对称中心的对称点.如图,绕着点旋转后,与完全重合,则称和关于点对称,点是点关于点的对称点.
2中心对称图形
把一个图形绕着某一个点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形叫作中心对称图形,这个点就是它的对称中心.
中心对称与中心对称图形的区别与联系:
中心对称
中心对称图形
区别
(1)是针对两个图形而言的.
(2)是指两个图形的(位置)关系.
(3)对称点在两个图形上.
(4)对称中心在两个图形之间.
(1)是针对一个图形而言的.
(2)是指具有某种性质的一个图形.
(3)对称点在一个图形上.
(4)对称中心在图形上.
联系
(1)都是通过把图形旋转重合来定义的.(2)两者可以相互转化,如果把中心对称的两个图形看成一个整体(一个图形),那么这“一个图形”就是中心对称图形;反过来,如果把一个中心对称图形相互对称的两部分看成两个图形,那么这“两个图形”中心对称
知能解读(七)中心对称的性质
(1)中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分;
(2)中心对称的两个图形是全等图形.
知能解读(八)作中心对称图形的一般步骤
(1)作出已知图形各顶点(或决定图形形状的关键点)关于中心的对称点——连接关键点和中心,并延长一倍确定关键的对称点.
(2)把各对称点按已知图形的连接方式依次连接起来,则所得到的图形就是已知图形关于对称中心对称的图形.
知能解读(九)找对称中心的方法和步骤
对于中心对称图形和关于某一点对称的两个图形,它们的对称中心非常重要,找不对称中心是解决先关问题的关键.由中心对称的特征可知,对称中心为对应点连线的中点或两组相对应点连线的交点,因此找对称中心的步骤如下:
方法1:连接两个对应点,取对应点连线的中点,则中点为对称中心.
方法2:连接两个对应点,在连接两个对应点,两组对应点连线的交点为对称中心.
方法技巧归纳
方法技巧(一)平移现象的识别方法
识别时应把握两点:一是平移是沿直线进行的;而是平移只改变位置,不敢变形状和大小
.
点拨
(1)平移是由平移的方向和距离决定的(即平移的两个要素).
(2)平移不改变图形的形状和大小,只改变位置.
方法技巧(二)图形的平移与坐标
将直角坐标系中的点向右(或向左)平移个单位长度,点的纵坐标不变,横坐标增加(或减少)个单位.将直角坐标系中的点向上(或向下)平移个单位长度,点的横坐标不变,纵坐标增加(或减少)个单位.
点拨
图形向左(或向右)平移,则横坐标减去(或加上)某一个数,纵坐标不变;图形向上(或向下)平移,则纵坐标加上(或减去)某一个数,横坐标不变.
方法技巧(三)选择性质的应用技巧
一个图形旋转后得到一个新图形,只是位置发生改变,对应线段相等,对应角相等,利用其性质可进行相关计算.
方法技巧(四)中心对称图形的识别
对中心对称图形的理解应注意以下三点:(1)围绕某点;(2)旋转;(3)与本身重合.这是判定一个图形是不是中心对称图形的重要依据.
方法技巧(五)综合运用轴对称、平移与宣战作图的方法
首先要熟练掌握它们各自的作法,然后对照题目中的具体要求一步一步进行操作.
点拨
平移、旋转、轴对称作图时,只需把多边形的各个顶点等关键点的对应点作出,再顺次连成对变形即可.
易混易错辨析
易混易错知识
中心对称和中心对称图形的区别:
(1)中心对称是指两个图形的位置关系,而中心对称图形是指具有某种性质的图形;(2)成中心对称的两个图形的对称点分别在两个图形上,而中心非常图形的对称点在一个图形上;(3)中心对称图个的对称中心一定在这个图形的内部,而成中心对称的两个图形的对称中心可以在这两个图形的外部,也可以在这两个图形的内部,还可以在它们的公共边上.
易混易错(一)对平移的性质理解不透而出错
易混易错(二)旋转方向不清楚易出现漏解
中考试题研究
中考命题规律
近几年来,平移与旋转越来越受重视,因为它与“实际应用”联系密切,同时又非常简单的证明方法.新课程标准又强化了对平移、旋转、中心对称等知识的考场,纵观近两年各地中考题,此类内容所占比例大大增加.
中考试题(一)轴对称图形和中心对称图形的识别
中考试题(二)平移与旋转中的有关计算
中考试题(三)平移或旋转作图
同课章节目录
