1.3.1 且 与 或 课件
图片预览











文档简介
课件42张PPT。常用逻辑用语第一章1.3 简单的逻辑联结词
“且”与“或”第一章1.了解逻辑联结词“且”、“或”的意义,会用联结词“且”、“或”联结或改写某些数学命题,会判断命题“p且q”、“p或q”的真假.
2.能把文字语言,符号语言相互转化.重点:了解“且”与“或”的含义,能判定由“且”、“或”组成的新命题的真假.
难点:对“或”的含义的理解1.一般地,用联结词“且”把命题p和q联结起来,就得到一个新命题,记作________,读作________.
2.关于逻辑联结词“且”
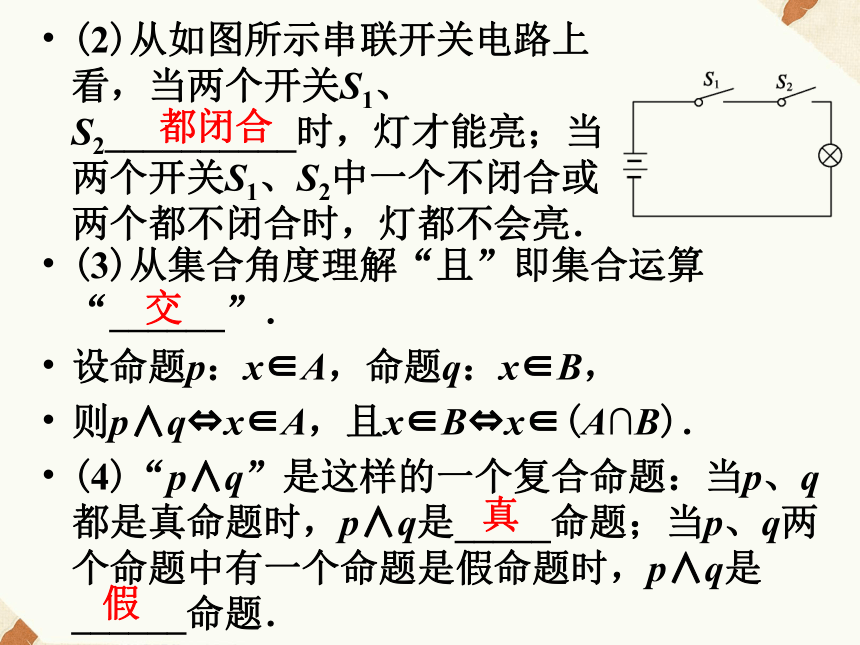
(1)“且”的含义与日常语言中的“并且”、“及”、“和”相当,是连词“既……又……”的意思,二者须_______成立.逻辑联结词“且”新知导学 p∧qp且q同时(2)从如图所示串联开关电路上看,当两个开关S1、S2__________时,灯才能亮;当两个开关S1、S2中一个不闭合或两个都不闭合时,灯都不会亮.都闭合(3)从集合角度理解“且”即集合运算“______”.
设命题p:x∈A,命题q:x∈B,
则p∧q?x∈A,且x∈B?x∈(A∩B).
(4)“p∧q”是这样的一个复合命题:当p、q都是真命题时,p∧q是_____命题;当p、q两个命题中有一个命题是假命题时,p∧q是______命题.交真假
牛刀小试
1.“xy≠0”是指( )
A.x≠0且y≠0
B.x≠0或y≠0
C.x,y至少一个不为0
D.不都是0
[答案] A
[解析] xy≠0当且仅当x≠0且y≠0.2.p:点P在直线y=2x-3上;q:点P在曲线y=-x2上,则使“p∧q”为真命题的一个点P(x,y)是( )
A.(0,-3) B.(1,2)
C.(1,-1) D.(-1,1)
[答案] C3.一般地,用联结词“或”把命题p和q联结起来,就得到一个新命题,记作_______,读作________.
4.关于逻辑联结词“或”
(1)“或”的含义和日常语言中的“或者”相当.是“要么……要么……”的意义,二者中有________成立即可.
(2)从并联开关电路上看,当两个开关S1、S2至少有一个闭合时,灯就亮,只有当两个开关S1和S2__________时,灯才不会亮.逻辑联结词“或”新知导学 p∨qp或q一个都断开(3)从集合角度理解“或”即集合运算“_____”.
设命题p:x∈A,命题q:x∈B,
则p∨q?x∈A,或x∈B?x∈(A∪B).并(4)当p、q两个命题有一个命题是真命题时,p∨q是_____命题;当p、q两个命题都是假命题时,p∨q是______命题.
逻辑联结词“或”与自然语言中的“或者”、“可能”相当,但自然语言中的“或者”有两种用法:一是“不可兼”的“或”;二是“可兼”的“或”,而我们仅研究可兼“或”在数学中的含义.真假牛刀小试
3.下列判断正确的是( )
A.命题p为真命题,命题“p或q”不一定是真命题
B.命题“p且q”是真命题时,命题p一定是真命题
C.命题“p且q”是假命题,命题p一定是假命题
D.命题p是假命题,命题“p且q”不一定是假命题
[答案] B
[解析] 因为p、q都为真命题时,“p且q”为真命题.4.由下列各组命题构成的新命题“p或q”、“p且q”都为真命题的是( )
A.p:4+4=9,q:7>4
B.p:a∈{a,b,c},q:{a}?{a,b,c}
C.p:15是质数,q:8是12的约数
D.p:2是偶数,q:2不是质数
[答案] B
[解析] “p或q”“p且q”都为真,则p真q真,故选B.5.给出如下条件:
(1)“p成立,q不成立”;
(2)“p不成立,q成立”;
(3)“p与q都成立”;
(4)“p与q都不成立”.
其中能使“p或q”成立的是________(填序号).
[答案] (1)(2)(3)命题的构成形式 [分析] 本题考查命题的构成形式,是本节课的重点,也是以后学习的基础.
[解析] (1)这个命题是“p且q”的形式,其中,p:小李是老师;q:小赵是老师.
(2)这个命题是“p或q”的形式,其中,p:1是合数;q:1是质数.
(3)这个命题是“p且q”的形式,其中,p:他是运动员;q:他是教练员.
(4)这个命题是“p且q”的形式,其中,p:这些文学作品艺术上有缺点;q:这些文学作品政治上有错误.[方法规律总结] 1.辨别复合命题的构成形式时,应根据组成复合命题的语句中所出现的逻辑联结词,或语句的意义确定复合命题的形式.
2.准确理解语义应注意抓住一些关键词.如“是…也是…”“兼”,“不但…而且…”,“既…又…”,“要么…,要么…”,“不仅…还…”等.
3.要注意数学中和生活中一些特殊表达方式和特殊关系式.
如a≥3是a>3或a=3;xy=0是x=0或y=0;x2+y2=0是x=0且y=0.指出下列命题的形式及构成它的简单命题:
(1)24既是8的倍数,也是6的倍数;
(2)菱形是圆的内接四边形或是圆的外切四边形.
[解析] (1)这个命题是“p∧q”的形式,其中p:24是8的倍数,q:24是6的倍数.
(2)这个命题是“p∨q”的形式,其中p:菱形是圆的内接四边形,q:菱形是圆的外切四边形.含有逻辑联结词的复合命题的写法 [分析] 由题目可获取以下主要信息:
①给定两个命题p、q.
②写出由它构成的含有逻辑联结词的复合命题.
解答这类题目的关键是要正确地使用联结词,并注意语法上的要求.
[方法规律总结] 用逻辑联结词“且”、“或”联结两个命题时,关键是正确理解这些词语的意义及在日常生活中的同义词,选择合适的联结词,有时为了语法的要求及语句的通顺也可进行适当的省略和变形.(1)分别写出由下列命题构成的“p或q”、“p且q”形式的复合命题,p:平行四边形的对角线相等;q:平行四边形的对角线互相平分.
(2)已知命题p:王茹是共青团员,q:王茹是三好学习,用自然语言表述命题p∧q,p∨q.
[解析] (1) p∧q:平行四边形的对角线相等且互相平分;
p∨q:平行四边形的对角线相等或互相平分.
(2)p∧q:王茹既是共青团员,又是三好学习;
p∨q:王茹是共青团员或是三好学生.[解析] (1)这个命题是“p∧q”的形式,其中p:48是16的倍数,是真命题;q:48是12的倍数,是真命题,所以“48是16与12的公倍数”是真命题.
(2)这个命题是“p∨q”的形式.其中p:相似三角形的周长相等,是假命题;q:相似三角形的对应角相等,是真命题,所以“相似三角形的周长相等或对应角相等”是真命题.含有逻辑联结词的命题真假的判断
[方法规律总结] 判断“p∧q”、“p∨q”形式复合命题真假的步骤:
第一步,确定复合命题的构成形式;
第二步,判断简单命题p、q的真假;
第三步,根据真值表作出判断.
注意:一真“或”为真,一假“且”为假.
指出下列各命题的构成形式并判断命题的真假.
(1)等腰三角形的顶角平分线垂直平分底边;
(2)方程x2-3x-4=0的根是-4或1.
[解析] (1)这一命题是“p∧q”的形式.
其中p:等腰三角形的顶角平分线垂直于底边,
q:等腰三角形的顶角平分线平分底边.
因为p、q都是真命题,所以这一复合命题是一个真命题.
(2)这一命题是“p∨q”的形式,
其中p:方程x2-3x-4=0的一个根是-4,
q:方程x2-3x-4=0的一个根是1,
因为p、q都是假命题,所以这一复合命题是一个假命题.求解含逻辑联结词命题中的参数 [解题思路探究] 第一步,审题:
审结论明确解题方向:“求实数m的取值范围”,应依据命题p∨q为真,p∧q为假建立关于m的不等式组求解.
审条件挖掘解题信息:由关于x的绝对值不等式|x-1|>m-1的解集为R,知m-1<0;由指数函数f(x)=(5-2x)x为增函数知5-2m>1;由“p∨q”为真,p∧q为假结合真值表可得p、q的真假.
第二步,探求条件与结论之间的联系,确定解题突破口和解答步骤,先求P为真时m的取值范围,再求q为真时m的取值范围,然后由复合命题真假确定简单命题p、q的真假,并求m的相应取值范围,最后下结论.
第三步,规范解答.[解析] 不等式|x-1|>m-1的解集为R,须m-1<0,即p是真命题时,m<1;
函数f(x)=(5-2m)x是R上的增函数,须5-2m>1,即q是真命题时,m<2.
∵p或q为真命题,p且q为假命题,
∴p、q中一个为真命题,另一个为假命题.
(1)当p真,q假时,m<1且m≥2,此时无解;
(2)当p假,q真时,m≥1且m<2,此时1≤m<2,
因此1≤m<2.
[点评] “p∧q”为真,则p真且q真;“p∧q”为假,则p、q至少一假;“p∨q”为真,则p、q至少一真;“p∨q”为假,则p、q都为假.
已知命题p:函数y=-x2+mx+1在(-1,+∞)上单调递减;命题q:函数y=mx2+x-1<0恒成立.若p∨q为真命题,p∧q为假命题,则m的取值范围是________.[辨析] 错解的原因是忽视了前提条件a>0.
[正解] ∵函数y=ax在R上单调递增,∴a>1,
∴p:a>1.
∵不等式x2-ax+1>0时x∈R恒成立,
∴Δ=a2-4=0,∴-2∴q:0
“且”与“或”第一章1.了解逻辑联结词“且”、“或”的意义,会用联结词“且”、“或”联结或改写某些数学命题,会判断命题“p且q”、“p或q”的真假.
2.能把文字语言,符号语言相互转化.重点:了解“且”与“或”的含义,能判定由“且”、“或”组成的新命题的真假.
难点:对“或”的含义的理解1.一般地,用联结词“且”把命题p和q联结起来,就得到一个新命题,记作________,读作________.
2.关于逻辑联结词“且”
(1)“且”的含义与日常语言中的“并且”、“及”、“和”相当,是连词“既……又……”的意思,二者须_______成立.逻辑联结词“且”新知导学 p∧qp且q同时(2)从如图所示串联开关电路上看,当两个开关S1、S2__________时,灯才能亮;当两个开关S1、S2中一个不闭合或两个都不闭合时,灯都不会亮.都闭合(3)从集合角度理解“且”即集合运算“______”.
设命题p:x∈A,命题q:x∈B,
则p∧q?x∈A,且x∈B?x∈(A∩B).
(4)“p∧q”是这样的一个复合命题:当p、q都是真命题时,p∧q是_____命题;当p、q两个命题中有一个命题是假命题时,p∧q是______命题.交真假
牛刀小试
1.“xy≠0”是指( )
A.x≠0且y≠0
B.x≠0或y≠0
C.x,y至少一个不为0
D.不都是0
[答案] A
[解析] xy≠0当且仅当x≠0且y≠0.2.p:点P在直线y=2x-3上;q:点P在曲线y=-x2上,则使“p∧q”为真命题的一个点P(x,y)是( )
A.(0,-3) B.(1,2)
C.(1,-1) D.(-1,1)
[答案] C3.一般地,用联结词“或”把命题p和q联结起来,就得到一个新命题,记作_______,读作________.
4.关于逻辑联结词“或”
(1)“或”的含义和日常语言中的“或者”相当.是“要么……要么……”的意义,二者中有________成立即可.
(2)从并联开关电路上看,当两个开关S1、S2至少有一个闭合时,灯就亮,只有当两个开关S1和S2__________时,灯才不会亮.逻辑联结词“或”新知导学 p∨qp或q一个都断开(3)从集合角度理解“或”即集合运算“_____”.
设命题p:x∈A,命题q:x∈B,
则p∨q?x∈A,或x∈B?x∈(A∪B).并(4)当p、q两个命题有一个命题是真命题时,p∨q是_____命题;当p、q两个命题都是假命题时,p∨q是______命题.
逻辑联结词“或”与自然语言中的“或者”、“可能”相当,但自然语言中的“或者”有两种用法:一是“不可兼”的“或”;二是“可兼”的“或”,而我们仅研究可兼“或”在数学中的含义.真假牛刀小试
3.下列判断正确的是( )
A.命题p为真命题,命题“p或q”不一定是真命题
B.命题“p且q”是真命题时,命题p一定是真命题
C.命题“p且q”是假命题,命题p一定是假命题
D.命题p是假命题,命题“p且q”不一定是假命题
[答案] B
[解析] 因为p、q都为真命题时,“p且q”为真命题.4.由下列各组命题构成的新命题“p或q”、“p且q”都为真命题的是( )
A.p:4+4=9,q:7>4
B.p:a∈{a,b,c},q:{a}?{a,b,c}
C.p:15是质数,q:8是12的约数
D.p:2是偶数,q:2不是质数
[答案] B
[解析] “p或q”“p且q”都为真,则p真q真,故选B.5.给出如下条件:
(1)“p成立,q不成立”;
(2)“p不成立,q成立”;
(3)“p与q都成立”;
(4)“p与q都不成立”.
其中能使“p或q”成立的是________(填序号).
[答案] (1)(2)(3)命题的构成形式 [分析] 本题考查命题的构成形式,是本节课的重点,也是以后学习的基础.
[解析] (1)这个命题是“p且q”的形式,其中,p:小李是老师;q:小赵是老师.
(2)这个命题是“p或q”的形式,其中,p:1是合数;q:1是质数.
(3)这个命题是“p且q”的形式,其中,p:他是运动员;q:他是教练员.
(4)这个命题是“p且q”的形式,其中,p:这些文学作品艺术上有缺点;q:这些文学作品政治上有错误.[方法规律总结] 1.辨别复合命题的构成形式时,应根据组成复合命题的语句中所出现的逻辑联结词,或语句的意义确定复合命题的形式.
2.准确理解语义应注意抓住一些关键词.如“是…也是…”“兼”,“不但…而且…”,“既…又…”,“要么…,要么…”,“不仅…还…”等.
3.要注意数学中和生活中一些特殊表达方式和特殊关系式.
如a≥3是a>3或a=3;xy=0是x=0或y=0;x2+y2=0是x=0且y=0.指出下列命题的形式及构成它的简单命题:
(1)24既是8的倍数,也是6的倍数;
(2)菱形是圆的内接四边形或是圆的外切四边形.
[解析] (1)这个命题是“p∧q”的形式,其中p:24是8的倍数,q:24是6的倍数.
(2)这个命题是“p∨q”的形式,其中p:菱形是圆的内接四边形,q:菱形是圆的外切四边形.含有逻辑联结词的复合命题的写法 [分析] 由题目可获取以下主要信息:
①给定两个命题p、q.
②写出由它构成的含有逻辑联结词的复合命题.
解答这类题目的关键是要正确地使用联结词,并注意语法上的要求.
[方法规律总结] 用逻辑联结词“且”、“或”联结两个命题时,关键是正确理解这些词语的意义及在日常生活中的同义词,选择合适的联结词,有时为了语法的要求及语句的通顺也可进行适当的省略和变形.(1)分别写出由下列命题构成的“p或q”、“p且q”形式的复合命题,p:平行四边形的对角线相等;q:平行四边形的对角线互相平分.
(2)已知命题p:王茹是共青团员,q:王茹是三好学习,用自然语言表述命题p∧q,p∨q.
[解析] (1) p∧q:平行四边形的对角线相等且互相平分;
p∨q:平行四边形的对角线相等或互相平分.
(2)p∧q:王茹既是共青团员,又是三好学习;
p∨q:王茹是共青团员或是三好学生.[解析] (1)这个命题是“p∧q”的形式,其中p:48是16的倍数,是真命题;q:48是12的倍数,是真命题,所以“48是16与12的公倍数”是真命题.
(2)这个命题是“p∨q”的形式.其中p:相似三角形的周长相等,是假命题;q:相似三角形的对应角相等,是真命题,所以“相似三角形的周长相等或对应角相等”是真命题.含有逻辑联结词的命题真假的判断
[方法规律总结] 判断“p∧q”、“p∨q”形式复合命题真假的步骤:
第一步,确定复合命题的构成形式;
第二步,判断简单命题p、q的真假;
第三步,根据真值表作出判断.
注意:一真“或”为真,一假“且”为假.
指出下列各命题的构成形式并判断命题的真假.
(1)等腰三角形的顶角平分线垂直平分底边;
(2)方程x2-3x-4=0的根是-4或1.
[解析] (1)这一命题是“p∧q”的形式.
其中p:等腰三角形的顶角平分线垂直于底边,
q:等腰三角形的顶角平分线平分底边.
因为p、q都是真命题,所以这一复合命题是一个真命题.
(2)这一命题是“p∨q”的形式,
其中p:方程x2-3x-4=0的一个根是-4,
q:方程x2-3x-4=0的一个根是1,
因为p、q都是假命题,所以这一复合命题是一个假命题.求解含逻辑联结词命题中的参数 [解题思路探究] 第一步,审题:
审结论明确解题方向:“求实数m的取值范围”,应依据命题p∨q为真,p∧q为假建立关于m的不等式组求解.
审条件挖掘解题信息:由关于x的绝对值不等式|x-1|>m-1的解集为R,知m-1<0;由指数函数f(x)=(5-2x)x为增函数知5-2m>1;由“p∨q”为真,p∧q为假结合真值表可得p、q的真假.
第二步,探求条件与结论之间的联系,确定解题突破口和解答步骤,先求P为真时m的取值范围,再求q为真时m的取值范围,然后由复合命题真假确定简单命题p、q的真假,并求m的相应取值范围,最后下结论.
第三步,规范解答.[解析] 不等式|x-1|>m-1的解集为R,须m-1<0,即p是真命题时,m<1;
函数f(x)=(5-2m)x是R上的增函数,须5-2m>1,即q是真命题时,m<2.
∵p或q为真命题,p且q为假命题,
∴p、q中一个为真命题,另一个为假命题.
(1)当p真,q假时,m<1且m≥2,此时无解;
(2)当p假,q真时,m≥1且m<2,此时1≤m<2,
因此1≤m<2.
[点评] “p∧q”为真,则p真且q真;“p∧q”为假,则p、q至少一假;“p∨q”为真,则p、q至少一真;“p∨q”为假,则p、q都为假.
已知命题p:函数y=-x2+mx+1在(-1,+∞)上单调递减;命题q:函数y=mx2+x-1<0恒成立.若p∨q为真命题,p∧q为假命题,则m的取值范围是________.[辨析] 错解的原因是忽视了前提条件a>0.
[正解] ∵函数y=ax在R上单调递增,∴a>1,
∴p:a>1.
∵不等式x2-ax+1>0时x∈R恒成立,
∴Δ=a2-4=0,∴-2
