2.1.1 椭圆及其标准方程 课件1
文档属性
| 名称 | 2.1.1 椭圆及其标准方程 课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 293.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-10 10:32:47 | ||
图片预览








文档简介
课件42张PPT。2.1.1 椭圆及其标准方程问题1:圆的定义是什么?圆的定义中有哪些条件? 1.一个定点
2.距离为定长回顾圆的定义:平面内与定点距离等于定长的点的集合(轨迹)圆C就是集合P={M| |MC|=r}这里定点为原点C,定长为半径r标准方程:以原点 C(0,0) 为圆心,r为半径探究
若适当改变上述两个条件(一个定点、定长),那么动点的轨迹又是什么呢?(2)把“一个定点”改为“两个定点F1和 F2”, 把“距离为定长”改为“距离相等”; (1)去掉“距离为定长”;(3)把一个定点改为两个定点F1和 F2 ,把距离为定长改为距离之比为2∶1; 答案是: 探究
若适当改变上述两个条件(一个定点、定长),那么动点的轨迹又是什么呢?(4)把一个定点改为两个定点F1和 F2 ,把距离为定长改为距离之和为定值; (5)把一个定点改为两个定点F1和F2 ,把距离为定长改为距离之差为定值;探究
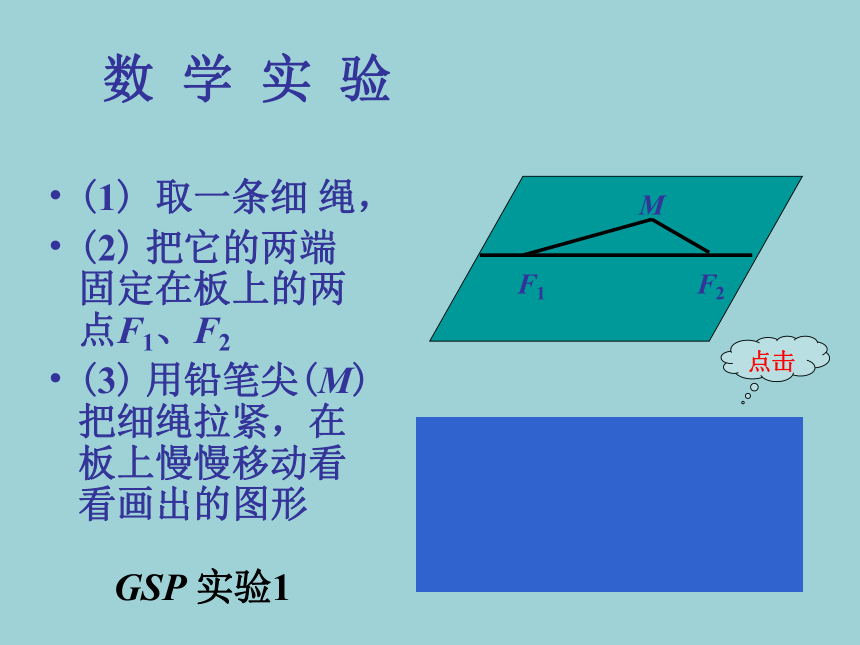
若适当改变上述两个条件(一个定点、定长),那么动点的轨迹又是什么呢?数 学 实 验(1) 取一条细 绳,
(2) 把它的两端 固定在板上的两点F1、F2
(3) 用铅笔尖(M)把细绳拉紧,在板上慢慢移动看看画出的图形GSP 实验1点击思考问题1:在作同一曲线图的过程中, 圆规两脚末端相对位置变没变?
2:在作图过程中绳子长度变没变?
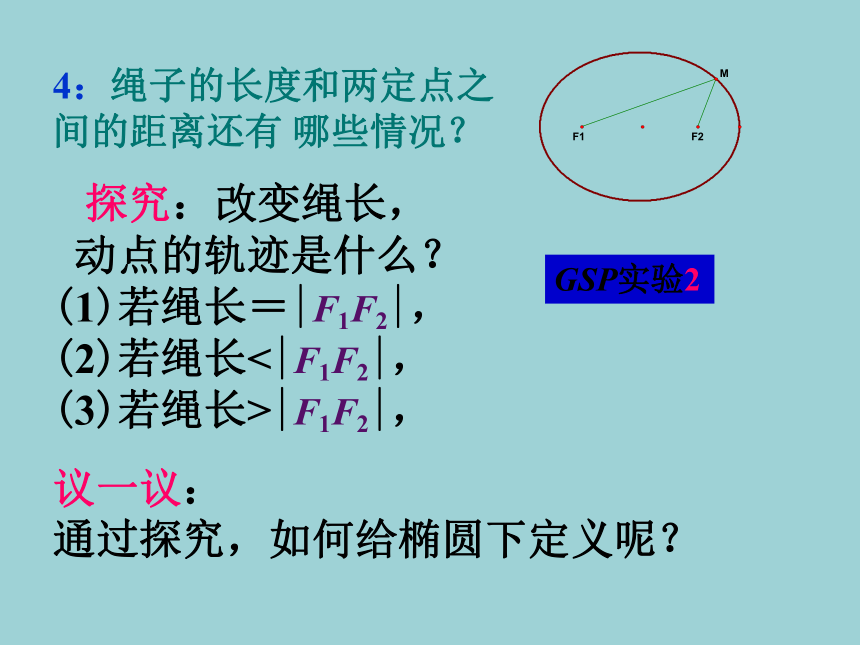
3:要使粉笔套上绳子时能移动,绳子长度与两定点距离大小关系怎样?4:绳子的长度和两定点之间的距离还有 哪些情况?议一议:
通过探究,如何给椭圆下定义呢? 探究:改变绳长,
动点的轨迹是什么?
(1)若绳长=|F1F2|,
(2)若绳长<|F1F2|,
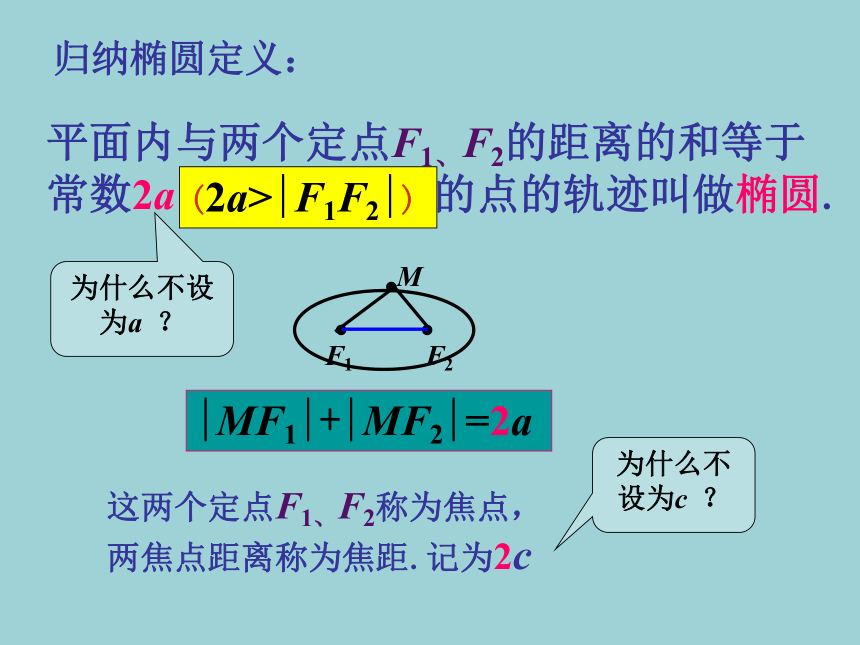
(3)若绳长>|F1F2|,GSP实验24:绳子的长度和两定点之间的距离还有 哪些情况?归纳椭圆定义:这两个定点F1、F2称为焦点,
两焦点距离称为焦距.记为2c平面内与两个定点F1、F2的距离的和等于常数2a 的点的轨迹叫做椭圆.(2a>|F1F2|)|MF1|+|MF2|=2a为什么不设为a ?为什么不设为c ?小结:满足几个条件 的动点的轨迹叫做椭圆?平面上----这是大前提
动点 M 到两个定点 F1、F2 的距离之和是常数 2a
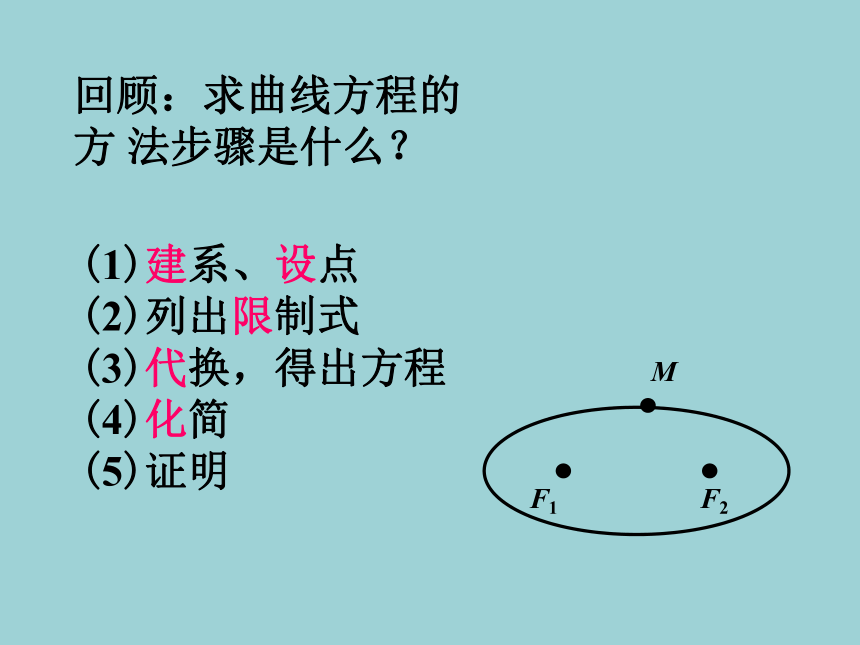
常数 2a 要大于焦距 2C(2a>2c)回顾:求曲线方程的方 法步骤是什么?(1)建系、设点
(2)列出限制式
(3)代换,得出方程
(4)化简
(5)证明回顾圆的定义:平面内与定点距离等于定长的点的集合(轨迹)圆C就是集合P={M| |MC|=r}这里定点为原点C,定长为半径r标准方程:以原点 C(0,0) 为圆心,r为半径如何建立坐标系?多种方案:1:建立坐标系.2:取定点F1为原点,F1, F2的连线为x轴,过F1与F1F2垂直的直线为y轴.3:取两定点的连线为x轴, F1F2的垂直平分线 为y轴.4:取两定点的连线为y轴, F1F2的垂直平分线 为x轴.F1F2MF1 (-c,0)、 F2 (c,0)|MF1|+|MF2|=2a|F1F2|=2c类比圆,建立坐标系为什么不设为c ?为什么不设为a ?写出等量关系设M(x,y)是椭圆上任一点,
椭圆的焦距为2c(c>0),那么焦点F1、F2的坐标分别是(-c,0),(c,0).又设M与F1和F2的距离的和等于常数2a.由椭圆定义,椭圆就是集合P={M∣∣MF1∣+∣MF2∣=2a}推导标准方程∵∣MF1∣=∣MF2∣=∵ [(x-c)2 + y2 ]-[ (x+c)2 + y2 ]=-4cx猜猜椭圆的标准方程的形式?猜想推导标准方程(1) 、 (2)是对偶形式,两者相加得两边平方,并整理得,(a2-c2)x2+a2y2=a2(a2-c2). (4)(5)未臻完美? 猜想推导标准方程 由椭圆定义:2a>2c>0,即a>c>0,
∴ a2-c2>0 ,
设b>0,令 a2-c2=b2, (6)
代入上式整理得:
(7)简单是真理的标志,
美丽为数学所蕴含. 猜想焦点F1(?c, 0)、F2(c, 0). c2=a2-b2.所谓椭圆的标准方程,一定是焦点在坐标轴上,且两焦点的中点为坐标原点.思考-猜测 焦点在y轴上的椭圆的标准方程与焦点在x轴上的椭圆的标准方程一样吗?有何不同?简单是真理的标志,
美丽为数学所蕴含. 两种形式说明:1表示的椭圆焦点在x轴上,焦点是
F1(-c,0)、F2(c,0),其中c2=a2-b2说明:2表示的椭圆焦点在y轴上,焦点是
F1(0,-c),F2(0,c),其中c2=a2-b2形式1:形式2:几点说明:①注意两者的异同,两者的对称转换(因为x与y地位对称,两者互换)
②两种形式中,总有a>b>0;
③椭圆焦点始终在分母大的轴上;
④a、b、c始终满足c2=a2-b2 ;
⑤遇到形如Ax2+By2=C,只要A、B、 C同号,就是椭圆方程 快速反应536432例1 已知a=4,b=3,求焦点在x轴上的椭圆的标准方程.口答:根据已知条件,求焦点在x轴上的椭圆的标准方程(1)a=5,b=4(2)a= ,b=2练习2根据已知条件,求焦点在x轴上的椭圆的标准方程.(2)a= ,c=2 应 用 举 例 [例2] 平面内两定点的距离是8,写出到这两定点的距离的和是10的点的轨迹方程.例2 平面内有两个定点的距离是8,写出到这两个定点的距离的和是10的点的轨迹方程.解:[1] 判断:(1)和是常数;(2)常数大于两个定点之间的距离.故点的轨迹是椭圆.[2] 取过两个定点的直线做 x 轴,它的线段垂直平分线做 y 轴,建立直角坐标系,从而保证方程是标准方程.[3] 根据已知求出a、c,再推出a、b写出椭圆的标准方程. [解] 这个轨迹是一个椭圆,两个定点是焦点,用F1、F2表示. 取过点F1和F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立直角坐标系.回归定义!例2 已知椭圆的焦点坐标是
F1(-4,0),F2(4,0),椭圆上的任意一点到F1、F2的距离之和是10,求椭圆的标准方程c=42a=10解:由已知得,c=4,2a=10例2 已知椭圆的焦点坐标是
F1(-4,0),F2(4,0),椭圆上的任意一点到F1、F2的距离之和是10,求椭圆的标准方程例3 椭圆的两个焦点分别是 (0,-2)、(0,2),并且椭圆经过点(-1.5,2.5). 求它的标准方程.. 例3 椭圆的两个焦点是(0,-2)、(0,2),且椭圆经过点(-1.5,2.5).求它的标准方程.解:因为椭圆的焦点在y轴上,所以设它的标准方程为由椭圆定义:∴a= ,c= , ∴b2=a2-c2= ∴所求椭圆的标准方程为26其它方法?待定系数法
方程思想勇攀高峰^_^小结 ------“定义法”
[1]根据椭圆定义判断点的轨迹是椭圆
[2]象推导椭圆的标准方程时一样,以焦点所在直线为一个坐标轴,以焦点所在线段的垂直平分线为另一坐标轴,建立直角坐标系.从而保证椭圆的方程是标准方程.
[3]设椭圆标准方程,即用待定系数法
[4]写出椭圆的标准方程 1.一个定义: 小 结2.两个方程:①②3.三个思想:①整体思想②数形结合③方程思想比较称为椭圆的标准方程焦点在x轴上,焦点是F1(-c,0)F2(c,0)焦点在y轴上,焦点是F1(0,-c)F2(0,c)如何判断焦点?所谓椭圆的标准方程,一定是焦点在坐标轴
上,且两焦点的中点为坐标原点.称为椭圆的标准方程如何求焦点?椭圆标准方程的焦点在分母大的那个轴上.标准方程图形焦点坐标定 义a b c
的关系焦点位置
的判断F1(- C, 0)F2(C, 0)F1( 0 ,- C)F2( 0 , C)分母哪个大,焦点就在哪个轴上.作业1.课本P53.1(写书上)
2.课本P53.2(1)(2)(3)在平面内进一步的探究: 与两个定点F1 , F2的距离的和
等于常数的点轨迹叫做椭圆(大于 )椭圆及其标准方程. .形状不变,大小改变,随常数的增大而大,随常数的减小而小.1、焦点不变常数变化时椭圆的变化情况:. .. .. . . .. .. . . . 2、常数不变焦点变化时椭圆的变化情况:形状改变,随焦距的减小越来越圆,随焦距的增大越来越椭.3、常数等于焦距时,轨迹是
.小于焦距时线段F1F2无轨迹.. .F1 F2.P1.P2.P3.P4
2.距离为定长回顾圆的定义:平面内与定点距离等于定长的点的集合(轨迹)圆C就是集合P={M| |MC|=r}这里定点为原点C,定长为半径r标准方程:以原点 C(0,0) 为圆心,r为半径探究
若适当改变上述两个条件(一个定点、定长),那么动点的轨迹又是什么呢?(2)把“一个定点”改为“两个定点F1和 F2”, 把“距离为定长”改为“距离相等”; (1)去掉“距离为定长”;(3)把一个定点改为两个定点F1和 F2 ,把距离为定长改为距离之比为2∶1; 答案是: 探究
若适当改变上述两个条件(一个定点、定长),那么动点的轨迹又是什么呢?(4)把一个定点改为两个定点F1和 F2 ,把距离为定长改为距离之和为定值; (5)把一个定点改为两个定点F1和F2 ,把距离为定长改为距离之差为定值;探究
若适当改变上述两个条件(一个定点、定长),那么动点的轨迹又是什么呢?数 学 实 验(1) 取一条细 绳,
(2) 把它的两端 固定在板上的两点F1、F2
(3) 用铅笔尖(M)把细绳拉紧,在板上慢慢移动看看画出的图形GSP 实验1点击思考问题1:在作同一曲线图的过程中, 圆规两脚末端相对位置变没变?
2:在作图过程中绳子长度变没变?
3:要使粉笔套上绳子时能移动,绳子长度与两定点距离大小关系怎样?4:绳子的长度和两定点之间的距离还有 哪些情况?议一议:
通过探究,如何给椭圆下定义呢? 探究:改变绳长,
动点的轨迹是什么?
(1)若绳长=|F1F2|,
(2)若绳长<|F1F2|,
(3)若绳长>|F1F2|,GSP实验24:绳子的长度和两定点之间的距离还有 哪些情况?归纳椭圆定义:这两个定点F1、F2称为焦点,
两焦点距离称为焦距.记为2c平面内与两个定点F1、F2的距离的和等于常数2a 的点的轨迹叫做椭圆.(2a>|F1F2|)|MF1|+|MF2|=2a为什么不设为a ?为什么不设为c ?小结:满足几个条件 的动点的轨迹叫做椭圆?平面上----这是大前提
动点 M 到两个定点 F1、F2 的距离之和是常数 2a
常数 2a 要大于焦距 2C(2a>2c)回顾:求曲线方程的方 法步骤是什么?(1)建系、设点
(2)列出限制式
(3)代换,得出方程
(4)化简
(5)证明回顾圆的定义:平面内与定点距离等于定长的点的集合(轨迹)圆C就是集合P={M| |MC|=r}这里定点为原点C,定长为半径r标准方程:以原点 C(0,0) 为圆心,r为半径如何建立坐标系?多种方案:1:建立坐标系.2:取定点F1为原点,F1, F2的连线为x轴,过F1与F1F2垂直的直线为y轴.3:取两定点的连线为x轴, F1F2的垂直平分线 为y轴.4:取两定点的连线为y轴, F1F2的垂直平分线 为x轴.F1F2MF1 (-c,0)、 F2 (c,0)|MF1|+|MF2|=2a|F1F2|=2c类比圆,建立坐标系为什么不设为c ?为什么不设为a ?写出等量关系设M(x,y)是椭圆上任一点,
椭圆的焦距为2c(c>0),那么焦点F1、F2的坐标分别是(-c,0),(c,0).又设M与F1和F2的距离的和等于常数2a.由椭圆定义,椭圆就是集合P={M∣∣MF1∣+∣MF2∣=2a}推导标准方程∵∣MF1∣=∣MF2∣=∵ [(x-c)2 + y2 ]-[ (x+c)2 + y2 ]=-4cx猜猜椭圆的标准方程的形式?猜想推导标准方程(1) 、 (2)是对偶形式,两者相加得两边平方,并整理得,(a2-c2)x2+a2y2=a2(a2-c2). (4)(5)未臻完美? 猜想推导标准方程 由椭圆定义:2a>2c>0,即a>c>0,
∴ a2-c2>0 ,
设b>0,令 a2-c2=b2, (6)
代入上式整理得:
(7)简单是真理的标志,
美丽为数学所蕴含. 猜想焦点F1(?c, 0)、F2(c, 0). c2=a2-b2.所谓椭圆的标准方程,一定是焦点在坐标轴上,且两焦点的中点为坐标原点.思考-猜测 焦点在y轴上的椭圆的标准方程与焦点在x轴上的椭圆的标准方程一样吗?有何不同?简单是真理的标志,
美丽为数学所蕴含. 两种形式说明:1表示的椭圆焦点在x轴上,焦点是
F1(-c,0)、F2(c,0),其中c2=a2-b2说明:2表示的椭圆焦点在y轴上,焦点是
F1(0,-c),F2(0,c),其中c2=a2-b2形式1:形式2:几点说明:①注意两者的异同,两者的对称转换(因为x与y地位对称,两者互换)
②两种形式中,总有a>b>0;
③椭圆焦点始终在分母大的轴上;
④a、b、c始终满足c2=a2-b2 ;
⑤遇到形如Ax2+By2=C,只要A、B、 C同号,就是椭圆方程 快速反应536432例1 已知a=4,b=3,求焦点在x轴上的椭圆的标准方程.口答:根据已知条件,求焦点在x轴上的椭圆的标准方程(1)a=5,b=4(2)a= ,b=2练习2根据已知条件,求焦点在x轴上的椭圆的标准方程.(2)a= ,c=2 应 用 举 例 [例2] 平面内两定点的距离是8,写出到这两定点的距离的和是10的点的轨迹方程.例2 平面内有两个定点的距离是8,写出到这两个定点的距离的和是10的点的轨迹方程.解:[1] 判断:(1)和是常数;(2)常数大于两个定点之间的距离.故点的轨迹是椭圆.[2] 取过两个定点的直线做 x 轴,它的线段垂直平分线做 y 轴,建立直角坐标系,从而保证方程是标准方程.[3] 根据已知求出a、c,再推出a、b写出椭圆的标准方程. [解] 这个轨迹是一个椭圆,两个定点是焦点,用F1、F2表示. 取过点F1和F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立直角坐标系.回归定义!例2 已知椭圆的焦点坐标是
F1(-4,0),F2(4,0),椭圆上的任意一点到F1、F2的距离之和是10,求椭圆的标准方程c=42a=10解:由已知得,c=4,2a=10例2 已知椭圆的焦点坐标是
F1(-4,0),F2(4,0),椭圆上的任意一点到F1、F2的距离之和是10,求椭圆的标准方程例3 椭圆的两个焦点分别是 (0,-2)、(0,2),并且椭圆经过点(-1.5,2.5). 求它的标准方程.. 例3 椭圆的两个焦点是(0,-2)、(0,2),且椭圆经过点(-1.5,2.5).求它的标准方程.解:因为椭圆的焦点在y轴上,所以设它的标准方程为由椭圆定义:∴a= ,c= , ∴b2=a2-c2= ∴所求椭圆的标准方程为26其它方法?待定系数法
方程思想勇攀高峰^_^小结 ------“定义法”
[1]根据椭圆定义判断点的轨迹是椭圆
[2]象推导椭圆的标准方程时一样,以焦点所在直线为一个坐标轴,以焦点所在线段的垂直平分线为另一坐标轴,建立直角坐标系.从而保证椭圆的方程是标准方程.
[3]设椭圆标准方程,即用待定系数法
[4]写出椭圆的标准方程 1.一个定义: 小 结2.两个方程:①②3.三个思想:①整体思想②数形结合③方程思想比较称为椭圆的标准方程焦点在x轴上,焦点是F1(-c,0)F2(c,0)焦点在y轴上,焦点是F1(0,-c)F2(0,c)如何判断焦点?所谓椭圆的标准方程,一定是焦点在坐标轴
上,且两焦点的中点为坐标原点.称为椭圆的标准方程如何求焦点?椭圆标准方程的焦点在分母大的那个轴上.标准方程图形焦点坐标定 义a b c
的关系焦点位置
的判断F1(- C, 0)F2(C, 0)F1( 0 ,- C)F2( 0 , C)分母哪个大,焦点就在哪个轴上.作业1.课本P53.1(写书上)
2.课本P53.2(1)(2)(3)在平面内进一步的探究: 与两个定点F1 , F2的距离的和
等于常数的点轨迹叫做椭圆(大于 )椭圆及其标准方程. .形状不变,大小改变,随常数的增大而大,随常数的减小而小.1、焦点不变常数变化时椭圆的变化情况:. .. .. . . .. .. . . . 2、常数不变焦点变化时椭圆的变化情况:形状改变,随焦距的减小越来越圆,随焦距的增大越来越椭.3、常数等于焦距时,轨迹是
.小于焦距时线段F1F2无轨迹.. .F1 F2.P1.P2.P3.P4
