2.1.2 椭圆的简单几何性质 课件1
文档属性
| 名称 | 2.1.2 椭圆的简单几何性质 课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 159.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-10 10:36:43 | ||
图片预览








文档简介
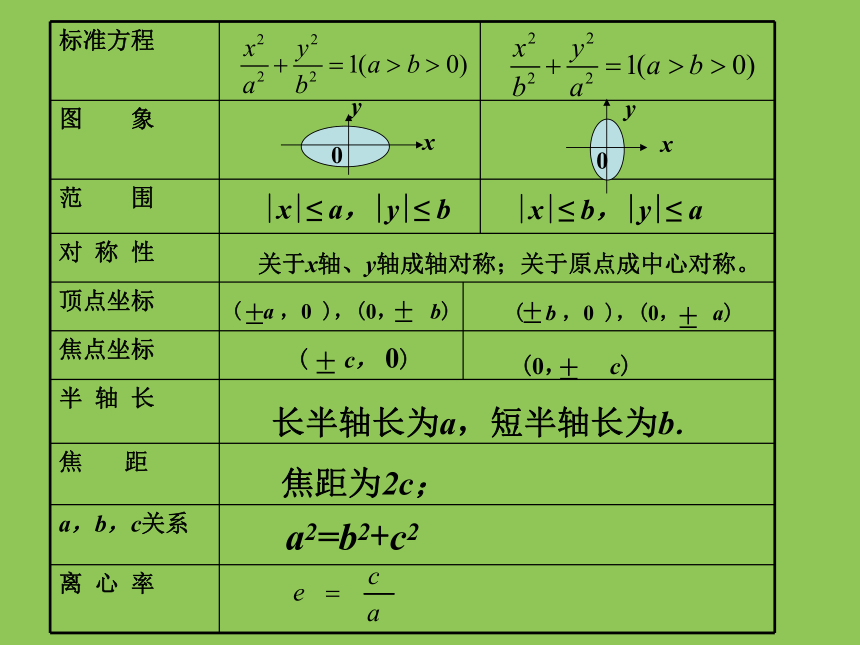
课件20张PPT。2.1.2椭圆的简单几何性质一、复习1.椭圆的定义:平面内与两个定点F1、F2的距离的和等于常数(大于|F1F2 |)的点的轨迹叫做椭圆。2.椭圆的标准方程是:3.椭圆中a,b,c的关系是:a2=b2+c2画出椭圆 的图形(草图)A1 B1 A2 B2 观察椭圆图形,你能发现椭圆有哪些特征?这些特征能否通过椭圆的方程来研究?几何性质1、范围(1)由图知:-a≤x≤a; -b≤y≤b(2)由方程:-a≤x≤a-b≤y≤b椭圆位于直线x=±a和直线y=±b围成的矩形区域内。以 为例2、对称性(1)由图知:关于x 、y轴成轴对称,关于原点成中心对称。(2)由方程:以-x代x
y不变以-y代y
x不变以-x代x
-y代y代入方程
仍成立f(x,y)=f(-x,y)f(x,y)=f(x, -y)f(x,y)=f(-x, -y)关于y轴对称关于x轴对称关于原点对称3、顶点(1)椭圆的顶点:椭圆与坐标轴的四个交点。顶点的坐标为:A1(-a,0)、A2(a ,0)
B1(0,-b)、B2(0,b)(2)长轴:线段A1A2
短轴:线段B1B2
长轴长:2a; 长半轴长:a
短轴长:2b; 短半轴长:b(3)六个特殊点:四个顶点, 两个焦点。短轴端点、中心、焦点构成一直角Δ,
且三边长为a,b,c椭圆的离心率2.范围:因为a>c>0,所以0 e越接近1,椭圆越扁;反之,e越接近0,椭圆越圆.
1.定义:椭圆的焦距与长轴长的比,即
叫做椭圆的离心率.|x|≤ a,|y|≤ b|x|≤ b,|y|≤ a关于x轴、y轴成轴对称;关于原点成中心对称。( a ,0 ),(0, b)( b ,0 ),(0, a)( c, 0)(0, c)长半轴长为a,短半轴长为b.焦距为2c;a2=b2+c2例1.已知椭圆方程为16x2+25y2=400,它的长轴长是: 。短轴长是: 。
焦距是: 。 离心率等于: 。
焦点坐标是: 。顶点坐标是: 。
外切矩形的面积等于: 。 108680题型一、椭圆的几何性质的简单应用题型一、椭圆的几何性质的简单应用例2.求适合下列条件的椭圆的标准方程:
(1)焦点在x轴上,a=6, ;
(2)焦点在x轴上,c=6, .题型一、椭圆的几何性质的简单应用题型二、求椭圆的离心率练习:已知F1为椭圆的左焦点,A、B分别为椭圆的右顶点和上顶点,P为椭圆上的点,当PF1⊥F1A,PO∥AB(O为椭圆的中心)时,求椭圆的离心率.题型二、求椭圆的离心率题型二、求椭圆的离心率椭圆的第二定义例6P41动点M(x,y)与定点F(4,0)的距离和它到定直线l : 的距离的比是常数 ,求动点M的轨迹.椭圆的第二定义练习:
动点M(x,y)与定点F(c,0)的距离和它到定直线l : 的距离的比是常数 (a>c>0) ,求动点M的轨迹.椭圆的第二定义练习:
动点M(x,y)与定点F(c,0)的距离和它到定直线l : 的距离的比是常数 (a>c>0) ,求动点M的轨迹.椭圆的第二定义 平面内到一个定点F的距离和它到定直线l 的距离之比是常数 的点的轨迹是椭圆,定点F是椭圆的焦点,定直线l 是椭圆的准线,e是椭圆的离心率.椭圆的第二定义练习
设F1、F2是椭圆的左、右焦点,若在其右准线上存在点P,使PF1的中垂线经过点F2 ,则椭圆的离心率的取值范围为椭圆的第二定义练习
在给定椭圆中,过焦点且垂直于长轴的弦长为 ,焦点到相应的准线的距离为1,则椭圆的离心率为
y不变以-y代y
x不变以-x代x
-y代y代入方程
仍成立f(x,y)=f(-x,y)f(x,y)=f(x, -y)f(x,y)=f(-x, -y)关于y轴对称关于x轴对称关于原点对称3、顶点(1)椭圆的顶点:椭圆与坐标轴的四个交点。顶点的坐标为:A1(-a,0)、A2(a ,0)
B1(0,-b)、B2(0,b)(2)长轴:线段A1A2
短轴:线段B1B2
长轴长:2a; 长半轴长:a
短轴长:2b; 短半轴长:b(3)六个特殊点:四个顶点, 两个焦点。短轴端点、中心、焦点构成一直角Δ,
且三边长为a,b,c椭圆的离心率2.范围:因为a>c>0,所以0
1.定义:椭圆的焦距与长轴长的比,即
叫做椭圆的离心率.|x|≤ a,|y|≤ b|x|≤ b,|y|≤ a关于x轴、y轴成轴对称;关于原点成中心对称。( a ,0 ),(0, b)( b ,0 ),(0, a)( c, 0)(0, c)长半轴长为a,短半轴长为b.焦距为2c;a2=b2+c2例1.已知椭圆方程为16x2+25y2=400,它的长轴长是: 。短轴长是: 。
焦距是: 。 离心率等于: 。
焦点坐标是: 。顶点坐标是: 。
外切矩形的面积等于: 。 108680题型一、椭圆的几何性质的简单应用题型一、椭圆的几何性质的简单应用例2.求适合下列条件的椭圆的标准方程:
(1)焦点在x轴上,a=6, ;
(2)焦点在x轴上,c=6, .题型一、椭圆的几何性质的简单应用题型二、求椭圆的离心率练习:已知F1为椭圆的左焦点,A、B分别为椭圆的右顶点和上顶点,P为椭圆上的点,当PF1⊥F1A,PO∥AB(O为椭圆的中心)时,求椭圆的离心率.题型二、求椭圆的离心率题型二、求椭圆的离心率椭圆的第二定义例6P41动点M(x,y)与定点F(4,0)的距离和它到定直线l : 的距离的比是常数 ,求动点M的轨迹.椭圆的第二定义练习:
动点M(x,y)与定点F(c,0)的距离和它到定直线l : 的距离的比是常数 (a>c>0) ,求动点M的轨迹.椭圆的第二定义练习:
动点M(x,y)与定点F(c,0)的距离和它到定直线l : 的距离的比是常数 (a>c>0) ,求动点M的轨迹.椭圆的第二定义 平面内到一个定点F的距离和它到定直线l 的距离之比是常数 的点的轨迹是椭圆,定点F是椭圆的焦点,定直线l 是椭圆的准线,e是椭圆的离心率.椭圆的第二定义练习
设F1、F2是椭圆的左、右焦点,若在其右准线上存在点P,使PF1的中垂线经过点F2 ,则椭圆的离心率的取值范围为椭圆的第二定义练习
在给定椭圆中,过焦点且垂直于长轴的弦长为 ,焦点到相应的准线的距离为1,则椭圆的离心率为
